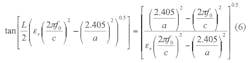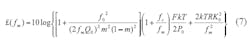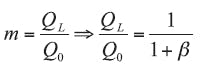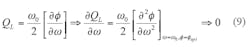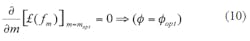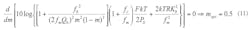Phase noise can be a limiting factor in modern communications systems, especially those that rely on phase-based modulation. Phase noise can increase the bit error rate (BER) of a telecommunications link, in addition to degrading both the stability of beams in particle accelerators and the sensitivity of radar systems. Fortunately, when properly designed, dielectric resonator oscillators (DROs) can deliver stable signals at microwave through millimeter-wave frequencies with excellent phase-noise characteristics. In particular, a new line of compact DROs from Synergy Microwave Corp. features low phase-noise levels at fundamental-frequency outputs through 10 GHz and higher, for use in commercial, industrial, and military applications (Fig. 1).
1. This photograph shows an actual 10-GHz DRO circuit and its housing.
The high quality factor (Q) of a dielectric resonator makes it possible to achieve oscillators with excellent phase-noise performance at microwave and millimeter wave frequencies. Dielectric resonators are fabricated on ceramic materials with high dielectric permittivity, high Q, and high temperature stability. They have much smaller size compared to cavity resonators; therefore, they are frequently employed in the design of frequency stable RF circuits (especially in oscillators).
When high data rates must be transferred—as with multiple-quadrature amplitude modulation (M-QAM) schemes in Long-Term-Evolution (LTE), local multipoint distribution service (LMDS), and fixed-frequency point-to-point digital radios and satellite-communications (satcom) links—such systems rely on free-running or phase-locked signal sources with low phase noise. Such spectrally pure sources are also invaluable for radar systems and in research laboratories. A wide range of military, industrial, medical, and test-and-measurement markets demand stable frequency sources with low phase-noise performance and low thermal drift. DROs have provided low-noise solutions in the frequency range from 3 to 18 GHz, with spectral purity that compares favorably to other competing solutions (such as multiplied lower frequency fundamental sources).
A typical DRO circuit uses high-Q dielectric resonator (DR) and active device in a series/parallel feedback configuration to achieve the negative resistance required for stable oscillations. The DR is typically a piece of a dielectric material, usually manufactured in a circular shape such as a disk or cylinder. It boasts very high (much higher than 1) relative dielectric constant, εr, that acts like a resonant cavity by means of reflections at the dielectric/air interface. The DR can resonate in a number of modes and frequencies depending on the type of material, dimensions, and the proximity and shapes of enclosures.
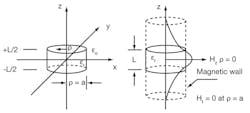
2. These diagrams show a typical disk dielectric-resonator TE01δ mode (left) and Hz field distribution (right).
Figure 2 shows a typical DR in a polar coordinate system used for providing insight into possible resonant conditions for a given physical dimension. These include L, the length of the DR, and a, the radius of the DR. It can be shown that by matching the tangential fields at the resonator (dielectric/air) interface, at | z | = L/2 it is possible to derive Eqs. 1 and 2:
Acos(βL/2) = Be–α(L/2) (1)
and
-(jA/Zd)sin(βL/2) = (B/Za)e–α(L/2) (2)
with:
Zd = ωμ0/α, (where Zd is the wave impedance within the dielectric) (3)
Za = jωμ0/α, (where Za is the wave impedance within the air) (4)
where α and β are the imaginary and real propagation constants, respectively. From Eqs. 1 and 2,
-jZa sin(βL/2) = ZdCOS(βL/2) → tan(βL/2) = α/β (5)
By solving transcendental Eq. 5, the resonant frequency, f0, the length, L, and the radius, a, of the DR are found by Eq. 6:
where:
L = the length of the DR;
a = the radius;
εr = the relative permittivity of the dielectric material; and
c = the speed of light in a vacuum.
Transcendental equation Eq. 6 produces two possible solutions for the resonant wavelength, λ, but only one is valid in yielding a deterministic solution within the dielectric (λεr) and the air (λεo).
Designing and fabricating low-noise-noise oscillator circuits based on DRs is not trivial, given the nonlinear natures of the active devices needed for the oscillators as well as the resonators. Synergy Microwave Corp. has studied the nonlinear behavior of these two key components for DROs and has developed a new line of low-noise DROs with outstanding phase-noise characteristics. These include the model DRO1000-8, which offers mechanical and electrical frequency tuning around a center frequency of 10 GHz.
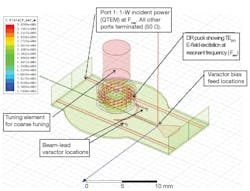
Figure 3 shows a typical block diagram of the 10-GHz DRO. One of the design challenges for this source involved maintaining low phase noise even with electronic varactor tuning, while also minimizing the cost of the oscillator by achieving a structure that could be assembled repeatably in production. To achieve this consistency in design and manufacturing, computer-aided-engineering (CAE) simulation tools were used, such as ANSYS HFSS from ANSYS and ADS Momentum software from Agilent Technologies.
3. This simple block diagram shows the basic components of a dielectric resonator oscillator.
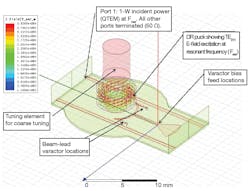
Figure 4 shows a three-dimensional (3D) model for the varactor-tuned DRO. The complete DRO design was evaluated and optimized using harmonic-balance circuit simulation along with electromagnetic (EM) co-simulation. This approach allows designers to achieve a optimum dynamic loaded Q-factor for a typical DR coupling arrangement in conjunction with the oscillator core, which is one of the preconditions for achieving lowest phase noise. The active device has been selected carefully with respect to noise figure and flicker noise, with optimum bias level conditions.
4. This is a three-dimensional (3D) model for a varactor-tuned dielectric resonator oscillator.
Equation 7 provides an expression for an oscillator or other source’s phase noise (see ref. 1):
where :
m = the ratio of the loaded and unloaded Q.
The coupling coefficient, β, and the ratio parameter m can be described by Eq. 8 as:
Dynamic loaded Q can be given by Eq. 9:
For maximum dynamic loaded Q, (∂/∂ω)[QL(ω)]ω = ω0 → 0, therefore, the minimum phase noise can be found by differentiating Eq. 7 with respect to ratio parameter m, and equating to zero for a minimum value of phase noise as shown in the next several equations:
where:
£(fm) = the ratio of the sideband power in a 1-Hz bandwidth at fm to total power in dB;
fm = the sideband frequency;
f0 = the offset frequency;
fc = the flicker corner frequency;
QL = the loaded quality factor;
Q0 = the unloaded quality factor;
F = the noise factor;
k = Boltzman’s constant;
T = the temperature (in degrees Kelvin);
P0 = the average output power;
R = the equivalent noise resistance of the tuning diode; and
K0 = the voltage gain.
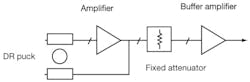
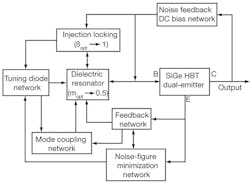
From Eq. 12 for low-phase-noise applications, mopt and βopt should be dynamically controlled and must lie in the vicinity of 0.5(mopt ≈ 0.5) and 1 (βopt ≈ 1), respectively, for the best phase-noise performance. Figure 5 shows a typical block diagram of the DRO circuit used for validating the approach of achieving minimum phase noise performances.
5. This block diagram shows some of the typical components in a dielectric-resonator-oscillator (DRO) circuit.
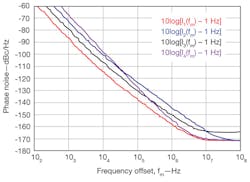
Figure 6 illustrates the impact of possible impairments on the phase noise performance. The red trace identifies the measured phase noise performance of Synergy’s new 10 GHz model number DRO100-8. The blue trace corresponds to a lower QL with identical oscillator core noise properties. The black and magenta traces correspond to identical QL but significantly higher effective noise figure or flicker corner frequency when the active device is not selected or biased optimally. A combination of these impairments together with nonlinear noise effects account for the much higher phase noise performance found in many competing DRO designs.
6. These plots show how various parameters, such as loaded resonator quality factor (Q), can impact the phase-noise performance of a microwave DRO.
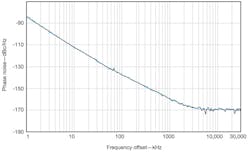
The model DRO100-8 DRO has a typical noise floor of –170 dBc/Hz, approaching state-of-the-art performance. The measured phase noise is –112 dBc/Hz offset 10 kHz from the carrier (Fig. 7). Mechanical and electrical tuning is available for frequency adjustment and phase locking. The frequency is set at the factory to 10 GHz and can be mechanically varied by approximately ±50 MHz. Tuning voltages of 1 to 15 VDC enable variations in the center frequency by ±1 MHz to compensate for frequency drift in phase-locked systems. The DRO features temperature stability of typically better than 80 ppm. The oscillator’s internal voltage regulation provides high immunity to power supply noise. It handles supply-voltage variations between +7 and +10 VDC with typically supply current of 50 mA and a specified operating temperature range of -25 to +70°C. The oscillator delivers +8 dBm or higher output power in a package measuring approximately 3.1 x 1.34 x 0.788 in., including its mounting flaps.
7. This is an actual phase-noise plot for a model 100-8 10-GHz DRO, made on an RF/microwave FSUP signal analyzer from Rohde & Schwarz.
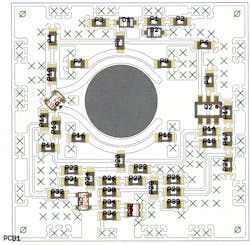
A number of variations in the DRO circuit were developed for applications that may require smaller units than the initial model. For example, the design team developed a prototype measuring just 0.75 x 0.85 in., as well as a surface-mount-device (SMD) version measuring just 0.50 x 0.50 in. Although these oscillators were developed for use at 10 GHz, they are not limited to that frequency; they can be designed for any fixed frequency from 3 to 18 GHz without long development lead times. As an example, Fig. 8 shows a prototype 10-GHz DRO layout for a 0.75 x 0.75 in. package. The measured phase-noise performance is better than -100 dBc/Hz offset 10 kHz from the carrier.
8. This is the typical layout for a 10-GHz DRO in a square housing measuring 0.5 x 0.5 in.
As with crystal oscillators, DROs can be prone to vibrational noise since the DR cannot be fully mechanically secured. To minimize such noise, vibrations must be damped before they reach the DR. The DRO100 features rugged construction with extensive damping of the DR to minimize vibration noise and microphonic effects, thus preventing unwanted modulation. The DRO’s low phase noise makes it well suited for use in high-data-rate communications systems; as reference oscillators for phase-noise-measurement systems; in radar, cable-television (CATV), optical SDH/SONET communications, and satcom systems; and in a variety of other high-frequency electronic systems requiring low-noise sources. Custom frequencies and packages (hermetic) can be developed on request.
Ulrich L. Rohde, Chairman
Ajay K. Poddar, Chief Scientist
Synergy Microwave Corp., 201 McLean Blvd., Paterson, NJ 07504; (973) 881-8000, FAX: (973) 881-8361, e-mail: [email protected], www.synergymwave.com.
Reference
1. U.L. Rohde, A.K. Poddar, and G. Boeck, Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, John Wiley & Sons Inc., 2005.