Microwave filters conventionally reflect electromagnetic (EM) waves from the load back to the source. In some cases, however, it is desirable to separate the reflected wave from the input, to protect the source from excessive power levels, for example. For this reason, absorptive filters have been developed to minimize reflections.1
Figure 1 shows the basic configuration of an absorptive filter. This type of filter is useful not only as an absorption filter, but also works as power combiner or diplexer. When there is only one signal input (port 1), port 2 is an absorption port and port 3 is an isolated port. Port 4 is the output port. When different input signals are applied at port 1 and port 3, the configuration can also work as a signal combiner. Recently, the substrate-integrated-waveguide (SIW) technique2,3 has been proposed in waveguide applications for microwave and millimeter-wave systems. SIW is made of various metallic via arrays in the substrate. Standard printed-circuit boards (PCBs) or low-temperature-cofired-ceramic (LTCC) substrates have been used to fabricate SIW devices. SIW technology has some advantages, such as high quality factor (Q), low insertion loss, reduced size, low cost, and easy integration with planar circuits. As a result, SIW technology is widely applied to all kinds of different filters4-6 and diplexer designs.7
In this article, a new class of cross-coupled absorption filter has been developed based on the SIW technique. It has sharp selectivity and high Q, and is easily integrated with planar circuits. The 3-dB hybrid coupler with two steps developed in this report differs from work published earlier.8 This 3-dB hybrid coupler exhibits good performance of power distribution. An absorption filter was fabricated with standard PCB boards, and a comparison of measured data with simulation results shows close agreement. It is apparent that SIW to air-filled waveguide transitions could be adopted to improve the power capacity and reduce the insertion loss compared to SIW-microstrip transitions.
Absorption filters are often used to separate reflected EM waves from an input signal port to protect the port from signal overload, for example. The structure of an absorption filter (Fig. 1) can also be used in other applications. The two filters in Fig.1 are identical.
In principle, when an EM wave is applied to port I (Fig. 2), only output signals result at port III. Ports II and IV are isolated from port I. When signals are reflected by the filters, they are all collected at Port II (Fig. 3) while the input and reflection signals are isolated at Port I.
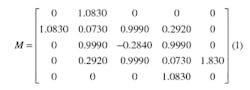
Atia and Williams9 first developed the coupling matrix synthesis methods of generalized Chebyshev filters for symmetric filter responses. Amari10,11 developed gradient-based optimization methods to synthesize the coupling matrix of a generalized Chebyshev filter. The coupling matrix of the filter presented here was extracted by means of gradient-based methods. The third-order filter has a center frequency of 11900 MHz and return loss of 22 dB. The bandwidth is 220 MHz. A finite transmission zero is positioned at 11800 MHz. The coupling matrix and frequency responses are shown in Fig. 4. In some cases, negative coupling occurs for the coupling matrix. Rosenberg12 proposed that the negative coupling could be accomplished by using the transformation properties of higher-order cavity modes (e.g., TE102) with H-plane coupling windows.
The dimensions of the coupling windows were obtained by simulations according to the normalized coupling matrix shown in the matrix of Eq. 1. Note that the resonating frequencies are not the same because of asymmetric frequency responses. Computation equations for the coupling coefficients by simulation are given by Eq. 213:
where:
f0i = the resonating frequency of a resonator without coupling windows and
fpi = the resonating frequency of a resonator with coupling windows, and i = 1, 2.
Simulation software was used to determine the initial dimensions of the filter, and the size of the SIW cavity was determined by the corresponding resonance frequency from ref. 14 for the TE101 dominant mode:
where:
weff = the equivalent width of the SIW cavity and leff = the equivalent length of the SIW cavity. They are expressed by15,16:
where:
w = the actual width of the SIW cavity,
l = the actual length of the SIW cavity,
d = the diameter of the metallic via holes,
p = the distance between adjacent metallic via holes,
c = the speed of light in free space,
mr = the relative permeability of the substrate, and
er = the relative permittivity of the substrate.
For the TE102 mode, the length of cavity is double of that of TE101 mode. The equation (4) is also applied to determine the equivalent length and width of TE102 mode cavities.
The absorption filter was designed by a combination of two identical filters and two identical 3-dB hybrid couplers. Figure 5 shows the frequency response of one of the 3-dB hybrid couplers. The return losses of port 1 and port 2 are better than 22 dB from 10.8 to 11.8 GHz.
Figure 6 shows the dimensions of one of the 3-dB hybrid couplers. An optimization procedure was needed for direct integration of the individual filters and hybrid couplers to achieve good performance.
Continued on page 2
Page Title
In the process of performing the simulation optimization, the radius of the metallic hole does not change. Only the distance of between the centers of the two metallic holes can be changed. The absorption filter was first optimized by the mode matching method developed by the current research group when the absorption filter was constructed with equivalent substrate waveguide and not with metallic holes. Then, after applying the length and width transformations of Eq. 4, the overall structure with metallic holes was optimized by means of the High-Frequency Structure Simulator (HFSS) EM software from Ansoft Corp. (www.ansoft.com) to eliminate the influence of metallic holes.
Figure 6 presents the configuration for a proposed cross-coupled SIW absorption filter with the physical parameters shown after some optimizations. The diameter of the metallic hole is 0.5 mm without any change. The minimal distance of between the edges of the two metallic holes is 0.8 mm. All dimensions are the distances between the centers of metallic holes.
The cross-coupled SIW absorptive filter was fabricated by using standard PCB processes. It was characterized without an further tuning. It was produced on RT/Duroid 5880 substrate material from Rogers Corp. (www.rogerscorporation.com) (Fig. 7). The substrate has a relative permittivity constant of 2.2 with 0.254 thickness and loss tangent (δ) of 0.0009. A SIW-microstrip tapered transition was designed with broadband response with return loss of better than 20 dB. Figure 6 shows the dimensions of the SIW-microstrip structure. Figure 8 offers a comparison between simulated and measured results, with good agreement between the two sets of data. Values for passband return loss are all better than 20 dB. The absorption levels of the reflected signals for port 1 are less than 17 dB from 10.80 to 11.65 GHz. Pass-band insertion loss is about 5.8 dB.
Compared to a conventional filter, the insertion loss appears poor because it has twice as many filters and losses from the other ports. The losses of the SMA and SIW-microstrip transitions are also included in the total. The above rejection band exhibits sharp frequency selectivity. The SIW-to-air-filled-rectangular-waveguide transitions17 can be adopted to reduce the insertion loss and improve the power capacity in place of the SIW-microstrip transitions.
The cross-coupled SIW absorption filter presented in this article features the sharp selectivity of a cross-coupled filter with the small size, low cost, and high Q associated with an SIW design. By following the design guidelines presented here, it is possible to create a custom filter that delivers similar benefits.
References
1. R.J. White and Michael F. Violette. Electromagnetic Compatibility Handbook, Van Nostrand Reinhold Co., New York, 1987.
2. A.J. Pilote, K.A. Leahy, B.A. Flanik, and K.A. Zaki, "Waveguide filters having a layered dielectric structure," U.A. Patent, No. 5382931, January 1995.
3. H. Uchimura, T. Takenoshita, and M. Fuji, "Development of a lamined waveguide," IEEE Transactions on Microwave Theory & Techniques, Vol. 46, pp. 2438-2443, December 1998.
4. Zhang-Cheng Hao, Wei Hong, Ji-Xin Chen, Xiao-Ping Chen, and Ke Wu, "Compact super-wide bandpass substrate integrated waveguide (SIW) filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 9, pp. 2968-2977, September 2005.
5. Xiaoping Chen, Wei Hong, Cui, T., Jixin Chen, and Ke Wu, "Substrate integrated waveguide (SIW) linear phase filter," IEEE Microwave and Wireless Components Letters, Vol. 15, pp. 787-789, November 2005.
6. Zhang Cheng Hao, Wei Hong, Xiao Ping Chen, Ji Xin Chen, Ke Wu, and Tie Jun Cui, "Multilayered substrate integrated waveguide (MSIW) elliptic filter," IEEE Microwave and Wireless Components Letters, Vol. 15, No. 2, pp. 95-97, February 2005.
7. Z.C. Hao, W. Hong, J.X. Chen, X.P. Chen, and K. Wu, "Planar diplexer for microwave integrated circuits," IEEE Proceedings on Microwave Antennas & Propagation, Vol. 152, No. 6, pp. 455-459, December 2005.
8. Z.C. Hao, W. Hong, J.X. Chen, X.P. Chen, and K. Wu, "Single-layer substrate integrated waveguide directional couplers," IEEE Proceedings on Microwave Antennas & Propagation, Vol. 153, No. 5, pp. 426-431, October 2006.
9. A.E. Atia and A.E. Williams. "New type of waveguide bandpass filters for satellite transponders," COMSAT Technology, Vol. 1, pp. 21-43, 1971.
10. S. Amari, "Synthesis of cross-coupled resonator filters using an analytical gradient-based optimization technique," IEEE Transactions on Microwave Theory & Techniques, Vol. 48, No. 9, pp. 1559–1564, September 2000.
11. S. Amari, Uwe. Rosenberg, and Jens Bornemann. "Adaptive synthesis and design of resonator filters with source/load-multiresonator coupling," IEEE Transactions on Microwave Theory & Techniques, Vol. 50, No. 8, pp. 1969-1977, August 2002.
12. U. Rosenberg, "New planar waveguide cavity elliptic function filters," in Proceedings of the 25th European Microwave Conference, Bologna, Italy, September 1995, pp. 524–527.
13. J.G. Hong, M.J. Lancaster, Microstrip Filters for RF/Microwave Applications. New York: Wiley-Interscience, 2000.
14. J.R. Bray and L. Roy, "Resonant frequencies of post-wall waveguide cavities," Proceedings of the Institute of Electronics Engineers, Vol. 150, No.10, pp. 365-268, October 2003.
15. F. Xu, Y. Zhang, W. Hong, K. Wu, and T.J. Cui, "Finite-difference frequency-domain algorithm for modeling guided-wave properties of substrate integrated waveguide," IEEE Transactions on Microwave Theory & Techniques, Vol. 51, No. 11, pp. 2221–2227, November 2003.
16. L. Yan, and W. Hong, "Investigations on the propagation characteristics of the substrate integrated waveguide based on the method of lines," IEEE Proceedings on Microwave Antennas & Propagation, 152, No. 1, pp. 35–42, 2005
17. Lei Xia, Ruiming Xu, Bo Yan, Jianlin Li, Yunchuan Guo, and Jianpeng Wang, "Broadband transition between air-filled waveguide and substrate integrated waveguide," IEE Electronics Letters, Vol. 42, No. 24, pp. 1403-1405, 2006.