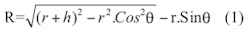Spherical Phased Array Links Remote Sensors
Remote sensing satellites must handle large amounts of data and thus transmit at high data rates. Because of this, the antenna design is critical for these satellites. Spherical phasedarray antennas can provide a workable solution for this application, with consistently high data-rate performance across the full distance of the satellite's coverage area. The effectiveness of the approach will be shown with an X-band design.
Spectrally efficient modulation is critical to a satellite- based remote sensing system,1-3 and quadraturephase- shift-keying (QPSK) modulation has generally been applied for high-datarate transmissions at Xband frequencies. To make optimum use of available power from the satellite, special antennas are required. For example, when a satellite is visible to the ground station, the path loss depends on the elevation angle of the ground station. Typically, isoflux antennas, which ensure near-constant signal strength at the receiving station when the satellite is traveling through the visible portion of its orbit, are often used on remote sensing satellites.4,5
The range of a satellite in a circular orbit (Fig. 1) can be computed from Eq. 1.
where
r = the earth's radius (6380 km),
h = the satellite's orbital height,
θ = ground antenna elevation, and
α = the angle between the axis of the antenna and the direction of the earth station.
The visibility or "look angle" is computed as 66.10 deg. from triangle OAS shown in Fig. 1 where AGO is the axis of the antenna looking at the earth, OG is the earth's radius, and GA is the satellite's orbital height (600 km).
The range of a satellite in an orbit from an antenna at ground station S varies from 2831 km (SA or SB in Fig. 1) when satellite is at point A and B corresponding to 0 and 180 deg. ground antenna elevation to 600 km when the satellite is overhead at point C. From this, the path loss can be computed according to (4 r/λ)2 at a carrier frequency of 8300 MHz The path loss was found to vary in level from 179.9 to 166.4 dB (Fig. 2). The signal received at the ground station, when the satellite transmits with a constant-gain antenna, increases by about 13.5 dB for ground-station elevation angles from 0 to 90 deg.
For isoflux antennas for onboard satellite use, the antenna radiation (gain) pattern is shaped to compensate for path-loss variations (Fig. 2). The gain at a 66-deg. look angle for the onboard antenna in an X-band remotesensing system can be increased by decreasing the gain at a 0-deg. angle so that the gain pattern matches the path-loss pattern over the range of elevation angles. The gain at 66 deg. was measured as +7 dBi, with a gain pattern nearly equivalent to the system's path-loss pattern, which is typical for a shaped-beam antenna.
With this antenna, the received signal strength at the ground station is nearly constant. But due to low gain of only +7 dBi at the maximum range angle, to maintain the required effective isotropic radiated power (EIRP), high onboard RF power must be available to transmit at high data rates. Typically about 40 W RF power is needed onboard the remote sensing satellite for a data rate of 105 MB/s. Such an isoflux antenna is unsuitable for frequency reuse due to poor cross polarization isolation and, with its high power requirements, is not suitable for high-data-rate transmissions. Also, due to its wide beamwidth, this type of antenna can spread a signal over a wide ground area, subjecting other receivers in the ground receiving area to unintended transmissions.
Typically, remote sensing satellites are tilted while imaging to increase the imaging range. Also, a "step-andstare" technique is often used to improve imaging resolution. To comply with these requirements, imaging satellites are designed for agility, with a tilt angle range of more than 25 deg. This agility requires antennas capable of radiating signals over a more than 90-deg range, and isoflux antennas cannot support this with adequate gain. But high-gain, narrow-beam antennas can provide a practical solution while reducing requirements for satellite RF and DC power.
Because of its narrow beamwidth, a high-gain antenna must be steered to direct the beam to a desired ground station. This can be accomplished by either mechanical or electrical steering by controlling the phase of the signals fed to the radiating elements of an array antenna. For high-resolution imaging satellites, electrical steering is preferred since mechanical steering may cause jitter due to rotating motors. Phased-array antennas offer a practical solution to systems requiring electrical beam steering.
In a planar phased-array antenna, the beam can usually not be steered more than 60 to 70 deg. from normal without suffering a reduction in antenna gain. The variation is approximately given by (cos θs)α, where θs is the scan angle from normal to the surface and α is a parameter used to account for scan loss. A value of α = 1 corresponds to an ideal case with no mismatch. A value greater than 1.0, to as high as 1.3, accounts for increasing mismatch loss as the beam is scanned away from normal.6 The reduction varies roughly as the projection of the antenna surface in the scan direction (Fig. 4, left).
In principle, several planar arrays, each pointing in different directions, can scan a wide coverage area. In a multisurface array having few large planar surfaces with several radiators per surface, one surface is used at a time. The beam from one planar array is phase steered to a maximum value and at the edge of scan, the adjacent plane surface takes over for wide angular coverage. A more effective approach, however, is a conformal array antenna with radiating elements evenly distributed on a smoothly curved surface. The surface can be made of small planar facets with one or more radiators per facet.
Continue on Page 2
Page Title
To achieve hemispherical coverage, a number of generic surfaces can be used, but the spherical approach allows all radiating elements to be mounted within the same environment, simplifying the design effort and allowing a near-uniform element distribution. The antenna pattern characteristics remain unchanged as the active region is moved over the spherical surface. The effective area of a curved, conformal array is the projection of the active part of the array in the beam direction (Fig. 4, right). The radiation pattern from uniformly excited radiating elements on a hemispherical shell with radius R and phased for maximum radiation in direction ? is the sinc function shown in Eq. A, where a = (4 /?)sin(?/2). If the active region is enlarged, the directivity increases, unless the element spacing becomes too large, leading to increased losses in the grating lobes. To simplify the analysis, it was assumed that the elements had circular polarization with a cosine amplitude pattern. In the analysis for this report, uniform element excitation was assumed and mutual coupling was neglected. Element distribution was made as uniform as possible using a icosahedron distribution approach where elements were evenly distributed on each triangle and then projected onto the surface of a circumscribed hemisphere.
Beam steering was accomplished by shifting the active elements in small steps across the hemispherical array and simultaneously adjusting the element phase to produce a plane wave front with maximum directivity in the required beam direction. The extent of the active area in the curved case is one parameter that must be selected when designing the array antenna. Each element is pointing in a direction normal to the surface. The angle between normal and the desired scan (beam) direction determines whether the element is active. Assuming a maximum useful scan angle of 60 deg., the antenna design's hemispherical surface provides an active area subtended by a conical angle of 120 deg.
The effective area is given by Aeff = (3/4) R2 and can be expected to be independent of the scan direction with a spherical surface. However, since we are dealing with hemisphere, for scan angles larger than a certain value, in our case 30 deg. from the zenith, the effective area decreases and is halved at 90-deg. scan limit. For scan angles, ?, between 30 and 90 deg. from the zenith, the effective area variation is given by Eq. B, where
cos? = cos?,
cot?max,
sinX = sin?max,
sin? and ?max = maximum local scan angle.
Dividing by the total area 2 R2 provides the performance index with respect to the scan angle (solid line in Fig. 5). The gradual reduction in effective area and performance (EIRP) from the 30-deg. scan angle and onward is due to the cutoff of the lower part of the hemisphere (Fig. 5). One alternative is to extend the sphere downward to make the effective area constant with scan. But this increases the total area and the cost of the array. Figure 5 (dashed line) shows the normalized performance versus scan angle from zenith for an extended sphere with constant effective area.
Normally, a suitable radiating element distribution, based on a geodesic or icosahedron configuration, is used in an antenna array to maintain uniform pattern while scanning. The geodesic approach provides uniformly spaced poly faces but accommodates only 20 elements resulting in too low a number. With an icosahedron, each face being an equilateral triangle, all the elements can be accommodated with uniform spacing. This offers desirable spacing for any sphere diameter but, due to the hemispherical surface, a gradual reduction in gain beyond a 30-deg. scan angle (Fig. 5).
Typically, a satellite's onboard antenna travels in an orbit 600 km from earth, and subtends a maximum angle of about 66 deg. with the ground station (Fig. 1). When biases in pitch, roll, and yaw are applied, the resultant subtended angle can change from 40 to 90 deg. As a result, for a groundstation elevation range of 40 to 60 deg., an EIRP of +22 dBW is required for transmissions of about 200 MB/s. For angles of less than 40 deg., the EIRP can be less (Fig. 2).
As an alternative to traditional antennas for remote sensing satellite systems, an active spherical phased array was developed. An increase in the radius of the sphere can increase the directivity if the sidelobe levels are kept low (below -15 dB) and pseudo grating lobes formation is avoided. This can be accomplished by maintaining inter-element spacing within 0.8?. This is done by adding more elements as the sphere is made larger. Via computer-aided-engineering (CAE) simulations, it was found that 96 elements mounted in 8 bands at 0, 12, 24, 36, 48, 60, 72, and 84 deg. with respect to the vertical axis with 1, 3, 6, 10, 16, 20, 20, and 20 elements in corresponding bands on an hemisphere were needed for EIRP of +22 dBW for two simultaneous beams, with 100 mW X-band power fed to each element. Various hemisphere sizes were considered with radiation patterns evaluated for hemispheres of radius 2.5?, 3?, 3.5?, 4?, 4.5?, and 5? (Fig. 6).
The directivity of a 96-element hemispherical array is computed and shown in Fig. 7. As the diameter/radius of the hemisphere was varied, initially the directivity increased linearly to a radius of 3?, reaching a maximum around this value. When the radius was increased beyond this point, the directivity fluctuates. The half-power beamwidth decreases with increasing radius. Theoretically, with a reduction in the half-power beamwidth, the directivity should increase, but this does not happen due to increase of sidelobes or due to generation of significant pseudograting lobes. For a fixed number of elements, the maximum directivity is limited. A hemisphere design with 3.5? radius was found to be best tradeoff with respect to directivity, radiation pattern, and grating/sidelobe levels.
In a spherical array, only those elements that contribute significantly to form a radiation beam in the desired direction need to be excited. An array can be defined by directions of pitch, roll, and yaw, in addition to the desired beam directions. If a cone with cone angle of 2a defines a beam, the maximum value of directivity depends on semicone angle a. Figure 8 shows the simulated radiation patterns of a hemispherical array for different cone angles, while the table offers the results of CAE simulations. From the simulations, excitation of radiating elements in a 60-deg. half cone angle provides optimum performance.
For angles exceeding 60 deg., the number of active elements increases significantly while the directivity does not increase proportionately due to the fact that for a given beam direction from the spherical surface, the contribution from all elements is not the same in that direction (and the +22 dBW EIRP is a driving requirement). With an increase in cone angle, there is no significant improvement in directivity, but a significant increase in wide-angle sidelobes levels. The sidelobe levels should be maintained 15 dB below the main lobe. In a phased array, each element has an amplifier and phase shifter, so that the DC power requirements increase as elements are added. As power dissipation increases, the array temperature increases without necessarily increasing the EIRP.
For the spherical antenna array design, a semicone angle of 60 to 75 deg. was chosen with a set of elements selected for beam steering to an extent of 12 deg. in both elevation and azimuth planes by varying the phase of the elements. Directivity is a function of the subset of elements made active. As the beam direction changes by more than 12 deg. in one plane, a different set of elements is activated. The changeover occurs at the footprint of the cone on the spherical surface. As the beam is scanned, the footprint of the cone moves in the direction of the beam, with some elements activated and some deactivated.
Figure 9 shows the fabricated active spherical phased array with 96 radiating elements as flown on an Indian remote sensing satellite. It transmits X-band QPSK modulated carriers through two independently steerable beams to two ground stations simultaneously. Its radiation patterns were measured in an anechoic chamber, with Fig. 10, left, showing patterns for two beams in different directions and Fig.10, right, showing patterns for a single beam. Measured data agree with CAE simulation results.
ACKNOWLEDGMENT
The authors would like to express their sincere gratitude to Mr. P.K.Reddy, Mr. V.V. Srinivasan, Mr. Parimal Kumar, Ms. N. Ramalakshmi, Dr. V.K. Lakshmeesha, and other colleagues at the Communication Systems Group of the ISRO Satellite Centre for their contributions in simulating and fabricating the phased array. The authors would also like to express sincere thanks to the Director of the ISRO Satellite Centre for the encouragement given in developing the X-band phased-array system.
REFERENCES
1. V. Sambasiva Rao and Surendra Pal, "Techniques for High Bit Rate Data Transmission from Remote Sensing Satellites," IEEE International Symposium on Microwaves, Bangalore, India, Dec. 15-17, 2006.
2. V. Sambasiva Rao and Surendra Pal, "A Unique Space to Earth Data Transmitting System. International Astronautical Congress - IAC 2007, Hyderabad, India, Sept. 24-28, 2007. 3. V. Sambasiva Rao, "X-band high bit rate QPSK Modulator," IETE Technical Review, Vol. 1, No. 4, July-August 1993, pp. 305-309.
4. V. K. Lakshmeesha, L. Nicholas, V. Mahadevan, and S. Pal, "S-band shaped beam antenna for Indian Remote Sensing Satellite," IEEE AP symposium, Vancouver, Canada, June 1985, pp. 629-632.
5. A. Kumar, "Highly shaped beam telemetry antenna for the ERS-1 satellite," Proceedings of IEEE, Montech;1986; Conference on Antennas and Communication. Montreal, Canada; 1986, October, IEEE Catalog No. 0156-0.
6. Lars Josefsson and Patrik Persson, Conformal Array Antenna Theory and Design, IEEE Press Series, Wiley-Interscience, New York, 2006