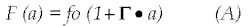Acceleration force can alter the performance of a quartz crystal or crystal oscillator. The nature of the effect depends on the type of force that is being applied. Changes in the static gravitational force such as tilting or rotation will cause a step offset in frequency. Time-dependent acceleration or vibration will create frequency modulation in an oscillator. This will generate discrete sidebands in the case of sinusoidal vibration or an increase in the noise floor with random vibration. A shock pulse will cause a sharp temporary perturbation in the output frequency. What follows is an examination of the effects of acceleration force on the performance of quartz crystals and crystal oscillators.
The magnitude of these frequency shifts is a function of the quartz crystal's acceleration or "g-sensitivity" vector and the magnitude and direction of the applied acceleration force. The acceleration sensitivity of quartz crystals is caused by stresses resulting from the mass of the resonator blank reacting against its mounting structure.1 This sensitivity is determined by many factors such as the type of cut—such as stress compensated (SC) or AT, the design and processing of the quartz blank, the package type, mounting structure and orientation in the holder. The range of typical g-sensitivities for bulk-mode quartz crystals can span several orders of magnitude, from less than 1 × 10-10 per g for a carefully made precision SC crystal to greater than 1 × 10-7 per g for a low cost AT crystal.2
Since their magnitudes are relatively small, these effects go undetected in many applications with standard oscillators such as voltage-controlled crystal oscillators (VCXOs). With precision oven-controlled crystal oscillators (OCXOs) or sources designed for severe environmental conditions, the inherent acceleration sensitivity can be very significant. If the oscillator is deployed in a high-vibration environment such as an airborne platform, increased phase noise or discrete spurious components will appear as modulation on the output signal, degrading the performance more than all other sources of noise combined. Even in a benign environment, an OCXO may experience significant frequency shifts due to static g-forces by moving, tilting, or rotating motions.
A crystal oscillator's g-sensitivity is usually characterized by measuring the attributes along three mutually perpendicular axes parallel to the faces of the oscillator package. However, the intrinsic acceleration characteristic of quartz consists of a single vector at some angle that is usually not normal to any of the faces of the package (Fig. 1). Therefore, the resonant frequency during acceleration is a function of the product of the two vectors:
where:
fo = the center frequency of the resonator with no acceleration,
F(a) = the resonant frequency of the crystal with acceleration,
a = the applied acceleration, and
Γ = the acceleration sensitivity vector of the crystal.3
By measuring the individual mutually orthogonal components in the x, y, and z axes, the magnitude and orientation of the g-sensitivity vector, Γmax, can be determined. Using the following trigonometric identities, Γmax can be calculated without any prior knowledge of the crystal itself:
Once the magnitude and angular orientation of Γmax are known, the expected effect of externally applied acceleration forces in any direction can be determined. When the direction of the applied force is parallel to the axis of Γmax, it will have the greatest influence on the crystal frequency. As the angle of the applied force moves away from the axis parallel to Γmax, the resultant effect rolls off as the cosine of the angle α, which is defined as the difference between the direction of applied force and Γmax. For any direction of applied acceleration, the frequency shift is given as the product of the g-sensitivity vector, Γmax times the applied force (α):
Since the frequency deviation rolls off as the cosine of the angle α between α and Γmax, a circle is defined as shown in Fig. 2.4 If viewed in all three dimensions, this would appear as a sphere with Γmax along its axis. Therefore, the resultant g-sensitivity of the crystal in any direction as a function of Θ and Φ can be given by:
When the force is applied in the opposite direction, a frequency shift of equal magnitude but opposite sign is produced, defining the second circle in Fig. 2. Because of the vector and cosine nature of the g-sensitivity vector, an interesting attribute of this characteristic is that a plane of zero g-sensitivity is present. This is defined by the plane that is normal to Γmax. This shows that any force applied to the crystal that is perpendicular to Γmax will have no effect on the frequency. If the operating environment of the oscillator is such that the most severe acceleration or vibration forces are applied in one known direction, it is possible to orient the oscillator so that frequency shifts will be minimized.
Because of the relatively small frequency shifts that must be measured when characterizing a crystal oscillator's g-sensitivity, specialized test setups and high-resolution instruments are required. One of the most straightforward ways of making basic measurements on a precision oscillator is to use changes in the Earth's gravitational field to cause shifts in the oscillator frequency. This technique is known as the "2-g Tipover" method. The oscillator is placed in a fixture or on a bench and the frequency is monitored until it is stable. The unit is then flipped upside down or rotated 180 deg. and the frequency is once again measured. A unit initially experiencing a gravitational force of 1 g in the downward direction will be subject to a force of 1 g in the opposite direction after beng flipped. The net effect is a change of 2 g. Therefore, the amount of frequency shift measured divided by 2 is the oscillator's g-sensitivity in that axis. The procedure is then repeated for the other two axes. Although conceptually simple, the method requires an extremely stable oscillator to consistently measure the small frequency shifts that occur. Thermally induced short-term drift and modulation due to the connecting cables typically render this method invalid for uncompensated oscillators, although it is used with OCXOs and tightly compensated TCXOs (Fig. 3).
Page Title
In order to obtain a precision dynamic measurement, the performance of the crystal is measured while vibration is applied. When a crystal is subjected to sinusoidal vibration, the output of the oscillator will be frequency modulated with sidebands at the vibration frequency. The level of the sidebands may be determined with Eq. 7 using the standard frequency-modulation (FM) index formula (as long as the modulation index is relatively small).
Given that fm equals the vibration frequency fv and G is the peak applied vibration level, Δf is given by
which may be rewritten as Eq. 9.
Using a high-dynamic-range, narrowband spectrum analyzer, it may be possible to measure these sidebands directly. If necessary, the modulation index and consequently the sideband levels may be increased by multiplying the frequency of the crystal. This will result in an increase of sideband level of 20logN where N is the multiplication factor. Measurement resolution can be improved by phase locking another oscillator to the device under test (DUT) to suppress the carrier signal. Figure 4 shows a standard test setup for measuring vibration-induced effects, using a very sensitive low-noise phase-locked-loop (PLL) frequency discriminator.
To measure the vibrational characteristics of a resonator, the device to be tested is mounted on the vibration table in the proper orientation. The oscillator and crystal must be rigidly attached to the vibration fixture to avoid any mechanical resonance in the frequency range to be measured. The power leads and output cable must be held firmly in place with tape or glue to minimize the effect of vibration due to cable movement. In order to achieve the most accurate measurement of the g-sensitivity of just the crystal, it is necessary to remove the oscillator sustaining circuit from the vibration table so that only the crystal is exposed to the vibration. The connections are then made to the crystal through impedance-matched cables.5 Apparent effects of including the sustaining stage on the vibrated assembly may be higher than 1 × 10-10/g. To downconvert the oscillator's frequency to baseband, the DUT is phase locked to a second reference oscillator at the same frequency. The baseband modulation present on the oscillator output as a result of the vibration is then measured with a low-frequency spectrum analyzer. This portion of the test set is typically a commercial phase-noise measurement system.
While sinusoidal vibration generates discrete sidebands at the vibration frequency, the effects of random vibration are more complex, causing a general rise in the noise floor. By knowing the power spectral density (PSD) of the vibration input, it is possible to compute the g-sensitivity of the crystal from the resultant phase noise plot. The sideband formula given above is modified to use the PSD of the vibration input giving Eq. 10.
Figure 5 shows the phase noise of a 100-MHz OCXO at rest and also with random vibration applied. Even moderate levels of random vibration can degrade the phase-noise performance of an oscillator by 40 or 50 dB. Mechanical resonances related to the crystal's mounting structure are often excited in the 1-to-4-kHz region and must be accounted for in critical applications
In some systems, the most prevalent type of acceleration is a short-duration shock pulse. These types of disturbances that can occur from handling and movement of equipment are often characterized as "microphonics." This type of event produces a momentary perturbation in the frequency of the oscillator as the resonant frequency of the crystal follows the applied force. After the shock pulse, the resonator should return to the original frequency unless the pulse was severe enough to cause damage to the mounting structure or circuit. If the oscillator is a reference in a narrowband PLL, this type of disturbance could cause the loop to break lock. This type of momentary excursion of the frequency is difficult to measure directly, but can be captured with a test setup using a digital storage oscilloscope (DSO). To measure this, the oscillator under test is mounted on a shock table. The unit is then phase locked to a reference oscillator or synthesizer. The error voltage is fed back through a loop amplifier and a wide bandwidth loop filter so that the loop will track the shock pulse even with a fast rise time. As a shock pulse is now applied to the unit under test, the frequency of the oscillator will shift in accordance with the magnitude of the shock pulse and the size and relative direction of the crystal's g-sensitivity vector. The g-sensitivity of the crystal in the direction of the applied pulse may be found by measuring the amplitude of the pulse developed on the automatic-frequency-control (AFC) loop voltage as recorded on the oscilloscope. The g-sensitivity (Γ) is determined according to
where:
A = the voltage pulse amplitude,
S = oscillator tuning sensitivity, and
SP = the level of the shock pulse.
Conversely, if the acceleration sensitivity of the crystal and the expected g-level of the shock pulse are known, the amount of frequency shift that will be experienced can be calculated.
Actual measurements of groups of crystals show that even with careful design and attention to details such as consistency of orientation and mounting, a large spread in the magnitude of the g-sensitivity vector as well as its direction is still present. When examining data (not shown) on the magnitude of the g-sensitivity vector for a group of 100-MHz fifth-overtone SC-cut crystals in TO-5 holders all supposedly manufactured under identical conditions, significant differences were still evident within the group.
Applications requiring the lowest acceleration sensitivity usually call for SC-cut crystals. The SC-cut crystal reveals an average Γ that is two to four times better than a similar AT-cut crystal at the same frequency. The AT-cut crystal, however, typically shows less variation in the distribution of both the magnitude and direction of Γ.5
The direction of the applied acceleration force relative to the orientation of the g-sensitivity vector will have a large effect on the resulting frequency shift. If it is known that the most severe vibration or acceleration forces will be experienced primarily in one direction, it may be possible to orient the mounting of the oscillator to minimize the effects. After measuring the apparent Γ in each axis, the unit should be mounted if possible with the axis that has the lowest g-sensitivity parallel to the direction of the worst-case vibration. If the oscillator mounting structure can be rotated, the Γ vector may be pointed perpendicular to the applied vibration putting the assembly in the plane of "zero g-sensitivity." In real-world applications, all of the vibration and applied acceleration does not come from a single direction, so zero g-sensitivity will not be achieved, but improvements may be realized with the proper orientation.
Page Title
Another method of reducing the detrimental effects of environmental forces is through the use of vibration and shock isolators to isolate the crystal and the sensitive portions of the oscillator circuit. To be most effective, the isolation system must be carefully designed, taking into account such factors as the frequency range and levels of the applied vibration, the weight of the isolated assembly and the spring factor characteristics of the isolators. The dynamic response curves of the transmissibility show that the isolation is only effective above the resonant frequency (fn) of the system, which may typically be around 100 Hz. Below the resonant frequency, the vibration is still passed to the crystal, and depending on the quality factor (Q) of the system, may exhibit significant amplification or peaking just below fn (Fig. 6). An isolated oscillator may need to undergo a sinusoidal resonant dwell vibration test, which can place great stress on the isolators. This could even lead to significant self-heating and eventual failure of the system.6 Another concern is that the isolators be isoelastic so that the translational spring rates in all axes are the same, providing multiple-axis isolation with similar characteristics. Care must be taken in properly designing and specifying an isolation system, but this will usually provide considerable benefit in a harsh environment.
Another method to achieve g-sensitivity improvements involves applying active feedback from an accelerometer to compensate for or cancel the effects of vibration on the crystal. Several configurations have been reported which have achieved some significant improvements.3,7 This technique consists of sensing the applied acceleration with an accelerometer and then amplifying and phase-inverting the sensing signal before applying it to an FM port on the oscillator. Specifications of the available accelerometers have improved over recent years making this approach more practical to implement. For complete cancellation, a three-axis accelerometer should be used with the sensitivity calibrated in each axis. Alternatively, a single axis accelerometer can achieve cancellation in all directions if certain conditions are met. The accelerometer must have a sensitivity that rolls off as cosΘ when the direction of applied force moves away from its most sensitive axis. This matches the directional sensitivity of the crystal relative to Gmax. The accelerometer must then be oriented such that its sensitive axis is pointing in exactly the same direction as the crystal's g-sensitivity vector.
To suppress vibration effects, it is necessary to accurately match the amplitude of the accelerometer signal to the sensitivity of the tuning port of the oscillator as well as the phase of the signal to the induced frequency shift of the crystal. The direction of the frequency shift must also be matched to the compensation signal. Without prior knowledge of the crystal vector direction, it is necessary to provide for inversion of the signal depending on the relative direction of the vector to the sensitive axis of the accelerometer. For suppression on the order of 40 dB, the amplitude must be matched to better than 1 percent and the phase to 0.5 deg. The compensation circuitry must be carefully designed and calibrated and must employ low-noise devices to ensure that the phase noise of the oscillator is not degraded.
A passive method of canceling the effects of acceleration is possible by using a second crystal with a similar acceleration sensitivity vector.8,9 Cancellation of the g-sensitivity can be achieved by orienting the second crystal such that its g-sensitivity vector is antiparallel to the first and then operating them in series in the same oscillator circuit. The crystals must be measured and oriented very accurately, requiring some form of two-axis gimbal mount for one of the crystals so that it can be rotated in three dimensions to line up with the crystal vector. Matching the direction of the two vectors to within less than 1 deg. can be difficult.
Many manufacturers of quartz crystals have attempted to reduce the acceleration sensitivity of the resonator itself. A perfectly symmetrical mounting structure relative to the active region of vibration on the quartz blank is critical. Other characteristics of the holder and mounting structure can also be significant.10,11 Some special stress-free mounting arrangements have been proposed to achieve this goal.12 Theoretically, if the crystal is completely symmetric with respect to the mode shape, the acceleration sensitivity can be zero. But even very small deviations from this ideal condition will cause significant degradation. The capabilities of the best commercial resonators, however, has not changed much in the past 20 years, with the best acceptable specification still being about 2 × 10-10 per g for screened SC-cut crystals.
REFERENCES
- M.H. Watts, E.P. EerNisse, R.W. Ward, and R.B. Wiggins, "Technique for Measuring the Acceleration Sensitivity of SC-Cut Quartz Resonators," Proceedings of the 42nd Annual Frequency Control Symposium, 1988, pp. 442-446.
- J.R. Vig, "Quartz Crystal Resonators and Oscillators—A Tutorial," June 1999.
- R.L. Filler, "The Acceleration Sensitivity of Quartz Crystal Oscillators: A Review," IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 35, No. 3, May 1988, pp. 297-305.
- J.M Przyjemski, "Improvement in System Performance Using a Crystal Oscillator Compensated for Acceleration Sensitivity," Proceedings of the 32nd Annual Frequency Control Symposium, 1978, pp. 426-431.
- M.M. Driscoll, "Quartz Crystal Resonator G Sensitivity Measurement Methods and Recent Results," IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,Vol. 37, No. 5, September 1990, pp. 386-393.
- D.S. Steinberg, Vibration Analysis for Electronic Equipment, Wiley-Interscience, New York, 1988, pp. 302-308.
- V.J. Rosati, "Suppression of Vibration-Induced Phase Noise in Crystal Oscillators: An Update," Proceedings of the 41st Annual Frequency Control Symposium, 1987, pp. 409-412.
- R.L. Filler, "Acceleration Resistant Crystal Resonator," United States Patent No. 4, 410, 822 (1983).
- F.L. Walls and J.R. Vig, "Acceleration Insensitive Oscillator," United States Patent No. 4,575,690 (1986).
- R.J. Besson, J.J. Boy, and F. Deyzac, "Acceleration Sensitivity of BVA Resonators," Proceedings of the 1996 Annual IEEE Frequency Control Symposium, pp. 457-463.
- W.P. Hanson, T.R. Meeker, and L.C. Heishman, "A New Factor Affecting the Acceleration Sensitivity of the Resonance Frequency of Quartz Crystal Resonators," Proceedings of the 44th Annual Symposium on Frequency Control, 1990, pp. 478-487.
- R.B. Haskell, P.E. Morley, and D.S. Stevens, "High Q Precision SC-Cut Resonators with Low Acceleration Sensitivity," Proceedings of the 2002 IEEE Frequency Control Symposium, pp. 111-118.