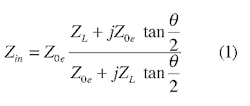Low-temperature-cofired-ceramic (LTCC) technology offers the means to integrate active and passive components on compact modules for both commercial and military applications. This elegant technology can provide tremendous benefits in terms of high performance and small size, but requires careful design discipline to achieve repeatable results. Fortunately, a novel procedure using Ansoft Designer from Ansoft (Pittsburgh, PA) allows passive and active modules such as power amplifiers (PAs), RF switches, and RF front-ends to be designed quickly and easily on LTCC substrates.
An LTCC process can integrate capacitors, resistors, and inductors in a very small area, while allowing active devices such as RF integrated circuits (RF ICs), monolithic microwave integrated circuits (MMICs), and surface-mount devices to be mounted on them. Once completed, the process produces a mechanically strong, hermetically sealed, thermally conductive, chemically inert, and dimensionally stable structure with high yield. However, designers face significant challenges when designing components with the LTCC process. Fortunately, the use of the latest design tools such Ansoft Designer can overcome these challenges, while providing a high level of confidence in the viability of the result.
Many challenges face designers working with LTCC, including the need for RF characterization of internal structures that lack electrical models. Most embedded components, especially spiral inductors and parallel plate capacitors, are large in area. Parasitic coupling from such large structures with other structures or to ground planes is often significant. The process for characterizing passive devices must include parasitic effects, not only to determine passive component values, but also to evaluate any unintentional or intentional coupling to other structures. Reliable RF characterization of these coupling mechanisms must be developed to ensure design success. It is also important to generate a component library so that often-used components can be readily incorporated into future designs.
Ansoft Designer combines the company's High Frequency Structure Simulator (HFSS) simulation tool for characterizing three-dimensional (3D) structures with system, circuit, and planar EM simulation. The combination makes the tool well suited for LTCC design and development because it includes the rigorous EM simulation required for RF characterization.
Various technologies are required to design integrated LTCC modules. EM-based simulation is used for characterization of passive elements and circuit simulation is used for RF module design and optimization. Model library development is accomplished using an integrated equivalent-circuit extraction capability. In addition, the system simulation integrated within Ansoft Designer allows users to fully characterize the design at the system level.
Planar EM is a 3D planar field solver based upon method-of-moments (MoM) techniques. With its singular-value-decomposition (SVD) FastSolve technology, Planar EM can simulate very complex structures, allowing designers to characterize the complexities found in LTCC modules. HFSS can be used to examine structures that are not strictly planar, and can perform packaging analysis, making it possible to characterize the effects of module interconnection to a higher-level assembly.
The procedure for building embedded passive models and an embedded passive model library is the same for LTCC modules and for printed-circuit boards (PCBs). The procedure begins with physical model analysis using some form of EM simulation. HFSS, Planar EM, or Spicelink 3D can be used to extract electrical performance. HFSS is a full-wave 3D solver and should be used for high frequencies and complex geometries. Often the embedded passive devices are predominantly planar in nature with minimal coupling to other 3D elements. In this case, the built-in Designer Planar EM is the best choice. Spicelink 3D is similar to HFSS; however, it is based upon a static field solution. It typically completes simulation faster than HFSS and should be used whenever the structure is small compared to wavelength.
The next step in model development is to select an equivalent-circuit model. Often a simple pi or T network is sufficient for small two-terminal devices. Optimization engines within Ansoft Designer automatically adjust equivalent-circuit parameters until circuit performance matches the EM simulation extracted electrical performance.
An embedded capacitor geometry and its associated equivalent circuit are shown in Fig. 1(a). The geometry is a simple parallel-plate structure. The equivalent circuit includes parasitic resistance and inductance as well as fringing capacitances. Parallel capacitance value and parallel parasitic parameter values can be found by fitting the S-parameters between the equivalent-circuit model and performing HFSS 3D simulation within the proper frequency range. The Q value can be calculated from a terminated one-port Z11 parameter using Q = mag11)/real(Z11)>. The self-resonance frequency (Fr) should be investigated for any capacitor because the reactance value of may not be capacitive at frequencies above the resonance frequency.
Figure 1(b) shows the variation of capacitance value of the embedded capacitor in terms of the overlapped area between parallel plates, along with the parasitic inductance and resistance values. Ansoft Designer can use this graph to obtain the required capacitance value by embedded parallel plates, and results from the analysis can be used to construct a capacitor library for frequently used values.
Similarly, Fig. 2(a) shows the geometry for an embedded inductor based on a simple, single-layer spiral structure along with its equivalent circuit. The equivalent circuit includes parasitic series resistance and a shunt capacitance. As with the embedded capacitor, the S-parameters found from a 3D HFSS simulation are used in an optimization to find the inductance and the parasitic resistance and capacitance across a desired frequency range. The inductor Q can be calculated from terminated one-port Z11 parameter using Q = mag11)/real(Z11)>. An inductor also has a self-resonance that should be investigated so that the inductor is used below this frequency.
Inductance versus the number of turns of the embedded spiral inductor is extracted in the analysis and shown in Fig. 2(b). Ansoft Designer can use this data to obtain required inductance values for embedded inductors. This data, coupled with the parasitic capacitance and resistance values, can be used to construct an inductor library for frequently used values.
Page Title
Embedded resistors have significant advantages compared with their chip-resistor counterparts. They are very small, which allows them to be fully integrated within the LTCC module, and have broad applicability since resistance values can be varied from 1 Ω to 1 MΩ. Nevertheless, embedded resistors provide some challenges, such as resistor tolerance and sheet resistivity.
An embedded resistor geometry is a rectangular structure with finite length, width, and height, the equivalent circuit includes parasitic capacitance and inductance. By fitting the S-parameters between the equivalent-circuit model and an HFSS 3D simulation within the proper frequency range, the parallel capacitance value and series inductor parameter values can be found.
The resistance variation of the embedded resistor in terms of the aspect ratio of the film resistor is extracted in the analysis. Since different types of film have independent surface resistance values, the range of resistance that can be obtained varies with the material. A library of resistors can be developed using this information.
Geometric parameterization of planar EM or 3D structures in Ansoft Designer and HFSS, respectively, allow users to develop LTCC design kits based on various embedded LTCC components. Ansoft Designer's Solver On Demand technology permits circuit designers to implement initial LTCC designs using equivalent-circuit models for rapid prototyping followed by more rigorous EM design verification using the synchronized layout information. Circuit/planar EM co-simulation can be performed for individual LTCC components or the entire LTCC design (Fig. 3).
LTCC technology allows lumped elements to be implemented conveniently in a compact size. In this example, a 10-dB directional coupler was designed using LTCC lumped elements rather than coupled lines. The design procedure is based on the classic coupled-line directional coupler, with modifications to allow lumped rather than distributed elements. The derivation provided below shows how to compute lumped element values that provide equivalent coupling to traditional coupled lines. Directional coupler performance of the lumped element equivalent circuit is evaluated using Ansoft Designer's linear analysis. Embedded passive devices with appropriate lumped element values are designed using EM simulation, and comparisons can be made between the circuit simulation and a full 3D geometric implementation and EM simulation.
Figure 4 shows a pair of coupled lines with an electrical length of θ = 2πl/λ as well as their equivalent circuit. Maximum coupling occurs when l = λ/4, so coupled-line directional couplers are typically set to this length. A direct equivalent circuit for the structure would include capacitances to ground as well as capacitive coupling between coupled lines. Self-inductance and mutual inductance is used to model the distributed nature of the line as well as the magnetic coupling between lines, respectively. Although it is possible to create a lumped-element implementation with self and mutual inductances, both design and manufacturing would be a fairly difficult. Design of an isolated inductor is fairly straightforward, while designing a pair of inductors with specified self-impedance and mutual impedance is far more complicated. In addition, the mutual impedance requirement might create a sensitive design that would be difficult to manufacture. For these reasons, it is desirable to find an alternative equivalent circuit that has no mutual terms.
Figure 4 shows that the alternative equivalent circuit does not require a mutual inductance term. This circuit is a modified pi network with the distributed inductance divided into two equal-valued inductors (Le) and a coupling inductor (Lc) to represent the mutual effect. The challenge is to determine the values of the various capacitors and inductors so that the ideal lumped-element circuit is equivalent to the coupled lines.
In the equivalent circuit, the two symmetry planes that can be configured as electric or magnetic walls (boundary conditions). Taking the various combinations of electric or magnetic walls will result in four possible combinations that can be used to solve for the four passive component values Ce, Le, Co, and Lo.
Page Title
Placing a magnetic wall along the longitudinal symmetry plane results in the even mode on the coupled lines. In the equivalent circuit, the longitudinal magnetic wall results in an open circuit for any conductors that cross the symmetry plane. Toggling the transverse boundary condition to either a magnetic boundary or an electric boundary results in an open circuit or a short circuit, respectively, for conductors traversing the boundary. In each case, the characteristic impedance of the portion of the coupled transmission line is the even impedance Zoe and the electrical length is one-half of the original electrical length. The input impedance looking into the transmission line is given by:
For the transverse magnetic wall case, there is an open circuit at the end of the line where ZL = (infinity) and Eq. 1 becomes:
The input impedance looking into the equivalent circuit is simply the impedance of the capacitor Ce given by:
Equating Eqs. 2 and 3 makes it possible to solve for Ce:
For the case of an electric wall in the transverse direction, input impedance looking into the transmission line is given by Eq. 1. This time, however, there is a short circuit at the end of the transmission line, so ZL = 0 and Eq. 1 becomes:
It is easier to utilize the admittance when equating to the equivalent circuit because the equivalent circuit is the parallel combination of an inductor and a capacitor. The corresponding input admittance is:
The input admittance looking into the equivalent circuit is given by:
Equating Eqs. 6 and 7 with the use of Eq. 4 helps solve for Le:
This same procedure can be used to derive the odd-mode impedance Zoo using a longitudinal electric wall. The odd mode inductance and capacitance are given by:
and
The final step for designing a lumped-element directional coupler is to provide a method for determining the required Zoe and Zoo to plug in to the equations for the even and odd inductances and capacitances. These parameters are determined from the desired coupling value.1:
Parameter Zo can be chosen based on design requirements. Coupling coefficient Cdb for this design is 10 dB. Equations 11, 12, and 13, along with Eqs. 4, 8, 9, and 10, form the basis for the design. Choosing a center frequency of 2 GHz and an electrical length of λ/4 results in the these values for the passive elements: Ce = 2.21 pF; Le = 1.43 nH; Co/2 = 0.53 pF; and Lo = 1.55 nH.
The circuit was entered into the software and a frequency sweep from 1.5 to 2.5 GHz was simulated. The frequency resulted in a center frequency of 2 GHz and a coupling value of 10 dB.
Now the lumped elements can be incorporated in an LTCC substrate. Capacitors can be implemented with a simple parallel plate structure, and inductors can be implemented using a helical structure with vias traversing from layer to layer. Simulations helped to optimize the lumped element values (Fig. 5).
The results of the directional coupler modeled in HFSS (Fig. 6a) compared to the results of the ideal circuit simulation (Fig. 6b) clearly show that 10-dB coupling was achieved, and that the derivation of the equivalent circuit model is a viable approach to LTCC design.
REFERENCE
- S.B. Cohn, "Shielded coupled-strip transmission lines," IRE Trans., PGMTT-3, Oct. 1955, pp. 29-38.