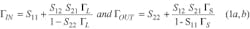Amplifier performance can be enhanced by understanding the electrical requirements of the active device, the transistor. As was seen last month in the second part of this article series, adding the appropriate stabilizing circuitry can make a transistor unconditionally stable so that it does not oscillate at any frequency regardless of source and load impedances. This third part of the article series will show how to tune the input and output of the transistor to obtain higher gain using the unilateral gain design method.
It has been shown that S-parameters are a valuable aid both for collecting data for a transistor and then using the data to predict performance and design an amplifier circuit. As noted in Part 1, unlike Z, Y, or ABCD parameters, the values of S-parameters depend not only upon the properties of the transistor but also upon the source and load circuits used to measure them. This is because they measure transmitted and reflected waves, and these depend upon both the transistor and the source and load used to test it (Fig. 1).
The concepts of a reflection coefficient and traveling waves can be used even if there are no actual transmission lines at the device ports. One might expect that the input reflection coefficient, ΓIN, would simply be equal to S11, and that ΓOUT would be equal to S22. However, because of feedback these must be corrected:
The general transducer gain of a two-port network having S21 and S12 values, whether it is a transistor or not, is
If S12 = 0, then ΓIN = S11 and ΓOUT = S22. Furthermore, if S12 = 0, the transducer gain becomes:
This can be considered as three separate gain factors:
The unilateral gain (Fig. 2) expressions of Eq. 3 apply for any ΓS and ΓL. To maximize GS, the value of ΓS is first selected as:
Then
Similarly, to maximize GL, the value of ΓL is selected as
and then
Since under the unilateral assumption, S12 = 0, the maximum gain to be obtained from a transistor is:
The overall gain (in dB) to be obtained is then (Fig. 3)
in which it should be recognized that GS and GL are the gains (or losses) to be obtained by matching (or deliberately further mismatching) the input and output circuits, respectively. Of course, there is an error in the gain calculations of Eqs. 8 and 9 if in the actual transistor S12 ≠ 0. In that case, the true gain, GT, is related to the calculated unilateral gain GTU by:
where:
The value of U varies with frequency because of its dependence on the S-parameters and it is called the unilateral figure of merit. For the 2N6679A transistor, applying the S-parameter values at 1 GHz from Table 10.1-1, U is calculated as:
From this it can be seen that the unilateral gain approximation can be used for the 2N6679A at 1 GHz with an error no greater than 1.4 dB. To obtain the "maximum gain" using the unilateral gain design, the 50-Ω source is transformed to ZS = ZIN*, and the 50-Ω load is transformed to ZL = ZOUT*. From the S-parameters,
To unnormalize,
Since the S-parameters have been modified by adding the stabilizing components, revised S-parameters must be used for the stabilized 2N6679A transistor circuit. This would be a laborious task, but is easy and straightforward using network simulator software. The revised S-parameters are shown in Table 1.
There are numerous methods by which the amplifier can be matched. As an example, the Q matching method can be employed.2 To transform a resistance RH to a lower value RL, place a reactance in parallel with it having magnitude RH/Q. Converting to the series equivalent circuit results in a series resistance RL = RH/(1 + Q2). Then resonate the equivalent series reactance with a reactance of the opposite sign. Since the input impedance at 1 GHz is
it is necessary to transform the 50-Ω source to ZIN*. Thus,
The process begins by transforming the 50-Ω source to 10.43 Ω:
Since the transformation from 50 Ω is to a lower resistance (Fig. 4), the conversion begins with a shunt reactance in parallel with the 50 Ω. Since the final transformed value for ZS has an inductive part, a shunt inductor is selected rather than a capacitor. For a Q of 1.948, the reactance of L1 is +25.667 Ω. This can be provided using an L1 given by:
The series equivalent circuit on the right has the required 10.43-Ω real part, and, because the circuit Q is unchanged, a +j20.32-ohm reactive part. However, a +7.238-Ω reactance is required, so part of this reactance must be tuned out using a series capacitor C2. The reactance magnitude of C2 is 20.32 7.24 = 13.08 Ω. This is provided by a capacitor, C2 with the value
The resulting circuit and performance are shown in Fig. 5.
With input tuning, the gain, S21, is about 18.4 dB at 1 GHz, compared with about 15.9 dB for the stabilized (but untuned) transistor alone (from Part 2), a gain improvement of 2.5 dB. This is consistent with the result to be expected in tuning the 2.5 dB mismatch loss of the stabilized transistor, having an S11 magnitude of 0.661 (Table 1). Keep in mind that this S21 is the gain of the overall two-port network in Fig. 5.
Also from Table 1, |S22| = 0.414. This means that 17 percent of the power is being lost due to the output mismatch. If this were recovered, the gain could increase by another 0.8 dB. To tune the output port, the output impedance at 1 GHz is seen from Table 2 to be (88.493 j46.646) Ω. The 50-Ω load is to be transformed to the complex conjugate of this value or
Page Title
Q Matching Method
Using the Q matching method, and starting at the load, the 50 Ω is first transformed to 88.493 Ω, a shift from a lower to a higher resistance. Therefore, the process is started with a series circuit for which, arbitrarily, a series inductor, L2, is chosen (Fig. 6). The resistive transformation ratio is 88.493/50 and the required Q is 0.877, hence L2 is 6.99 nH. The parallel equivalent circuit consists of the desired 88.493-Ω resistance shunted by a parallel inductive reactance of 88.493/0.877 = 100.86 Ω. This is parallel resonated at 1 GHz by a capacitance, C2, of 1.576 pF. An additional reactive impedance of +j46.646 Ω is required to transform the 50-Ω load to the ZL given in Eq. 22, and this is achieved with a series inductor, L3, of 7.43 nH. The stabilized 2N6977A amplifier with unilaterally tuned input and output is shown in Fig. 5 along with its performance.
The gain when both input and output are matched is 20 dB at 1 GHz. This is within 1 dB of the 19.2 dB maximum gain expected. Recall that the unilateral figure of merit analysis indicated that the error in gain estimate could be between 1.18 dB and +1.37 dB. The 20-dB gain is an increase over the input-matched case (Fig. 4) of 1.6 dB. This is more than the 0.8 dB expected improvement. Also, both the input and output are imperfectly matched as can be seen from the plots of S11 and S22 in Fig. 5. These inaccuracies are to be expected in the unilateral gain method, when the transistor's internal feedback, S12, is ignored.
For optimum performance, it is possible to find a source and load impedance pair that perfectly matches the transistor at any given frequency. This approach--the simultaneous conjugate match--will be covered next month in Part 4 of this continuing article series.
REFERENCES
1. Guillermo Gonzalez, Microwave Transistor Amplifiers, Analysis and Design, 2nd ed., Prentice-Hall, Upper Saddle River, NJ, 1984.
2. Joseph F. White, High Frequency Techniques, An Introduction to RF and Microwave Engineering, John Wiley and Sons, Inc., Hoboken, NJ, 2004.