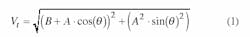Understanding Mismatch Effects In Power Combining Circuits
Power combining theoretically increases an amplifier's effective output power by coherently summing N identical output stages. For example, if one output stage produces 1 W power, coherently combining four stages will effectively increase the output power to 4 W. Practically, the output power will be degraded by the combiner loss and the practical amplitude and phase errors introduced. As the number, N, of channels increases, the difficulty in maintaining minimally acceptable phase and amplitude errors while minimizing the summing device losses grows substantially. In this article, power-combining techniques will be analyzed for two devices, but these approaches can easily be extrapolated to higher-order combining systems.
Image phase mixing is a technique of frequency converting an upper or lower sideband to an intermediate frequency (IF). This manipulation is accomplished by splitting an RF signal into two channels and mixing each of the channels with a local-oscillator (LO) signal. The two IF signals are combined in an unterminated quadrature coupler, with one output yielding the upper sideband and other output producing the lower sideband.
Power combining and image-rejection techniques using an image phase mixer are the respective vector addition and subtraction of two signals. Doubling the output power capability of an amplifier is typically accomplished by dividing the signal into two paths, amplifying the signal with two identical power amplifiers and summing the resulting signals together. The gain is not affected but the output power, i.e., the 1-dB compression point and respective third-order intercept point, is increased by 3 dB.
In real systems, dividers, amplifiers, and combiners are not ideal and have respective gain (amplitude) and phase errors. The effects of the gain and phase errors are readily understood if the signals are represented as phasors (for example, Asinθ , where A is the magnitude in V and is the phase in deg.). The input is a voltage vector divided into two paths, amplified and recombined. Any error in the components shows up as changes in the magnitude and phase. Ideally, the amplitudes are identical and the vectors are in phase, doubling the value of the individual vectors and effectively doubling the output capability of the individual amplifiers. Amplitude and phase errors due to the mismatch of the components degrade the output because the magnitude of the sum vector at an offset angle is less than that of an in-phase vector.
The actual output power capability of this real device can be determined by laying the larger vector (B) on the abscissa and breaking the other vector (A) into its quadrature components (Asinq and Acosq). Summing the two vectors produces two quadrature components, Asinq and B + Acosq. The magnitude of the vector sum is the square root of the sum of the squares of each of the quadrature components.
Multiplying the individual terms yields:
Simplifying the results gives:
If B is the normalized vector, B = 1, the magnitude of the voltage vector with respect to the ideal system will be:
The output power can be represented as the square of the voltage:
A2 is the equivalent power of the A vector:
Substituting PA for A2 and factoring out 2(1+PA) yields:
In a perfect system, vector A is equal to vector B and PA = 1 and Pout = 4. Therefore, the normalized output power, i.e. with respect to the initial input signal is Pnor:
Parameter Pnor in dB
nor(dB)> is the normalized loss due to amplitude and phase mismatches:
where the loss due to unequal signals is Psig(dB):
and the added loss due to amplitude and phase mismatch is ΔP(dB):
These equations break power-combining errors into two categories leading to three power combining error curves:
- The total power for two unequal signals (zero phase error).
- The loss due to phase and amplitude mismatch with respect to the sum of two unequal signals in phase (Fig. 1) .
- The total power loss due to unequal signals and phase mismatches with respect to two equal signals that are in phase at the maximum output power level (Fig. 2 and Fig. 3) .
In power combining, the signal of interest is split into two equal paths, amplified, and combined. If one channel has more loss than the other, the total output power will be lower than expected, where Psig(dB) is the loss with respect to two signals at the maximum power level:
Page Title
Often, technical literature considers only combiner losses, i.e., equal signals going into the combiner, and omits this factor. In designing parallel amplifier systems, the gain into the output combiner should be aligned such that the signal-levels are equal going into the outputcombiner; any errors in this alignment will degrade the signal level. The graphs in Fig. 4 and Fig. 5 relate the normalized output power of two unequal signals to the output power if the signals were equal at maximum amplitude. The curves relates the combining loss to the difference in signal power levels and phase error of the respective signals with respect to the total power if the two signals were in phase. This loss is in addition to the total power loss of two unequal signals that are in phase:
In a typical receiving system, RF signal selection is accomplished by tuning a local oscillator (LO) to within one IF frequency of the desired RF carrier. The resultant signal is a frequency translated RF spectrum to an IF spectrum.
When the LO signal converts an RF signal (at frequency FRF ) to an IF (FIF = FRF- FLO), the image signal (FImage = FRF - 2FIF) is converted to the same IF (FIF = FLO - FImage). If the image is not filtered out, the two signals from different parts of the RF spectrum fold into the same IF spectrum.
Image-rejection mixers are one means of solving this problem. The image is rejected by utilizing the fact that the converted RF signal above the local oscillator is 180 deg. out of phase with the converted RF signals below the same LO. Image-rejection mixers (Fig. 6) direct the RF signal above the LO to one IF port and direct its image (RF signal below the LO) to the other IF port. If the conversion process produces signals equal in amplitude and 180 deg. out of phase, the image rejection will be theoretically infinite. In the real systems, however, signal vectors accumulate amplitude and phase errors throughout the conversion process. The image can be determined by laying vector B on the abscissa and assuming vector A is the smaller vector with a phase error θ.
Image rejection as a ratio of the desired signal is determined by subtracting vector A from vector B and related the result to the sum of the two vectors. To perform the vector addition and subtraction, Vector A is broken into its quadrature components (Asinθ and Acosθ ) and added or subtracted from vector B.
Subtracting the two vectors (Vdiff) produces two quadrature components, (-A Sin θ) and (B-A Cos θ) and adding the two vectors (sum) produces two quadrature components, (Asinθ and B+ Acosθ ). The magnitude of the resultant vectors is the square root of the sum of the squares of each of the quadrature components.
If vector B is the normalized vector with a unity magnitude the results are as follows:
Expanding the square terms yields:
Combining terms results in the following:
The normalized image rejection ( Vimage) is Vdiff/Vsum:
The normalized power (Pimage) is the square of the voltage:
The following graphs plot image rejection as a function of amplitude and phase errors. Figure 5 is a plot of image rejection as a function of phase for different levels of amplitude mismatch. Figure 6 is a plot of image rejection as a function of amplitude mismatch for different levels of phase error. The power-amplifier combiner and image-rejection plots give the design engineer a visual means of determining the component trade-offs and systems specifications. It is interesting to note that power combining is the summation of two large signals and tends to be more forgiving than image rejection, which is the subtraction of two large signals to ideally a null. An acceptable loss of 0.5 dB for combining two signals is realized with a phase error of 20 deg. and an amplitude mismatch of 0.7 dB where as a usually acceptable image rejection of 20 dB, requires a phase error less than 10 deg. and an amplitude error less than 0.5 dB, through a more complex array of components. Most successful image-rejection mixers are integrated as a single component.
REFERENCES
- Frederick H. Raab, Peter Asbeck, Steve Cripps, Peter B. Kenington, Zoya B. Popovic, Nick Pothecary, John F. Sevic, and Nathan O. Sokal, "RF and Microwave Power Amplifier and Transmitter Technologies," High Frequency Electronics, May 2003.
- Bert C. Henderson and James A. Cook, "Image-Reject and Single-Sideband Mixers," Watkins-Johnson Co., Tech-Notes, May/June 1985.