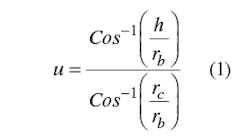Sliced Coaxial Cables Form Compact Couplers

Coupled sliced coaxial cables can provide signal coupling in a compact form factor for 50and 75-W systems. With the ready availability of accurate computer-aided-engineering (CAE) tools, it is possible to apply some basic formulas for calculating the dimensions of these structures to achieve a desired amount of coupling on different substrate materials. What follows is a straightforward approach to calculating those dimensions and analyzing coupler designs fabricated with coupled sliced coaxial cables.

The analytical expressions of coupled sliced coaxial cables can be deduced from rigorous analyses using finite-element-method (FEM) analysis^1,2 and curve-fitting techniques. An analysis can be readily implemented in modern CAE software tools for the design of microwave and wireless components. This study presents accurate and suitable general expressions for all coupled sliced coaxial cables with a coupling coefficient between 10 and 40 dB and a range of dielectric constant from 1 to 10 for a desired impedance of 50 Ω and dielectric constants from 1 to 5 for a desired impedance of 75 Ω. A microwave coupler will be designed to demonstrate the usefulness of these design equations.

A directional coupler with a coupled line composed of a pair of shaped, cut coaxial cables has been analyzed and tested previously in ref. 3. This kind of coupler has excellent performance in terms of high directivity, low VSWR, good isolation, excellent electromagnetic-interference (EMI) shielding, high power handling capability, and low cost due to the use of commercial semi-rigid coaxial cables and elimination of a mechanical housing.^4,5

Figure 1 shows the cross-section of a coupled line with sliced coaxial cables. The cable is assumed to be loss-less with an inner conductor of radius r_c and an outer conductor of radius r_b. Dielectric material with dielectric constant ε_r fills the inside of the cable. A portion of each cable is cut out and two of these cut cables are used to form the coupled line. The cut depth is represented by h on the cross section and is given by Eq. 1:

A variety of techniques are available to accurately determine the dimensions of the sliced coaxial cable.^1,2 These approaches are time-consuming, however, and too tedious for use in circuit design, where closed-form analytical models are to be preferred. By applying FEM analyses along with curve-fitting strategies, it is possible to develop closed-form expressions for determining the dimensions of the sliced coaxial cable with a coupling coefficients between 10 and 40 dB using substrate materials with a range of dielectric constants from 1 to 10 for a desired impedance of 50 W and materials with a range of dielectric constants from 1 to 5 for a desired impedance of 75 Ω.

Figures 2 and 3 show numerical results for sliced coaxial cables with the cut depth (u) as a function of dielectric constant (ε_r) with coupling coefficient (k) as a parameter, as determined by the FEM approach^1,2 for desired impedances of 50 and 75 Ω, respectively.

Derivation of the closed-form expressions for the sliced coaxial cables dimensions is as follows. The cut depth (u) of the sliced coaxial cable can be expressed by Eq. 2:

where:

In Eq. 2, for a characteristic impedance of 50 Ω:

α= 1.2174 – 0.0373k + 2.9734 X 10^–4 k²

ß= –0.0153 + 0.0023k – 7.5428 X 10^–5 k² + 7.7111 X 10^–7 k³

In Eq. 2, for a characteristic impedance of 75 Ω:

α= 1.2064 – 0.0375k + 3.1327 10^–4 k²

ß= –0.0258 + 0.0041k – 1.2334 X 10^–4 k² + 1.1111 X 10^–6 k³

For desired dielectric constant and coupling coefficient values, Eq. 2 permits the calculation of the cut depth of the sliced coaxial cables. Figures 2 and 3 offer comparisons between analytical and numerical results. The close agreement of the results indicates good accuracy of the closed-form expressions for the sliced coaxial cables dimensions.

The conductor radius ratio, r_b/r_c, of the sliced coaxial cables can be calculated from Eq. 3:

where:

Z_c = the characteristic impedance of the sliced coaxial cables.

The ratio h/rb can be deduced from Eq. 1.

Figure 4 presents the structure of a directional coupler using the coupled line with cut coaxial cables. All of the coupler's ports are matched to 50 Ω. The fixed parameters of the coupler include a characteristic impedance of 50 Ω, desired coupling coefficient between the two lines of 20 dB, and an operating frequency of 5 GHz.

Page Title

The coupling line obtained from the proposed relationship features a dielectric constant of 2.03, a cut depth, u, of 0.603, a radius ratio, r_b/r_c, of 3.278 a ratio h/r_b of 0.724, a coupler length of 10.528 mm, and even- and odd-mode characteristic impedances, Z_oe and Z_oo, respectively, of 56.48 Ω and 46.94 Ω.²

The inductance matrix appears as²:

While the capacitance matrix appears as²:

The resulting scattering parameters (S₁₂ for coupling and S₁₄ for isolation) that were obtained using an adapted numerical model⁶ are plotted from 1 to 10 GHz in Fig. 5. The results indicate

that the target desired coupling of 20 dB is achieved from 4 to 6 GHz, with minimum directivity of 25 dB.

In summary, the closed-form equations presented here provide accurate calculations for the dimensions of coupled sliced coaxial cables used for microwave couplers at characteristic impedances of 50 or 75 Ω. These expressions deduced from the finite element method are valid in a wide range of values for the coupling coefficient and the dielectric constant. The formulas were used as the basis for designing a directional coupler, which delivered 20 dB coupling at 5 GHz.

REFERENCES
1. N. Ben Ahmed and M. Feham, "Finite element analysis of RF couplers with sliced coaxial cable," Microwave Journal, Vol. 43, No. 11, November 2000, pp 106-120.
2. N. Ben Ahmed and M. Feham, "Rigorous analytical expressions for electromagnetic parameters of transmission lines: Coupled sliced coaxial cable," Microwave Journal, Vol. 44, No. 11, November 2001, pp 130-138.
3. H. An, O. Monti, R.G. Bossio, and K. Wu, "A novel type of low cost high performance coaxial cable coupler," 25th European Microwave Conference (EuMG'95), 1995.
4. H. An, R.G. Bossio, and K. Wu, "Ultra wide band directional couplers with coaxial cable," Canadian Conference on Electronics And Computer Engineering, 1995.
5. H. An, T. Wang, R.G. Bossio, and K. Wu, "Accurate closed form expression for characteristic impedance of coupled line with sliced coaxial cable," IEE 1995.
6. A.R. Djordjevic, D. Darco, M.C. Goran, and T.K. Sarkan, Circuit Analysis Models for Multiconductors Transmission Lines, Artech House, Norwood, MA, 1997.