7 Ways to Attack Dynamic-Range Measurement Threats

Download this article in .PDF format
This file type includes high resolution graphics and schematics when applicable.

By enhancing the dynamic range of a spectrum/signal or network analyzer, an instrument can discover signals well below its typical noise floor. However, every technique requires a tradeoff in other performance parameters.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F1

1. Dynamic range has a fluid definition that depends on the method of noise-floor description. In contrast, spurious-free dynamic range is easily defined between the highest energy points of the signal and dominant harmonic spur.

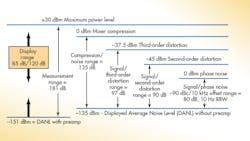
Component and test-equipment manufacturers use various definitions for dynamic range. In essence, dynamic range represents the lowest to highest signal power that a device can operate with or receive (Fig. 1). According to the simplest definition, dynamic range spans the noise floor to the peak power level that can be handled by the receiver while remaining linear.

Several different methods exist for measuring noise floor and how nonlinear—or deep into compression—the receiver can be driven. Developing a solid understanding of the challenges involved in obtaining significant dynamic range, and the methods for enhancing a test’s dynamic range, helps engineers fully exploit today’s test-and-measurement instruments.

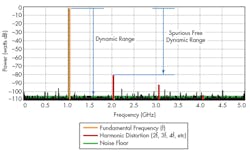
It should be noted that nonlinear distortion products, such as second- and third-harmonic distortion, complicate the definition of dynamic range (Fig. 2). They also limit the lower level at which signals can be received. Among other issues are memory effects, which occur when energy trapped or stored within a portion of the signal chain leads to increased noise factors from residual responses. Phase noise and mixer compression may also affect dynamic range. For test-and-measurement instruments in particular, one limiting factor for dynamic range concerns the display range (in digital instruments, it’s the range of the analog-to-digital converter, or ADC, based on auto-ranging) (Figs. 3 and 4).

Measurement Challenges

Four main challenges confront engineers when trying to achieve a high level of dynamic range:

Broadband Noise and Noise Floor

A large number of broadband and narrowband noise generators exist in a real-world system. (Here, noise is generally described as anything other than the signal that you desire.) Narrowband noise generators are often deemed interference. Yet broadband noise generators, such as thermal noise, are considered contributors to the noise floor. Noise floor—the power level at which an instrument cannot distinguish a desired signal from the broadband noise—can be measured using one of a handful of variables: root mean-square (RMS) values, mean value of the linear magnitude, mean value of the log magnitude, the lowest noise level, or the peak noise level of the broadband noise.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F2

2. Depending on the noise generators in an environment, effects like compression, harmonics, and phase noise could be the limiting factors in the dynamic range of a measurement.

Phase Noise and Noise Distortion

Phase-noise contributions from either the instrument or the device under test (DUT) combine with the system’s broadband noise to increase the effective noise floor. Phase noise also can mask distortion products and increase measurement inaccuracies, as it spreads the signal’s sidebands beyond the resolution bandwidth (RBW). This latter effect will ultimately limit the narrowness of the RBW setting used to reduce the noise floor.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F3

3. To achieve the highest dynamic range, the mixer level should be set so that the noise and harmonic intercepts are at their lowest point.

On a dynamic-range chart, phase noise increases the displayed average noise level (DANL) and distortion relative to the mixer level (Fig. 5). The broadband and phase noise affect the distortion products as they do the desired signal. Distortion noise appears on a dynamic-range chart as a web between the noise line and the second- and third-order distortion lines. Ultimately, phase noise impacts both the signal-to-noise ratio (SNR) and the spurious-free dynamic range (SFDR). It is somewhat misleadingly reported in a spectrum-analzyer display, because the displayed signal also includes the broadband noise power and phase-noise variations.

Mixer or Reference Level

For highly linear DUTs, maintaining a low mixer level will keep the mixer’s distortion products under the DUT’s distortion level. Although it may not impact the DUT’s linearity, a lower mixer level does reduce overall dynamic range and the relative height of the noise floor at the front end of a spectrum/signal analyzer (Fig. 6).

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F4

4. Averaging over a narrower bandwidth can reduce noise-level measurement in the device. This approach enhances dynamic range at the cost of slower sweep speeds.

Dynamic range can be maximized by keeping the mixer level low enough to avoid compression and cause distortion. At the same time, the power input into the mixer must be optimized. Interestingly, the distortion noise shifts the optimum point of the mixer level to achieve the maximum dynamic range. Essentially, the “webbing” effect of distortion noise on a dynamic-range chart shifts the lowest DANL and distortion point relative to the mixer level. They are moved slightly away from the intersection of the noise and harmonic distortion lines.

Second- and Third-Harmonic Distortion

DUT or instrument nonlinearities can induce harmonic distortions that impact the signal’s dynamic range. Therefore, one should consider second-order and two-tone third-order harmonics. The greater nonlinear response of a mixer, instrument, DUT, or preamplifier will no doubt increase the strength of the harmonic distortion signals.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F5

5. Phase noise adds degradation to dynamic rangeâeven at optimum mixer levelsâfor noise and harmonic content.

Effectively, this scenario limits the test’s dynamic range with respect to the harmonic spurs. This is commonly referred to as SFDR, after the spurious frequency content of the harmonic distortion. The system’s broadband and phase noise also contribute to the power level and frequency spread of the harmonic signals, exacerbating degradation of the dynamic range. If the RBW is significantly narrow compared to the frequency spread of the spurs’ sideband, it could trigger amplitude errors.

Download this article in .PDF format
This file type includes high resolution graphics and schematics when applicable.

Solutions that Measure Up

Download this article in .PDF format
This file type includes high resolution graphics and schematics when applicable.

Clever engineers continue to discover and design methods to minimize or knock down those dynamic-range measurement hurdles. Seven approaches particularly stand out:

Averaging or Smoothing

For many signals, the noise floor and noise contribution to the signal power vary randomly. As a result, taking the accumulated average of multiple measurements can reduce the variance in the signal response while decreasing the noise floor. The number of sweeps and sweep time scales with the amount of averaging, though. In contrast, smoothing uses an average of adjacent points of the pre-formatted data, reducing peak-to-peak noise in a way that’s similar to video filtering. Smoothing cannot reduce the noise floor.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F6

6. Performing VNA calibration at power levels where the receiver may reach its compression point will add nonlinear effects to the calibration reference.

Point or trace averaging typically embraces one of two methods. Bucket, or point averaging, accumulates and averages the measured results over many sweeps at a single point or bucket. Averaging, in contrast, generally reduces the variance of the measurement, and can be coupled with other methods to increase dynamic range. Averaging also helps compensate for several other noise-reduction techniques that have a tendency to exacerbate the amplitude, phase, and frequency variance.

RBW Reduction

When a narrower resolution bandwidth is used with a signal analyzer, it decreases the 3- and 60-dB bandwidth. This, in turn, increases the frequency resolution and drops the average noise level. With higher-frequency resolution and a lower average noise level, one can observe lower-power signals—albeit in a limited bandwidth.

If the sidebands of modulated signals extend beyond the RBW setting, however, limiting the RBW bandwidth could degrade measurement accuracy. Reducing the signal analyzer’s RBW may diminish the noise contribution that’s internal to the instrument, as well as the system noise. If information on the device’s noise performance is of interest, this method will also cut the apparent noise level of the signal, along with the signal analyzer’s displayed average noise level (DANL). An additional drawback of decreasing the RBW is increased measurement sweep time (Tables 1 and 2).

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F7

7. If the receiver of a VNA is calibrated in the compression region, the nonlinear calibration reference will exacerbate the error of the measurement system.

When working with continuous-wave (CW) signals, it’s critical to compare the resolution bandwidth to the width of the display bucket. If the display bucket is greater than the RBW, a CW signal’s peak will suffer a scalloping error. To reduce the variance, a “normal” detector can be used with a narrow video-bandwidth (VBW) setting along with trace averaging. Care must be taken to avoid averaging the residual phase noise, amplitude modulation, or frequency modulation, thus spreading the signal beyond the RBW.

Noise Correction

Noise correction is another feature designed to enhance a signal analyzer’s noise-floor response. To lower the noise floor, one would measure or model the instrument’s noise power and subtract from the total measured noise power. This effect can significantly increase the dynamic range, depending on the signal analyzer’s noise power.

Dynamic-range benefits were possible with older methods, but noise measurements had to be performed within every measurement cycle. The latest correction method exploits key noise characteristics that are measured during the manufacturer’s calibration. With those measurements, it creates a noise model that can be actively subtracted from the measured noise power in real time.

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F8

8. The internal coupler bypass eliminates the couplersâ insertion loss, effectively increasing VNA dynamic range under specific test circumstances.

The repetitive measurement-and-noise-correction approach remains the most accurate method of removing internal noise and increasing the low end of the dynamic range (Fig. 7). Neither noise-correction method can completely remove the instrument’s noise contribution—the exact contribution is not known. Unfortunately, noise correction does raise the uncertainty around the processed measurements and their variations. Fortunately, averaging can mitigate some of the variance introduced by noise correction.

Segmented Sweep

Some network analyzers carry an option that subdivides a frequency sweep into several segments with its own measurement parameters. The segmented sweep’s adjustable parameters include the number of sweep points, start/stop frequency, RBW, and source power level. This method can adjust the RBW more widely during high-power signals and lower it during low-power signals. Segmented sweeping enhances the sweep speed while maintaining a high dynamic range for DUTs that require simultaneous high-power and low-power measurements in different frequencies.

Configuring Test-Port Source Power Level

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E F9

9. A well-balanced balun/transformer placed in the front end of a differential analog-to-digital converter can reduce the second harmonics in the ADC output. (Courtesy of Marki Microwave)

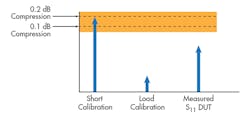
When a network analyzer is calibrated, any nonlinearity in the receiver response will introduce inaccuracies during measurement. This concept becomes especially critical when adjusting the network analyzer’s power level for optimum dynamic range. Ideally, the network analyzer’s signal power level should be substantially below the 0.1-dB compression point to avoid linearity errors. A DUT’s insertion loss may reduce the source power to less than the 0.1-dB compression point of the receiver. During a full calibration, however, the short calibration will induce reflections that may push the signal power beyond the 0.1-dB point, which results in linearity errors. Note that test-cable losses can also be considered when calculating the optimal source power level, as these cables are present in both calibration and testing.

Network Analyzers with Direct Receiver Input

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E Table 1

A receiver’s couplers can be bypassed in specific testing applications, and in network analyzers with a direct receiver input. This approach eliminates the coupler’s losses in the signal chain. The direct-access loop approach can reduce insertion loss to the receiver beyond 10 dB. In doing so, it enhances the test system’s noise-floor performance. If direct access to the source power is available, it may be amplified to enhance the power observed by the DUT (Fig. 8). As a result, the signal level seen at the receiver may rise.

Care must be taken to avoid compressing the receiver with a power signal that wouldn’t drive the receiver into compression under non-bypassed conditions. Port mismatch is another consideration when bypassing network-analyzer couplers. A full calibration may not be performed in some testing situations, which may lead to mismatches that increase measurement uncertainty.

Use of Quality Baluns or Transformers

Mwrf Com Sites Mwrf com Files Uploads 2015 02 22 E Table 2

Many applications that require digitized signals used ADCs. With high-speed ADCs, the converter’s nonlinear response induces harmonic responses in its output. In this case, it’s possible to enhance the dynamic range of a differential ADC and reduce the second harmonic spur’s SFDR limitation (Fig. 9).

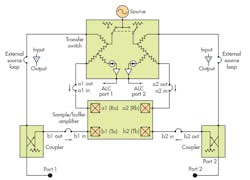
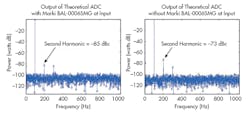
Essentially, a well-balanced balun/transformer can be placed in the signal chain before the ADC. It’s critical to ensure that the phase balance of the balun/transformer is as tight as possible. After all, any phase imbalance will induce distortion that’s proportional to the squared amplitude of the input signal. This technique obviously limits the converter’s frequency response to the bandwidth of the balun/transformer. Any insertion or return loss introduced by the balun/transformer will shrink dynamic range while increasing distortion.