Predict PLL Reference Spurs

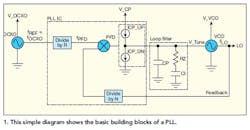
Figure 1 shows the building blocks of a PLL system used for generating an LO signal. The PLL integrated circuit (IC) usually contains the reference (R) and feedback (N) dividers, the phase/frequency detector (PFD), and the charge pump, represented by the two current sources, ICP_UP and ICP_DN. The VCO output is compared to the reference clock (such as the OCXO output) after both signals are divided down in frequency by their respective integer dividers (N and R, respectively). The PFD block controls the charge pump to sink or source current pulses at the PFD frequency rate, f_PFD, into the loop filter to adjust the voltage on the tuning port of the VCO (V_Tune) until the outputs of the clock dividers are equal in frequency and are in phase. When these are equal, the PLL is considered locked. The LO frequency is related to the reference frequency, f_REF, by the following equation:
f_LO = (N/R)(f_REF)

Figure 1 shows a PLL that is called an integer-N PLL because the feedback divider (the N-divider) can only assume integer values. When this divider can assume both integer and non-integer values, the loop is called a fractional-N PLL. The focus in this article will be only on integer-N PLLs, as different mechanisms are at work in fractional-N PLLs.

A PLL IC contributes its own nonideal characteristics to a system, such as phase noise and spurious content. The PLL system of Fig. 1 acts as a lowpass filter on the reference clock phase noise and as a highpass filter on the VCO's phase noise. The lowpass and highpass filter cutoff frequencies are defined by the loop bandwidth (LBW) of the PLL. Ideally, the LO phase noise follows that of the reference clock converted to the LO frequency (that is, multiplied by N/R) to the LBW and subsequently follows the phase noise of the VCO. The PLL IC's noise contribution elevates the phase noise in the transition area.

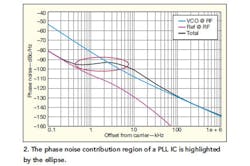
Figure 2 is a phase-noise plot generated by PLLWizard, a PLL design and simulation tool available at no charge from Linear Technology. Figure 2 shows both the total output phase noise ("Total"), and the individual noises at the output due to the reference ("Ref @ RF") and the VCO ("VCO @ RF"). The IC's noise contribution can easily be seen.

Any unwanted signals on the power supplies shown in Figure 1 (V_OCXO, V_CP, and V_VCO) can translate into spurious (spurs) on the LO signal. Careful design of these supplies greatly reduces or even eliminates these spurious signals. Charge pump related spurious signals, however, are inevitable. Still, they can be reduced with careful PLL system design. These spurious signals are commonly referred to as reference spurs, which here refers to f_PFD. An LO signal produced by an integer-N PLL has dual sideband spurious content at f_PFD and its harmonics.

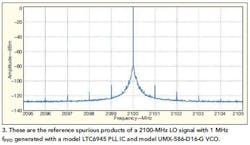
Figure 3 shows the spectrum of a 2.1-GHz LO signal. Here, f_PFD is 1 MHz (N = 2100) and the reference clock is 10 MHz (R = 10). The loop bandwidth is 40 kHz. It is worth mentioning that the spurious level achieved in this measurement is outstanding due to the high performance of the LTC6945, which is a low-noise, low-spurious PLL IC from Linear Technology.

In steady-state operation, the PLL is locked and, theoretically, there is no more need to engage the ICP_UP and ICP_DN current sources of Fig. 1 during every PFD cycle. However, doing this would create a "dead zone" in the loop response, as there is a significant drop in the small-signal loop gain (practically an open loop). This dead zone is eliminated by forcing ICP_UP and ICP_DN to produce extremely narrow pulses during every PFD cycle. These are commonly referred to as anti-backlash pulses. This produces energy content on the VCO tune line at f_PFD and its harmonics. The negative feedback cannot counteract these pulses since these frequencies are outside the loop bandwidth of a properly designed PLL. The VCO, then, is frequency modulated (FM) by this energy content, and related spurious products appear at fPFD and its harmonics, all centered around the LO frequency.

Between anti-backlash pulses, the charge pump current sources are off (in tristate mode). Inherently, the charge pump has some leakage current when in tristate mode. Using an opamp in an active loop filter introduces yet another leakage current source due to the opamp's input bias and offset currents. The aggregate of these unwanted currents, whether sourcing or sinking, causes a drift in the voltage across the loop filter and, consequently, in the VCO's tuning voltage. The negative feedback of the loop will correct for this anomaly by introducing a unipolar current pulse from the charge pump once every PFD cycle so that the average tune line voltage produces the correct frequency out of the VCO. The pulses produce energy at f_PFD, which also causes spurious signals to appear centered around LO and offset by f_PFD and its harmonics, as previously noted.

In integer-N PLLs, frequency f_PFD is often chosen to be relatively small because of the system's frequency step size requirements. This means that the anti-backlash pulse width, especially with the present high-speed IC technologies, is extremely small compared to the PFD period. As such, a large leakage current causes the total charge pump pulses to be unipolar and tends to be the dominant cause of reference spurious signals.

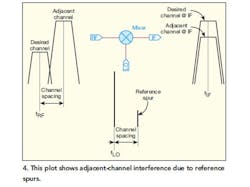
In a particular communications frequency band there are multiple channels that occupy equal bandwidths. The center-to-center frequency distance between two adjacent channels is equal among all channels and is denoted by channel spacing. Due to several factors, it is common to find large variations in signal strength between any two adjacent channels. Figure 4 shows a typical scenario in a multichannel wireless communications system, whereby a stronger channel exists adjacent to a desired but weaker channel.

In an integer-N PLL, f_PFD is usually chosen to be equal to the channel spacing, which means that the reference spurious signals are positioned at the channel spacing from the LO. These spurious signals translate all adjacent and nearby channels to the center of the intermediate frequency (f_IF) signal along with the LO mixing the desired channel to the same frequency. These undesired channels appear as an elevated noise floor to the desired signal and limit the signal-to-noise ratio (SNR).

The mathematical prediction of a PLL IC's phase-noise contribution is relatively straightforward and can be accurately determined by calculations. However, the prediction of reference spurious levels is traditionally believed to be complex. This section derives a method to accurately predict reference spur levels due to leakage current using simple calculations.

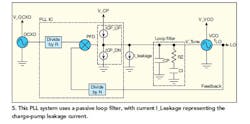
Figure 5 shows a PLL system with a typical passive loop filter along with a current source denoted I_Leakage to represent the leakage current of the charge pump. Assuming the PLL is locked, I_Leakage reduces the charge held by capacitor C_P during the time when the charge pump is off. When the charge pump turns on once every PFD cycle, ICP_UP replenishes the charge lost from C_P by applying a short pulse of current. Feedback forces the average voltage seen at V_Tune (V_Tune_Avg) to be constant, maintaining the correct LO frequency. Figure 6 depicts this.

Page Title

The derivation of the resultant spurious signals involves some knowledge of loop stability requirements, the first being LBW restrictions. The LBW of the PLL system is designed to be at least 10 times smaller than f_PFD:
LBW = f_PFD/10.

Thus, the period of the PFD is:
T_PFD = 1/f_PFD

and hence:
LBW = 1/10T_PFD.

To create a stable loop with plenty of phase margin, a zero, consisting of resistance R_Z and capacitance C_I in Fig. 5, is inserted in the loop at about one-third the value of the LBW. That is:
Zero Location LBW/3 = 1/2pt_Z ? LBW 3/2pt_Z, where t_Z = R_ZC_I

Replacing LBW in the last equation with its equivalent in terms of the phase/frequency detector time period, T_PFD, results in:
3/2pt_Z = 1/(10T_PFD) or T_PFD = (2p/30)t_Z

This means that the PFD period is almost five times shorter than the time constant of the zero, t_Z. The implication is that the ripple produced at a period of T_PFD across C_P is mostly unseen by C_I. The closed-loop bandwidth LBW is approximately equal to the unity crossing of the open-loop gain. Since the zero is located within the loop bandwidth (it is located at one-third the unity crossing of the open-loop gain), the voltage across C_I is dictated by the negative feedback and is mostly a DC value. Practically speaking, only C_P is discharged and charged during the PFD cycles shown in Fig. 6.

If a capacitor, C, is charged or discharged with a constant current source, I, over a period of time given by ?T, the voltage delta across this capacitor is given by:
?V = I(?T/C)

To maintain a fixed output frequency at LO, the voltage droop that occurs during the discharge period is equal to the voltage buildup during the charging period of Fig. 6. That is:
V_Pk-Pk = I_Leakage(T_Discharge)/C_P= I_CP(T_Charge)/C_P

where:
T_Charge = the amount of time the charge pump current is active during every PFD cycle.

The charge pump current, I_CP, is usually in the mA range and leakage current, I_Leakage, is usually in the nA range, which means that:
T_Charge << T_PFD and T_Discharge T_PFD

This implies that the ripple voltage seen across C_P can be represented by a sawtooth waveform.

To study the effect of this sawtooth waveform on the spectrum of the LO signal, and since the waveform is a periodic function, it can be broken down into its frequency components using Fourier Series analysis:

Figure 7 shows an example implementation of an active loop filter built around an opamp. Current I_Leakage represents the combined leakage currents of the charge pump and the opamp. The same methodology used in the passive filter example applies here since the loop filters have a similar structure. The addition of the pole composed of R_P2 and C_P2 at the output of the opamp to limit the device's contribution of noise beyond 15 or 20 times the LBW reduces the amplitude of the sawtooth signal seen at the tuning node of the VCO. It should be noted that capacitance C_P2 includes the input capacitance of the VCO tuning port.

The sawtooth signal undergoes lowpass filtering, the equation for which can be found using basic voltage division equations in the Laplace Transform domain, and can be written as:
|V_Tune/V_Filt| = |1/(1 + j2pfR_P2C_P2)|

where:
f = frequency (in Hz).

Naturally, the sawtooth signal Fourier Series components get affected differently according to their frequency. The reference spur-to-carrier ratios become:
Ref_Spur_Fund/Carrier = 20log₁₀VCOI _Leakage|V_Tune/V_Filt|₁/2_pC_Pf_PFD²> dBc

where:
|V_Tune/V_Filt|₁ = |1/(1 + j2_pfPFDR_P2 C_P2|

Ref_Spur_2ndHar/Carrier = 20log₁₀VCOI_Leakage |V_Tune/V_Filt|₂/8pC_Pf_PFD²> dBc

|V_Tune/V_Filt| = |1/(1 + j4pf_PFDR_P2C_P2|
and so on.

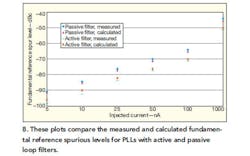
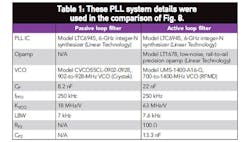
The PLL systems shown in Figs. 5 and 7 were reproduced in the laboratory. External current was introduced at the charge pump node using a precision source meter to null the intrinsic fundamental reference spur caused by inherent leakages in the system. Then, specific additional current values were injected into the loop while measuring the fundamental reference spurious levels.

Figure 8 compares the measured and calculated values for both filter types. The measured and calculated numbers agree to within the instrument accuracies and component tolerances. Table 1 presents more details about the PL systems used for the measurements of Fig. 8.

Table 2 summarizes the equations derived in this article.

Integer-N PLL operation and nonidealities are important topics in the design of RF systems. Reference spurious signals can have a significantly negative impact on overall system performance. Thus, a simple yet accurate model to predict reference spurious levels can be a useful tool.

Appendix: Narrowband FM Equations Derive Spurious/Carrier Ratio

Consider an FM signal centered at an LO of frequency f_c in Hz. This signal can be written as:
e(t) = E_ccosct + ?(t)>,

where:
E_c = the peak amplitude of e(t) (in V).

The instantaneous frequency of e(t) is:
?_inst = (d/dt)ct + ?(t)> = 2pf_c + ?'(t) rad/s

Since e(t) is an FM signal, the modulating signal e_m(t) modulates the instantaneous frequency of e(t) as follows:
?'(t) = Ke_m(t) (in rad/s)

where:
K = the deviation sensitivity of frequency :