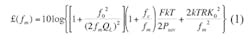Method Minimizes Noise In VCXOs

Frequency reference standards are essential to achieving frequency accuracy and phase stability in electronic systems. Such sources require low phase noise and excellent frequency stability. But requirements for modern systems are also pressuring designers to reduce the size and cost of these reference standards, creating a set of conflicting requirements. Fortunately, a patented approach^1-16 for voltage-controlled crystal oscillators (VCXOs)even those with relative low quality-factor (Q) resonatorshelps achieve excellent phase noise and frequency stability.

A typical oscillator consists of a tuned circuit and an active device, such as a transistor. Ideally, the tuned circuit provides a high loaded Q, generally from less than 100 for simple circuits to more than 1 million for crystal-resonator-based circuits. Noise arises from the active device as well as from resonator losses. The filtering effect of the resonator tends to remove device noise, with higher Qs delivering greater filtering effects. The Leeson equation, which relates these noise effects,¹⁷ was modified by Rohde for use with VCOs¹⁸:

where :

(f_m) = the ratio of sideband power in a 1-Hz bandwidth at f_m to total power (in dB);
f_m= frequency offset;
f₀ = center frequency;
f_c = flicker frequency;
Q_L = loaded Q of the tuned circuit;
F = noise factor;
kT = 4 x 10^-21 at 300 K;
P_sav = average power at oscillator output;
R = equivalent noise resistance of tuning diode (typically 50 O - 10 kO; and
K₀ = oscillator voltage gain;

Equation 1 is limited by the fact that Q_L typically must be estimated; the same applies to the noise factor. The following equations, based on this equivalent circuit, are the exact values for P_sav, Q _{L,and F}, which are required for solving Leeson's equation. Figure 1 offers some insights into the novel noise calculation approach by means of a simplified Colpitts oscillator.¹⁹

From ref. 19, the noise factor can be calculated by Eq. 2, and simplified to Eq. 3 by approximation.

Figure 2 and Figure 3 illustrate the dependency of the noise factor, F, on feedback capacitors C₁ and C₂. From Eq. 1, the phase noise of the oscillator circuit can be minimized by optimizing the noise factor terms as given in Eq. 3 with respect to C₁ and C₂.

Equation 4 can be found by substituting 1/_re for Y₂₁+ (the plus sign denotes large-signal Y-parameter):

When adding an isolating amplifier, the noise of an oscillator circuit is determined by Eq. 5, where:

G = the compressed power gain of the loop amplifier; F = the noise factor of the loop amplifier; k = Boltzmann's constant; T = temperature (K); P₀ = the carrier power level (W) at the output of the loop amplifier; f₀ = the carrier frequency (Hz); f_m= the carrier offset frequency (Hz); Q_L = (pF₀t_g) = the loaded Q of the resonator in the feedback loop; and a_R and a_E = the flicker noise constants for the resonator and loop amplifier, respectively.

To calculate Q_L in Eq. 1 and Eq. 5, it is necessary to consider the unloaded Q (Q₀) and the loading effect of the active device circuits and tuning networks, and so the influence of large-signal Y-parameter Y₂₁ + must be considered. The inverse of Y₂₁ + is responsible for the loading and reduction of the resonator Q (see Eq. 6).

Based on the transformation of the loading of the device emitter's differential impedance (resistance), it is possible to calculate the noise factor of the transistor under large-signal conditions.

Given an ideal resonator, a tuning circuit would not be needed to correct for these shortcomings. But in practical applications, correction is needed. In VCXO circuits, this is achieved through the use of tuning diodes with capacitance values that change as a function of applied voltage. This allows the designer to make the circuit part of a phase-locked-loop (PLL) system. High-stability, low-phase-noise signal sources typically use a quartz-crystal resonator in a Colpitts oscillator configuration.

Alternatively, a Meissner-type oscillator arrangement also has been used. Since the Colpitts oscillator uses a capacitive voltage divider, the crystal must act as a high-Q inductor, requiring that it is slightly detuned from series resonant condition. Quartz crystals are available with Qs ranging from a low 50,000 to several million. Since they are mechanical resonators driven by the piezoelectric effect, they have fundamental-frequency, third-harmonic, fifth-harmonic, seventh-harmonic, and eleventh-harmonic overtone modes.

Page Title

Unfortunately, undesired mode jumping is also possible even in well-planned circuit design. Special circuitry must be added for a VCXO to remain in a desired operating mode. For example, if the fifth overtone mode is desired, a poorly designed oscillator may jump unexpectedly to the third overtone mode. Typically, a crystal oscillator operates from about 1 to 200 MHz. Higher frequencies are possible, but crystal resonators required for higher-frequency operation become thinner and subject to aging effects.

In designing a high-stability crystal oscillator, some method is required to select a resonant mode of interest while also preventing undesired modes. One simple technique that can be utilized is to maximize the negative resistance generated from the active device network for a given particular mode to yield positive resistance for unwanted modes.

The value of the input impedance Z_in(ω) (looking into the base of the transistor in Fig. 4) is given by Eq. 7:

and from ref. 8, the negative resistance and drive level under steady-state conditions are described for the circuit shown in Fig. 5 by Eq. 8 and Eq. 9:

where:

and I₁(x) and I₂(x) are modified Bessel functions of order 0 and 1, respectively. From Eqs. 8 and 9, resonator current drive level IR(ω) can be decreased by increasing the value of feedback capacitor C₂ (Fig. 5) for a given current I_E(ω), but at the cost of a reduction in the value of negative resistance R_n(ω).

To maintain the same value of R_n(ω) as required to compensate for the resistance loss of the crystal resonator at steady-state oscillation, the value of C₁(Fig. 4) must be reduced. However, there is a practical limitation of the minimum value of C₁, which is to be decided by a specified value of the load capacitance of the crystal resonator, including the oscillator transistor's intrinsic base-emitter capacitor (C_be)(Fig. 4).^20-22 Also, the drive-level parameter determines the overall nonlinearity, which causes amplitude-frequency effect, and degrades the 1/f noise performance.²³

A commercial fundamental-frequency 128-MHz VCXO circuit was used as an example to apply the concept of injection and mode-locking. This can be accomplished by using the mode-coupling (tuning L_m-C_m) at higher-order modes) and phase-injection π(ωΔω) techniques for a given mode-coupling condition and drive level R(ω) (Fig. 6).

In general, coupling capacitor C_V1 supports oscillation (without C_V2 and C_V3), but at the cost of slow start-up performance and required high drive level R(ω)>. The higher-order mode is coupled through output path and feedback to the point where frequency-drive sensitivity of the crystal resonator shows maximum group delay and faster slew rate, resulting in improved stability with reduced I_R(ω).

Self-injection-locking can be realized by phase-injection network. The locking range of the self-injection-locked crystal oscillator can be described in term of maximum change in frequency for a given operating conditions by Eq. 11 and Eq. 12:

where ΔL is the maximum change of the effective inductance of the resonator tank circuit, due to the injection-locking signal (realized via the delay-line phase shifter in Fig. 6) and Δf is the maximum frequency shift possible with the locking range of the crystal oscillator. From Eq. 12, the locking range is proportional to the maximum amount of the change of the inductance caused by the injected locking signal. For a varactor-tuned injection-locked LC oscillator, the locking range can be described by Eq. 13:

where ΔC is the maximum amount of capacitance change of the varactor caused by locking signal.

Page Title

For a given oscillator circuit topology, operating condition, and figure-of-merit, it is important to note that the maximum change of ΔL is higher than ΔC and can be given by Eq. 14:

From Eq. 14, a self-injection-locked oscillator has superior capability to adjust frequency to follow the locking signal, resulting in a comparatively higher locking range compared to an external reference for a given figure of merit. By applying the patented technology detailed here,^1-16 simplified versions of differential and mode-feedback fifth-overtone VCXOs are shown in Fig. 7 and Fig. 8, respectively, with their associated phase-noise plots.

Traditionally, crystal-oscillator optimization has been performed by empirical rather than analytical approaches, leading to trial-and-error techniques to improve phase noise. As an example, the approach shown at 128 MHz is being applied in the development of high-performance VCXOs (Fig. 9) for advanced frequency synthesizers designed and produced at Synergy. Figure 10 compares simulated phase noise for the 128-MHz VCXO with only first-pass optimization and with the best results from these new techniques. The simulated results using Ansoft Designer from ANSYS and ADS from Agilent Technologies were validated with theory and measurements (Fig. 11) using the model FSUP signal source analyzer from Rohde & Schwarz and model E5052 analyzer from Agilent. Figure 10 shows typical phase noise without optimization, with first optimization, and final optimizations to show the improvement in phase-noise performance as outlined in the patents.^5-8

Finally, Fig. 11 shows how the novel phase-injection mode-feedback technique improves VCXO stability and phase-noise performance by 10 to 15 dB. The circuit operates at +5 VDC and 30 mA and is suitable for tunable crystal-oscillator applications.

Synergy Microwave Corp.
201 McLean Blvd.
Paterson, NJ 07504
(973) 881-8800

References

1. U.L. Rohde and A.K. Poddar, "Wideband Voltage Controlled Oscillators Employing Evanescent Mode Coupled Resonators," United States Patent No. 7,180,381, February 20, 2007.
2. U.L. Rohde, A.K. Poddar, and R. Rebel, "Integrated Low Noise Microwave Wideband Push-Push VCO," United States Patent No. 7,088,189, August 2006.
3. U.L. Rohde and A.K. Poddar, "User-Definable Thermal Drift Voltage Controlled Oscillator," United States Patent No.7, 265,642 B2, September 4, 2007.
4. U.L. Rohde and A.K. Poddar, "Low Thermal Drift Tunable Frequency Voltage Controlled Oscillatory," United States Patent No.7, 262,670 B2, August 28, 2007.
5. U.L. Rohde and A.K. Poddar, "Tunable Oscillator," United States Patent No.7, 292,113, November 6, 2007.
6. U.L. Rohde and A.K. Poddar, "Tunable Frequency, Low Phase Noise and Low Thermal Drift Oscillator," United States Patent No.7196591, March 2007.
7. U.L. Rohde and A.K. Poddar, "Low Noise, Hybrid Tuned Wideband Voltage Controlled Oscillator," United States Patent No. 7,365,612 B2, April 29, 2008.
8. U.L. Rohde and A.K. Poddar, "Tunable Frequency, Low Phase Noise and Low Thermal Drift Oscillator," United States Patent No. 7,545,229, June 9, 2009.
9. U.L. Rohde and A.K. Poddar, "Passive Reflection Mixer," United States Patent No. 7,580,693, August 25, 2009.
10. U.L. Rohde and A.K. Poddar, "User-Definable, Low Cost, Low Phase Hit and Spectral Pure Tunable Oscillator," United States Patent No. 7,586,381, September 8, 2009.
11. U.L. Rohde and A.K. Poddar, "User-Definable, Low Cost, Low Noise, and Phase Hit Insensitive Multi-octave-band Tunable Oscillator, Phase Hit and Spectral Pure Tunable Oscillator," United States Patent No. 7,605,670, October 20, 2009.
12. M. Rohde and A.K. Poddar, "Visually Inspectable Surface Mount Device Pad," United States Patent No. 7612296, Nov 3, 2009.
13. U.L. Rohde and A.K. Poddar, "Low Noise and Low Phase Hits Tunable Oscillator," United States Patent No. 7,636, 021, Dec. 22, 2009.
14. U.L. Rohde and A. K. Poddar, "Wideband Voltage Controlled Oscillators Employing Evanescent Mode Coupled Resonators," Canadian Patent No. 2,563, 174, July 21, 2009.
15. U.L. Rohde and A.K. Poddar, "User-Definable Thermal Drift Voltage Controlled Oscillator," Canadian Patent No. 2,548,317, April 21, 2009.
16. U.L. Rohde and A.K. Poddar, "Integrated Low Noise Microwave Wideband Push-Push VCO," Canadian Patent No. 2,548,311, April 14, 2009.
17. D.B. Leeson, "A Simple Model of Feedback Oscillator Noise Spectrum," Proceedings of the IEEE, Vol. 54, 1966, pp. 329-330.
18. U.L. Rohde and T.T.N. Bucher, Communication Receivers Principles & Design, McGraw-Hill, New York, 1988, p. 302.
19. U.L. Rohde, A.K. Poddar, and G. Boeck, The Design of Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, Wiley, New York, 2005.
20. Y. Tsuzuki, T. Adachi, and J.W. Zhang, "Fast Start-up Crystal Oscillator Circuits," 1995 IEEE International Frequency Control Symposium Digest, pp. 565-568.
21. Y Tsuzuki, T. Adachi, and J.W. Zhang, "Form.ulation of Nonlinear Negative Resistance For Calculation of Start-up Characteristics of Crystal Oscillatorstor Circuits," 1996 IEEE International Frequency Control Symposium Digest, pp. 710-713.
22. Y. Tsuzuki, T. Adachi, and H. Yokohara, "Low Drive Level Crystal Oscillator Circuit," 1997 IEEE International Frequency Control Symposium Digest, pp. 966-969.
23. S. Galliou, F. Sthal, and M. Mourey, "Enhanced Phase Noise Model For Quartz Crystal Oscillators," 2002 IEEE International Frequency Control Symposium.