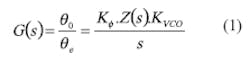Perfect A PLL LTE Synthesizer

Samir Kameche and Mohammed Feham

Mobile communications systems have evolved from handling voice exclusively to providing voice, data, and even video transmissions. This trend began with systems based on wideband code-division-multiple-access (WCDMA) technology developed as part of Third Generation Partnership Project (3GPP) standards and is reaching fulfillment in the successor to those standards, known as Long Term Evolution (LTE) cellular technology. LTE is the first cellular communication system optimized from the outset to support packet-switched data services, within which packetized voice communications are just one part. High-performance frequency synthesis is needed to support LTE systems, with minimal noise characteristics and adequate frequency switching speed. Such a phase-lock-loop (PLL) frequency synthesizer was developed through simulation and analysis, including an accurate transient analysis of the PLL, to achieve output noise spectral density of -101.3 dBc/Hz offset 5 MHz from the carrier and frequency switching time of about 147 s for a frequency jump of 60 MHz.

LTE wireless communications technology is intended to provide high quality of service (QoS) with high broadband bit rates with robust security for different traffic classes.¹ The LTE physical layer is targeted to provide improved radio interface capabilities between the base station and user equipment (UE) compared to previous cellular technologies like universal mobile telecommunications system (UMTS) or high-speed downlink packet access (HSDPA). According to the initial requirements defined by the 3GPP (3GPP 25.913),² the LTE physical layer should support peak data rates of more than 100 Mb/s over its downlink (DL) and 50 Mb/s over its uplink (UL). A flexible transmission bandwidth ranging from 1.25 to 20 MHz will provide support for users with different capabilities. For transmissions in paired and unpaired spectra, the LTE air interface supports both frequency-division-duplex (FDD) and time-division-duplex (TDD) modes.

LTE can be used with both paired FDD and unpaired TDD spectra. Early product releases support both duplex schemes. In general, FDD is more efficient and represents higher device and infrastructure volumes, but TDD is a good complement (by way of example) in spectrum center gaps. Because LTE hardware is the same for FDD and TDD, except for the radio unit, TDD operators will for the first time be able to enjoy the economies of scale that come with broadly supported FDD products. Fifteen different FDD frequency bands and eight different TDD frequency bands have been defined in the 3GPP for LTE use, as shown in Table 1 and Table 2 (see also refs. 3 and 4), and it is likely that more bands will be added.

The PLL is a significant part of any LTE system, since it controls the stability of a high-frequency oscillator by maintaining a constant phase angle relative to a reference oscillator. PLL-based frequency synthesizers can generate a wide range of output frequencies for use by LTE and other wireless communications systems, based on a single stable reference frequency from a crystal oscillator.⁵

A PLL is a feedback control system that compares the phases of two input signals and produces an error signal that is proportional to the difference between the phases of the two signals. The error signal is then processed through a lowpass filter and used to drive a voltage-controlled oscillator (VCO) to produce stable, high-frequency output signals. The VCO's output frequency is fed through a frequency divider back to the input of the system, producing a negative feedback loop. If the output frequency of the VCO drifts, the phase error signal will increase, driving the frequency of the VCO in the opposite direction to reduce the error. In this way, the output of the VCO is locked to the frequency of the other input signal, which is called the reference and is usually produced by a stable crystal oscillator. Figure 1 shows the basic elements of a PLL-based frequency synthesizer. Integer-N PLL frequency synthesizers divide the output frequency by an integer value.

A PLL is a highly nonlinear system,⁶ although it can be described with a linear model when the loop is in lock. A PLL is in a locked state when the phase error signal produced by the phase detector settles to a constant value. This implies that the output signal has the same frequency as the input reference signal. A phase difference between the reference and output signal may exist depending on the type of PLL used. However, this phase difference remains constant while the loop is in lock. If the PLL is used as a frequency synthesizer, the output signal will have a frequency N times the reference frequency.

Figure 2 shows a linear mathematical model representing the phase of a PLL in its locked state,^7,8 where K_f is the phase detector/charge pump gain (mA/rad); Z(s) is the transfer function of the loop filter; N is the main divider ratio; and K_VCO is the VCO gain (MHz/V). The phase of the high-frequency oscillator, θ₀, is compared with the phase of the reference oscillator, θ_r, and adjusted until the difference approaches zero. Parameters θ_i and θ_e represent the opposite and error phases, respectively.

In examining Fig. 2, it should be clear that the output is modeled as a phase and not a frequency. It makes more sense to model the phases and not the frequencies because the phase detector works in term of phase. The VCO gain is multiplied by a factor of 1/S in order to convert it from a frequency to a phase. To help in understanding this modeling in terms of phase rather than frequency, the PLL phase transfer functions are shown in Eqs. 1, 2, and 3 for forward-loop gain, reverse-loop gain, and open-loop gain, respectively:

Combining these transfer functions gives the closed-loop gain in Eq. 4:

Page Title

Figure 3 shows a typical charge pump and passive loop filter arrangement.⁸ It uses a matched current source and sinks together with switches, which direct the currents into and out of the loop filter. Phase differences at the phase detector input produce dissimilar pulse widths on the phase detector "up" and "down" outputs, causing the loop filter voltage to pump up or down as directed.

Equations 5 and 6 give the transfer functions of the second- and third-order loop filters:

where Z(s) describes the transfer function of the second order loop filter given by:

Reference spurious products are also introduced in the simulation. The power levels of these spurious signals are calculated by the closed-loop transfer function evaluated at the spurious offset frequencies, F_spur. In general, spurious signals are caused by either leakage or mismatch of the charge pump. In several studies, F_spur is assumed to be a multiple of the comparison frequency, F_comp.

The power level of the reference spurious signals can be expressed by Eq. 7⁹

LTE is an example of the continuing evolution of cellular technology, developing as it did from UMTS, with each step forward requiring improvements in frequency synthesizer performance and design. The 3GPP WCDMA standard covers a number of other frequency variants in addition to the UMTS core band. Frequency variants operate from 1920 to 1980 MHz for uplink frequencies and 2110 to 2170 MHz for downlink frequencies. The nominal WCDMA carrier spacing is 5 MHz but can be adjusted with a 200 kHz raster according to the requirements of the adjacent channel interference. By using a larger carrier spacing, adjacent channel interference can be reduced.

Advanced Design System (ADS), a commercial microwave simulation program from Agilent Technologies, was used to predict the performance of a frequency synthesizer for LTE applications. Figure 4 shows an ADS simulation block diagram of the LTE synthesizer. Based on that simulation block diagram, simulations were performed for the open-loop gain and phase transfer functions of the PLL (Fig. 5), while Fig. 6 shows the closed-loop gain transfer function. From Fig. 5, it is apparent that the gain drops to 1 (0 dB) at the specified loop bandwidth frequency (10 kHz) while the phase is at its peak of about -125 deg., which corresponds to a phase margin of 55 deg. (180 125 deg.).

In the loop bandwidth of the synthesizer, the transfer function of the closed loop is very large in amplitude (Fig.6), thus causing an increased noise level of reference oscillator. This gain is constant until it reaches the loop bandwidth, then drops rapidly. This function represents also the gain of noise in the bandwidth and the attenuation of this noise above this frequency. The gain in the loop pass band is largely coming from the N division ratio of the loop.

Phase noise is a parameter widely used to describe random fluctuations in the short-term frequency of a signal source. Frequency stability is a measure of the degree to which an oscillator or other signal source maintains the same frequency value for a given amount of time. It is one of the more important parameters in the design of oscillators^10,11. Usually, phase noise is characterized by its spectral distribution, which is a key parameter when characterizing PLLs. To better understand oscillator phase noise, readers can find detailed analyses performed by a number of authors in refs. 12-15.

Page Title

Figure 7 shows the single-sideband (SSB) phase noise contributions of each component constituting the frequency synthesizer and their effects on its RF output. It is clear that the noise is very important inside the loop bandwidth, owing to the fact that the gain of the closed-loop transfer function is high within the loop bandwidth. It should also be noted that the amplitudes of most of the different noise sources decrease within the loop bandwidth, with only the noise of the VCO increasing within the loop bandwidth. Otherwise, it can be seen that contributions to the total phase noise of the frequency synthesizer from its various noise sources are dominated by the phase noise of the reference oscillator.

To create a precise frequency synthesizer design, an accurate estimation of the loop filter was needed. Figure 8 shows the output spectrum for the case of an optimal loop filter design. Simulation results obtained with the MATLAB mathematical modeling software from The MathWorks indicate a noise density of -101.3 dBc/Hz offset 5 MHz from the carrier and a signal-to-noise ratio (SNR) of about 40.72 dB.

In modern telecommunications systems, a synthesizer often has strict requirements for settling time, defined as the time that it takes the PLL to switch between two different frequencies. This is measured from the start of the frequency switching action to the time that the new frequency settles within a specified accuracy. During the time that the PLL switches between two different frequencies, a transceiver can neither transmit nor receive any data until the frequency offset error is acceptable. This reduces the effective data rate that the system can achieve. While the PLL lock time is mainly dependent on the loop bandwidth (the lock time is always inversely proportional to the loop bandwidth), it also depends on the size of the frequency jump during the PLL switching.

Figure 9 shows the evolution of the division ratio N after a frequency jump. From Fig. 9, it was found that the splitting ratio varies between the value of N1 = 422 and N2 = 434i.e., between the frequencies F1 = 2110 MHz and F2 = 2170 MHz. It is also noted that the divider changes its value when it receives a command from the VCO after a time of 0.2 s (the inverse of the comparison frequency), and after it has stabilized during the PLL lock-up period. As Fig. 9 shows, the transition between N1 and N2 for the LTE frequency synthesizer is only about 20 ns.

To visualize the loop locking phenomenon, the evolution of the PFD output voltage can be analyzed as a function of time. As seen in the theoretical study of a PLL, the voltage should fluctuate for some time (the lock-up time of the loop) before stabilizing and becoming constant. Simulation of this event yields the curve shown in Fig. 10. Figure 11 shows the evolution of the current signal of the charge pump during the stabilization of the PLL, and Fig. 12 shows the PLL's transient response. This analysis of the evolution of the instantaneous frequency of the VCO output versus time for a frequency jump of 60 MHz (the full width of the frequency band of interest) follows an adequate optimization of the loop filter.

As expected, the switching time predicted following an envelope simulation with ADS is about 147 s. This value is adequate for LTE in the case where the user equipment (UE) is mobile and changing location. A change in location implies a change in transmission frequency (along with a change in reception frequency), as the mobile device moves throughout the LTE network. If a communication is in progress, the system must switch to the new frequency allocated by the base transceiver station (BTS) to the mobile station without any service interruption.

In summary, this simulation of an LTE frequency synthesizer shows the impact of the loop filter design on the loop stability during an analysis of transient behavior. A closed-loop phase-noise analysis was effective in evaluating PLL single-sideband SSB phase-noise performance by calculating the noise contributions of the various components comprising the frequency synthesizer and the effects of those contributions on the synthesizer's output signal quality. An accurate transient analysis of the PLL system was presented, showing a noise density of -101.3 dBc/Hz offset 5 MHz from the carrier, with a switching time of about 147 s for a 60 MHz frequency jump and an SNR of about 40.72 dB.

SAMIR KAMECHE, Assistant Professor, Electronics and Electrical Engineering Department, STIC Laboratory, University of Tlemcen, Algeria; e-mail: [email protected].

MOHAMMED FEHAM, Professor, Electronics and Electrical Engineering Department, STIC Laboratory, University of Tlemcen, Algeria.

References

1. Stefania Sesia, Issam Toufik, and Matthew Baker, LTEThe UMTS Long Term Evolution, Wiley, London, 2009.
2. 3GPP Technical Report 25.913, "Requirements for Evolved UTRA (E-UTRA) and Evolved UTRAN (E-UTRAN) (Release 7)," www.3gpp.org.
3. 3GPP, TS 25.104, "Base Station (BS) radio transmission and reception (FDD)."
4. 3GPP, TS 25.105, "Base Station (BS) radio transmission and reception (TDD)."
5. R.E. Best, Phase-Locked Loops: Design, Simulation, and Applications, 6th ed. McGraw-Hill, New York, 2007.
6. F.M. Gardner, Phase-lock Techniques, 2nd ed., Wiley, New York, 1979.
7. David Vye,"Performing Transient Analysis on PLL Frequency Synthesizers," Microwave Journal, Vol. 45, No. 1, 2002, pp. 62-79.
8. S. Kameche, M. Feham, and M. Kameche, "PLL Synthesizer Tunes DCS 1800 Band,'' Microwaves & RF, Vol. 46, No. 6, June 2007, pp. 84-90.
9. D. Banarjee, PLL Performance, Simulation, and Design, 4th ed., 2006.
10. D. Ham and A. Hajimiri, "Design and Optimization of a Low Noise 2.4-GHz CMOS VCO with Integrated LC Tank and MOSCAP Tuning," ISCAS-IEEE International Symposium on Circuits and Systems, May, 2000, Geneva, Switzerland, May 2000, pp. 28-31.
11. E. Hegazi, et al., "A Filtering Technique to Lower Oscillator Phase Noise," in IEEE International Solid-State Circuits Conference (ISSCC), 2001, pp. 364-365.
12. L.S. Cutler and C.L. Searle," Some aspects of the theory and measurement of frequency fluctuations in frequency standards," Proceedings of the IEEE, Vol. 54, No. 2, February 1966, pp. 136-154.
13. D.B. Lesson," A simple model of feedback oscillator noise spectrum," Proceedings of the IEEE, Vol. 54, No. 2, February 1966, pp. 329-330.
14. A. Hajimiri and Thomas H. Lee, "A general theory of phase noise in electrical oscillators," IEEE Journal of Solid-State Circuits, Vol. 36, No. 2, February 1998, pp. 179-194.
15. Erich Hafner," The effects of noise in oscillators," Proceedings of the IEEE, Vol. 54, No. 2, February 1966, pp. 179-198.