What's the Difference between Various EM-Simulation Numerical Methods?
This file type includes high resolution graphics and schematics when applicable.
In a closed-loop mathematical system, it often is impossible to represent the complex geometries and boundary conditions of RF/microwave devices and applications. Due to these devices’ diverse material properties and colliding mechanical-electrical properties, however, there is a growing need to grasp, through simulation, their behavior in their actual environments. Computational electromagnetics (CEM) delves into the array of techniques used to efficiently compute approximations to Maxwell’s equations. In doing so, it enables these complex electrodynamic systems to be modeled. While many numerical methods are known to CEM, this article will delve into the numerical methods that are used most commonly in solutions for EM simulation with the latest technologies.
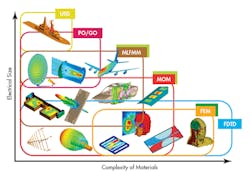
Among the methods used for CEM, for example, are integral-equation solvers, differential-equation (DE) solvers, asymptotic techniques, and other numerical methods (Fig. 1). In the top EM simulation software, which uses integral-equation solving techniques, the methods of moments (MOM) and multilevel fast multipole method (MLFMM) are commonly used. Typically, the numerical methods that use DE solving techniques include the finite-difference time-domain (FDTD), finite-element-method (FEM), and transmission-line-matrix (TLM) methods. In contrast, asymptotic techniques include physical optics (PO), geometric optics (GO), and the uniform theory of diffraction (UTD). The eigen-mode expansion (EME) method is often used for closed resonant systems (Fig. 2).
Integral-Equation Solvers
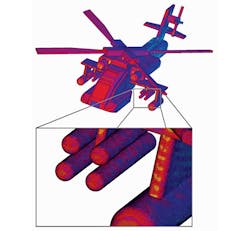
The MOM is performed by solving linear partial differential equations (PDEs), which are formulated as integral equations (IEs). Called boundary integral form, this form gives rise to MOM’s other name—boundary element method (BEM). Many industries, ranging from fluid mechanics to acoustics, use this method. When dealing with problems with low surface-to-volume ratios, the computation using MOM is relatively straightforward and efficient. MOM also can be used for problems in which the free-space Green’s function is calculable. Generally speaking, this means that nonlinearities and non-linearly homogeneous media are difficult to simulate as a function of the boundary conditions’ restrictions. As a result, MOM is most useful for problems with currents on metallic objects, dielectric structures, and radiation in free space (Fig. 3). In addition, it is suited for electrically small dimensions that are predominantly composed of metallic objects.
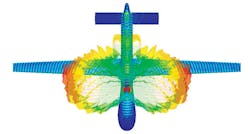
As an alternative to MOM for large electrical scenarios, MLFMM is an integral-equation solver based upon the multipole expansion technique. MOM and MLFMM are similar in that they both model the interaction between triangles with basis functions. In contrast to MOM’s individual interaction-based computation, however, MLFMM computes the interactions of the basis functions in groups (Fig. 4).
Thus, MOM produces a matrix with elements that number as the square of the quantity of basis functions—or impedance matrices—required for the solution. Computation time for MOM scales as the cube of the number of basis functions. In contrast, MLFMM’s logarithmically subdivided groups of basis functions reduce the matrix elements to the number of basis functions multiplied by the logarithm of the number of basis functions. This method reduces computation time to the square of the logarithm of the number of basis functions multiplied by the number of those functions.
These differences enable MLFMM to tackle electrically large structures, such as antennas placed on large vehicles/ships. It also can be used to compute specific-absorption-rate (SAR) levels for possible health hazards near large radiators. For many situations, these BEMs may be drastically less computationally efficient than volume-discretization methods (VDM), such as FEM. After all, the computed matrices for BEMs tend to be fully populated and the computational resources increase as a square of the problem space. With VDMs, however, the matrices are usually just locally connected and the system matrices tend to rise linearly with the increase in problem size.
This file type includes high resolution graphics and schematics when applicable.
Differential-Equation Solvers
This file type includes high resolution graphics and schematics when applicable.
FEM is performed by solving for differential equations using finite differences and other standard techniques. Such techniques are numerically stable approximations of the problem spaces’ partial-differential and integral equations. Generating DEs that are equivalent to the PDEs is critical in preventing cascading errors from accumulating. In order to create these approximated DEs, certain factors—such as the time derivatives—must be eliminated. These simplifications enable the finite-element method to effectively simulate the performance of electrically large and inhomogeneous dielectric systems with complex domains and varying precision over the problem space.
With the full-wave solving technique, FDTD, partial-differential versions of Maxwell’s equations are adjusted to central-difference equations and then discretized. This differential time-domain method solves for the electric field and then the magnetic field (Fig. 5). This is done in two offset rectilinear grids at a certain time. The calculation then progresses across the problem space.
Fourier techniques are used with these computational results to approximate the frequency-domain behavior. It should be noted that time is the varying factor. As long as the time resolution is narrow enough to fulfill the Nyquist-Shannon sampling theorem, the response of a large range of frequencies can be modeled with little computational difficulty. Because FDTD relies on a large amount of simple mathematical operations, graphics-processing-unit (GPU) computation is possible. It can dramatically accelerate computation time. When combined with volume meshing techniques, which use voxels along a non-uniform rectilinear mesh, these factors enable the FDTD method to effectively simulate the behavior of complex systems. Such systems include those comprising non-homogeneous materials or covering wide frequencies of operation, such as biomedical applications and applications using wideband antennas.
There are many 2D and 3D implementations of TLM techniques in lumped-element-circuit and electromagnetic simulators. For instance, the 3D time-domain TLM method is a full-wave and volume-meshing solver of Maxwell’s equations that works locally within space and time. It uses transmission-line nodes within hexahedral cells (Fig. 6). As the solver steps across time, a scattering matrix is developed by mapping the pulse’s incident and reflected at each node. The EM responses are calculated by the S-parameters developed at each node.
TLM methods boast capabilities that are similar to those offered by FDTD methods. Additionally, they can benefit from the lumping of cells, depending on the density of geometric boundaries near the nodes. As is the case with FDTD, wide frequency ranges and electrically large systems can be effectively simulated along with EM compatibility/EM interference (EMC/EMI) phenomena. Examples include lightning discharges and EM pulses.
Some modern simulation software suites use hybridized blends of techniques, such as FEM/MOM and FEM/MLFMM. In doing so, they can take advantage of each technique’s benefits while mitigating its drawbacks. Radiation boundaries are used to separate the problem spaces. Often, differential- and integral-equation methods are combined to take advantage of DE solver-method capabilities of accounting for complex geometries. Another goal is to leverage IE solver-method capabilities of accurately depicting radiating and scattering problems.
These solutions--along with clever computational tricks—can increase the computational efficiency of these methods. For electrically massive problem spaces, however—such as those beyond an order of magnitude greater than the wavelength—the computational resources necessary to accurately simulate the space would be staggering. Here, a third group of CEM methods come into play—namely, asymptotic techniques.
Asymptotic Techniques
Physical optics utilizes ray optics to predict the currents on the surface of a large metallic or dielectric structure. This approach is a high-frequency asymptotic method (Fig. 7). The fields induced by these currents are used to calculate the scattered radiation from the surface of the structures by integrating those fields over the surface. Unlike other asymptotic methods, PO uses full-wave EM physics. Both MOM and MLFMM can be combined with PO for a hybrid solution. Doing so enables a more accurate representation of small geometrics in a vastly larger problem space while maintaining computational feasibility.
Although the uniform theory of diffraction method is similar to PO, it is based on computing the EM scattering of electrically small discontinuities. With UTD, diffraction coefficients are derived from the approximation of near-field (NF) EM behavior, assuming it is quasi-optical and using ray diffraction (Fig. 8). The power and phase of the fields are computed from the discontinuity point and combined with the incident and reflected fields for a complete field solution. UTD is often used to predict transmission paths for high-frequency antennas mounted on large superstructures, which reveals the optimal antenna position. Some simulators combine MOM and UTD methods, as these methods support bi-directional coupling. This capability could aid the simulation of a small antenna structure in close proximity to a much larger structure simulated with UTD.
Geometric optics is a step beyond UTD and PO, in that purely ray optics techniques are used to simulate massive electrically large systems. Optical refraction, reflection, and propagation theory are used to predict the behavior of bouncing rays, which are launched from points designated in the 3D space. GO methods also can account for dielectric coatings of metallic surfaces, anisotropic materials, and multilayer dielectrics. GO is used in situations that induce extreme amounts of multiple reflections, as this application would call for exponentially increased computational resources with UTD or PO methods. Additionally, GO methods are able to account for and even compute radar cross sections. In contrast, the PO and UTD methods are limited in this area. A MOM approach could be taken to the radiating antenna within a much larger space, as the antenna’s effects could be simulated using GO techniques.
This file type includes high resolution graphics and schematics when applicable.