Download this article in PDF format.
The ability to avoid enemy radar requires that modern fighter aircrafts, ships, and missiles have a very small radar cross section (RCS). Researchers and engineers are working on making these stealth objects rely on computational electromagnetics (EM) to optimize the RCS and scattering effects of an arbitrary object using radars. An object exposed to EM waves scatters the incident energy in all directions. The energy that returns to the source of the EM wave, known as backscattering, is the “echo” of the object. The intensity of the radar echo is what we refer to as RCS.
Best practices use a sphere to calibrate radar systems because a sphere will return an echo signal back to the target that sent it. The RCS wavelength consists of three parts: the Rayleigh, Mie, and optical region. The Mie and optical regions are of particular interest, because the analytical solution of the RCS is well-known.
Back to RCS Basics
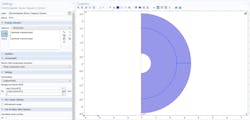
A classic benchmark example of Mie scattering of a sphere is a great place to start when examining this problem. In the following example, a plane wave illuminates a metallic sphere in free space, and its RCS is computed. The geometry consists of two concentric spherical shells (Fig. 1). The innermost shell, adjacent to the sphere, represents the free-space domain, and the second shell represents a perfectly matched layer (PML) region.
1. The norm of total electric field and the time-averaged power flow are visualized with the geometry of a perfect electric conductor (PEC) sphere in free space modeled in COMSOL Multiphysics.
The PML is used to provide an approximate reflection-free termination of the free-space domain. If analyzed with a fine frequency resolution, this can turn into a time-consuming task. Fortunately, when an object is axially symmetric—such as a sphere, which scatters isotropically—the entire 3D object does not have to be analyzed. The cross-sectional blueprint can be sufficient to analyze the EM wave propagation and resonant behavior of the object under certain circumstances.
Size Matters
The RCS characteristics are largely influenced by the electrical size and nature of the target subjected to the radar beam. As the target—the sphere in our case—decreases in size, moving from the optical region to Rayleigh region via the Mie area, asymptotic methods are not accurate enough to capture all of the physical phenomena. To achieve accurate results, we must analyze the problem by solving full-wave equations. Under these circumstances, the computational costs are quite high. To ensure efficiency is prioritized, we take advantage of the 2D axisymmetric approach (Fig. 2).
2. This figure shows background field settings of the scattered field formulation and 2D axisymmetric geometry that includes perfectly matched layer domains.
The variation of the scattered field is minimal for electrically small targets. Alternatively, electrically large targets can result in different RCS characteristics. Let's assume that our sphere is metallic, meaning it will have a high conductivity. For this model, the sphere’s metallic surface is modeled as a perfect electric conductor (PEC).
All of the domain material is defined as a vacuum. The outermost domains are set to the spherical type of PMLs that absorb all outgoing waves. All of the simulation domains are excited by a circularly polarized background field, except for the PML area. The results of this reduced geometry representation are enough to describe the response of the original 3D geometry to the EM waves (Fig. 3).
3. 3D far-field is visualized from a 2D axisymmetric simulation in COMSOL Multiphysics.
Under the Hood of 2D Axisymmetric Modeling
The far-field calculation boundary is specified to compute the scattered field from the sphere illuminated by the background field. We set the azimuthal mode for this 2D axisymmetric model to one. The mesh operation is performed based on the wavelength of the maximum frequency (200 MHz) used in the simulation via the physics-controlled mesh functionality.
Through the physics-controlled mesh, the maximum mesh element size is set to 0.2 wavelengths (five elements per wavelength) to ensure sufficient resolution of the wave. The PMLs are swept along the absorbing direction. With the low degrees of freedom represented in the model, the simulation takes just a few seconds to compute.
The results plot provides the norm of the total electric field distribution around the sphere, which describes the sum of the background and scattered field and the far-field approximation of the scattered field. In addition, the polar plot gives the modeling specialist insight into the far-field pattern on a specific plane, while the 3D far-field radiation pattern offers a clearer intuition of the scattered field (Fig. 3, again). These plots are the results of the circularly polarized background field illumination on a conducting sphere.
3D Analysis of the 2D Axisymmetric Simulation
In the real world, the scattered field response of a 3D metallic sphere is studied using a linearly polarized plane wave. The linear polarization can be formed by adding both a right-handed and left-handed circular polarization.
The 2D axisymmetric model is solved at m = 1 with the background field of left-handed circular polarization. The solution for the negative azimuthal mode with the right-handed circular polarization is easily extracted from the already-solved left-handed circular polarization case based on the symmetrical properties of the model. The coordinate transformation from cylindrical to Cartesian coordinate is involved when visualizing the 2D results in the 3D space. By conducting the 2D analysis on one side and mirroring the solution to the other side, we can translate that information into a 3D solution at a fraction of the computational cost.
4. RCS is compared between a full 3D model and a 2D axisymmetric model.
The 1D plot of the RCS comparison shows a reasonable agreement between 3D and 2D axisymmetric models (Fig. 4). The small discrepancy is observed from the forward- and backward-scattering responses, especially around the rotating axis.
Figure 5 shows the visualization of the 2D axisymmetric results in 3D. The rotating arrows represent the circularly polarized background field illuminating the sphere. The deformed slice plot is the norm of the r-component of the background field. The surface plot of the sphere is the norm of the total electric field. The other arrow plot describes the superposition of two circular polarizations that are equivalent to a linearly polarized background field in 3D.
5. Here’s a 3D representation of a 2D axisymmetric model.
Concluding Remarks
Efficient modeling techniques are critical to modern-day design and simulation engineers in the RF and microwave industry, regardless of the numerical analysis method used. The goal of simulation is to describe real-world devices and objects as close as possible through mathematical formulation. The preferred method to reduce computational time is to remove unimportant parts of an object that have negligible effects on the simulation results.
When simulating and analyzing axisymmetric objects such as spheres, as well as conical or dish antennas, the 2D axisymmetric modeling approach offers orders of magnitude faster computation compared to a full 3D model. The scattering of a linearly polarized background field, as well as the far-field radiation pattern of antennas excited by the TE11 circular waveguide mode in 3D, can be extracted from the fast 2D axisymmetric simulations.
Addressing a simple shape, such as a sphere, may appear to be a quick and easy analysis until we realize the impact of the electrical size of the model in terms of wavelength. To maintain integrity in modeling an electrically large real-world component, simplifying the simulation process without losing accuracy is possible by taking advantage of 2D axisymmetric studies.
Jiyoun Munn is RF Technical Product Manager at COMSOL.
