Algorithms to Antenna: Simulating Wideband Behavior in Wireless Communications and Radar Systems
Increasing frequency bandwidth in a system yields a corresponding increase in the potential capacity of its channels. This helps enable higher data rates in communication systems and greater range resolutions for radar systems. The boost in bandwidth can also improve robustness to multipath fading for both of these types of systems.
Typically, wideband systems are designed to operate with a bandwidth of greater than 5% of their center carrier frequency. In contrast, narrowband systems operate with a bandwidth that’s typically 1% or less of the system's center frequency.
To illustrate this concept, Figure 1 shows plots from a radar system using both narrowband (top) and wideband (bottom) waveforms. Each plot illustrates the results of a matched filter operation on a set of returns. Three targets are in the radar field of view. Note that once the targets are located within the limits of the radar range resolution, it’s hard to see all three when using a narrowband waveform. With the wideband waveform, it’s easy to see all three targets even when they are just a few meters apart.
1. Shown are radar returns with narrowband and wideband waveforms.
For wideband systems, regardless of whether they are used in radar or communications systems, a large frequency range of operation can result in different responses across the frequency band. When modeling wideband systems, it’s important to account for the behavior of different frequencies to match what will happen in your actual system.
Some examples are included in the following sections to show where modeling wideband performance is important across some typical systems.
Channel Models
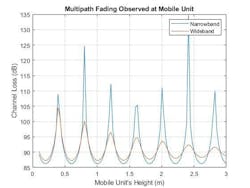
In a communications system, a narrowband channel can be very sensitive to multipath fading. If you think of a base station communicating with a mobile device, slight changes in the device’s height may result in considerable signal losses. The channel's fading characteristics can be plotted by varying the mobile unit's height across a span of operational heights for this wireless communication system.
The sensitivity of the channel loss to the mobile unit's height for the narrowband system is clear. Deep signal fades occur at heights that are likely to be occupied by the mobile users. Increasing the channel's bandwidth (in this case, to 10%) can improve the communication link's robustness to these multipath fades.
The received signal at the mobile unit for this wideband system’s various operational heights is shown in Figure 2.
2. Multipath fading is shown at narrowband and wideband frequencies.
As expected, the wideband channel provides much better performance across a wide range of heights for the mobile unit. In fact, as the height of the mobile device increases, the impact of multipath fading almost completely disappears. This is because the difference in propagation delay between the direct and bounce path signals is growing, reducing the amount of coherence between the two signals when received at the mobile device.
Antenna Design
Another example in which modeling wideband performance is important involves using an antenna element and the corresponding antenna array using that element. Consider the case of a blade dipole as a single antenna element and a two-×-two array built using this element.
Strip dipoles have an impedance with a capacitive component. These elements typically possess a narrow impedance bandwidth. Widening the dipole makes it easier to impedance match over a broader frequency range. These wide dipoles are known as blade dipoles.
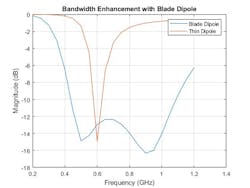
The blade dipole consists of two identical metallic arms that include a tapered section close to the feed. The tapered section ensures a better impedance match to 50 Ω. Figure 3 shows the physical structure of the element along with the magnitude versus frequency performance.
3. Blade dipole (top) and corresponding performance comparison to a thin dipole (bottom) are revealed.
Note the magnitude comparison between the thin dipole and blade dipole where the reflection coefficient curve crosses −10 dB. The blade dipole provides much greater performance across a wide bandwidth.
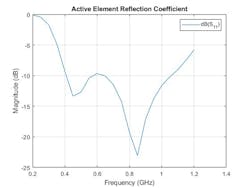
Figure 4 depicts the blade dipole in a two-×-two array. We also see broadband performance using the array. The bandwidth is approximately 2.6:1, measured as the ratio of the highest to the lowest frequency at which the reflection coefficient curve crosses −10 dB. This type of array can then be used as part of a larger system model to achieve a higher level of fidelity.
4. This is the magnitude response of a two-×-two array using a blade dipole.
Target Models
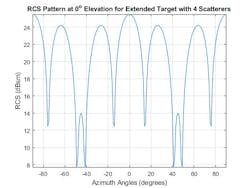
The next example relates to target modeling in a radar system. One way in which wideband systems improve detection performance is by filling in fades in a target's radar cross-section (RCS) pattern. This can be demonstrated by viewing an “extended” target built up from four cylindrical scatterers. Figure 5 shows the modeled narrowband RCS swept across various target aspect angles.
5. Shown are the scatterer structure (top) and RCS pattern for extended target (narrowband) (bottom).
We see that returns from the multiple cylinders in the extended target model coherently combine, which results in deep fades between 40 and 50 degrees. These fades may prevent the target from being detected by a radar.
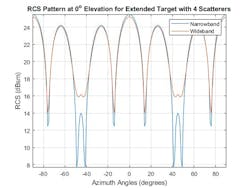
The RCS pattern for a wideband system operating at the same center frequency is shown as a comparison in Figure 6. Here, it’s assumed that the provided RCS model has been sampled at 1-MHz intervals on either side of the radar's center frequency.
6. RCS for narrowband and wideband target models are compared.
The contributions from the various scattering centers are modeled as before. Note that this approximation assumes that all of the target's scattering centers fall within the same range resolution bin.
The target's RCS pattern now has much shallower nulls between 40 and 50 degrees azimuth. The wideband waveform fills in these fades because, though a few frequencies may experience nulls for a given aspect, most of the bandwidth does not lie within the null at that azimuth angle.
Beamformers
The last example centers around beamforming. To validate the performance of a beamformer, let’s plot the response of an antenna element and an array of these elements. The array must maintain an acceptable array pattern throughout the bandwidth.
Figure 7 shows an element pattern that’s constant over the entire bandwidth. In this case, the bandwidth covers a range between 57 and 63 GHz.
7. This is an element pattern across a desired frequency range.
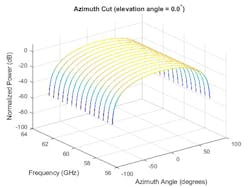
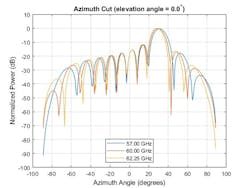
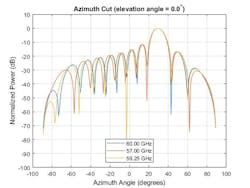
In Figures 8 and 9, one can see the response pattern of an antenna array plotted over the same set of frequencies. This plot shows that the pattern mainlobe decreases with frequency.
8. Azimuth cut of array pattern across a wideband frequency range.
9. The response pattern for a narrowband beamformer is given across multiple frequencies.
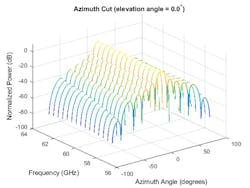
Now, a sub-band phase-shift beamformer is applied to the array with the same steering direction of 30 degrees azimuth and 0 degrees elevation. This beamformer is better suited for wideband signals. Figure 10 shows the response pattern of the array using the weights and center frequencies from the beamformer.
10. This is the response pattern for a wideband beamformer across frequencies.
The resulting response yields a main beam pattern that’s consistent across frequencies as desired.
Wideband systems introduce additional complexities over narrowband systems. Modeling these types of systems before they are built can help prevent surprises later in the development cycle. This post showed a few examples to help illustrate how wideband systems can be modeled.
To learn more about the topics covered in this blog, see the links below or email me at [email protected].
- Wideband Radar System Design (webinar): Learn to model and simulate wideband radar systems, explore alternative system architectures, and make system-level tradeoffs.
- Modeling a Wideband Monostatic Radar in a Multipath Environment (example): Learn how to simulate a wideband radar system.
- Wideband Blade Dipole Antenna and Array (example): This example shows the analysis of a blade dipole as a single element and in a two-×-two array with emphasis on its wideband behavior.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.
Honglei Chen
Principal Engineer
Honglei Chen is a principal engineer at MathWorks where he leads the development of phased-array system simulation. He received his Bachelor of Science from Beijing Institute of Technology and his MS and PhD, both in electrical engineering, from the University of Massachusetts Dartmouth.