Regenerate Coherent Carriers From PSK Signals
This file type includes high resolution graphics and schematics when applicable.
Designing coherent carrier-recovery circuitry for demodulating suppressed-carrier phase-shift-keying (PSK) signals involves several trade-offs and performance considerations. A number of approaches is available, although this article will focus on a design for a multimission PSK demodulator which can accommodate varying data rates in different PSK modulation schemes without requiring any change in configuration. Such a demodulator is ideal for satellite ground stations receiving data from various remote-sensing satellites of different payload characteristics.
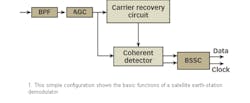
Figure 1 shows a simplified configuration for the PSK demodulator.
It consists of an input automatic-gain-control (AGC) amplifier, coherent carrier-recovery circuitry, and coherent detector circuitry. Intermediate-frequency (IF) signals plus noise are bandpass filtered, boosted through the AGC amplifier, and routed in parallel to the carrier-recovery circuit and the coherent data detector. The carrier-recovery circuit regenerates the coherent reference for demodulation that is routed to the data detector. The coherent data detector extracts in-phase (I) and quadrature (Q) data streams, which are lowpass, filtered and fed to the corresponding plug-in of the bit-synchronizer and signal-conditioner (BSSC) unit. The BSSC unit recovers the coherent symbol timing for synchronizing the data to the symbol timing clock. In this case, the BSSC unit supplies serial data and clock outputs.
Most applications can be satisfied by one of the three types of carrier-recovery configuration: a multiplication loop (such as a squaring loop for BPSK), a Costas loop, and a remodulator loop.1,2 Other types of carrier-recovery schemes are extensions or modifications of these techniques. For example, a multiplication loop for MPSK (Fig. 2) makes use of an Mth-order nonlinear square-law function preceded by a bandpass filter to remove the modulation.
A conventional PLL, operating at a frequency of M × fc, where M is the harmonic multiplier and fc is the carrier frequency, locks to the Mth-harmonic component of the nonlinear output while the voltage-controlled oscillator (VCO) is divided by M to provide the desired reference carrier frequency.
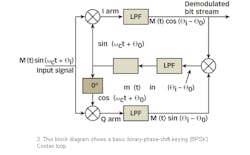
In a BPSK Costas loop (Fig. 3), an estimate of carrier phase is obtained by multiplying (with two phase detectors) the input suppressed carrier plus noise with the output of the VCO and a 90-deg.-shifted version of the VCO's signal, respectively, filtering the results of the two multiplications, and using the product of the two filtered signals to control the VCO's phase and frequency. When the filters in the I and Q arms are controlled by integrate-and-dump circuits, the loop is called a Costas loop with active arm filters.3-6
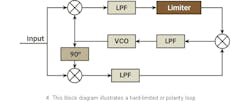
An optimal phase estimator requires a hyperbolic tangent b/N0)> nonlinearity following the I-arm filter. For large values, tanh(x) equals the polarity or sign of x(±1), and can be implemented with a hard limiter.7 An optimum loop has been practically realized by approximating this hyperbolic tangent nonlinearity.8 This type of loop is called the hard-limited or polarity loop (Fig. 4).
The inclusion of a limiter introduces a signal suppression factor that can improve or degrade the tracking performance.6 Also, the limiter allows the replacement of the analog third multiplier, which yields the loop error signal, with a chopper-type device that typically exhibits much less DC offset or DC drift instability.9
In a hard-limited modified Costas loop, a quadrature arm filter is removed to improve the acquisition characteristics.10 The modified Costas loop generates a frequency-restoration force approximately proportional to the frequency error at the output of the third multiplier. During acquisition, the loop acts like an automatic-frequency-control (AFC) circuit with a bandwidth proportional to the square of the Costas loop bandwidth. This modification allows acquisition for frequency offsets greater than the loop bandwidth. Pull-in is achieved from initial frequency errors compatible to the cutoff of the lowpass filter in the I channel. Unfortunately, a trade-off is degradation in the loop tracking jitter.6
The hard-limited modified Costas loop achieves significant improvement in false-lock performance, at the cost of increased tracking jitter.11 The false-lock phenomenon arises in Costas loops while acquiring suppressed carrier signals (rather than unmodulated carriers), due to the distortion created by the finite bandwidths of the I and Q filters. In essence, the incoming data pulses in the I and Q channels are no longer ideally rectangular and, when combined, may produce a DC control term when the received signal is offset from the VCO by an integral multiple of one-half the data rate (data-related sidebands).12,13
The false-lock state corresponds to the condition whereby a stable null point exists in the loop's error characteristic as a function of phase (the so called "S-curve" of the loop) when the receiver's local VCO is offset in frequency from that of the received signal in noise.11 Another modified Costas loop configuration, where the sum of the squares of the I and Q channels is processed to contribute to the loop error signal, may inhibit stable operating points at false lock.13
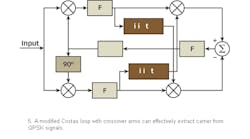
A conventional quadrature Costas loop has been used for the carrier extraction of QPSK signals.9 However, the most popular approach uses a modified Costas loop with loop crossover arms (Fig. 5).14,15
The sign of the output of the arm filters produced by the limiter is used to crossover and mix with the signal from the opposite arm. The limiters effectively demodulate the QPSK quadrature bits and the crossover produces a common phase-error term that is cancelled after subtraction. The subtraction leaves a remainder error term that is used to generate an error signal for phase control of the loop VCO, thereby closing the loop.
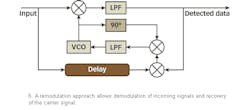
Remodulation is another popular carrier-recovery technique (Fig. 6).
The incoming signal is demodulated and the message waveform is recovered. This baseband waveform is used to remodulate the incoming signal; if the waveforms are rectangular and time aligned, the remodulation procedure removes the modulation completely. The output of the balanced modulator has a pure carrier component at the input frequency and the PLL tracks the component. The remodulator is stochastically equivalent to the polarity loop, i.e., the hard-limited Costas loop.16 The remodulator, however, is typically implemented at low frequencies (below IF) and cannot be used for multiple data rates due to time delays which impact the realization of a wide-band synchronizer.17
Page Title
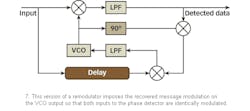
Another version of the remodulator loop imposes the recovered message modulation on the VCO output so that both inputs to the phase detector are identically modulated (Fig. 7).
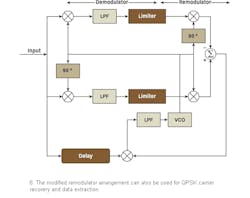
The low-frequency product of two such waveforms results in a DC component of the same amplitude as if the inputs had no modulation.18 This version of the remodulation technique can also be applied for QPSK carrier recovery and data extraction (Fig. 8).9
Although stochastically equivalent, the QPSK remodulator loop has been shown to exhibit a somewhat faster acquisition time when compared to a conventional QPSK Costas loop.16
Carrier recovery from Unbalanced QPSK (UQPSK) signals (wherein the powers as well as data rates of the quadrature directions are unequal) can also be performed with the same conventional techniques described above; though the tracking performance in the presence of noise and interference must be analyzed differently. If all of the power is concentrated in one quadrature direction (standard suppressed carrier PSK), a squaring loop will be adequate to track the signal. On the other hand, if equal amounts of power are allocated to each of the quadrature direction, then a squaring loop can not track this signal and a fourth (or higher) order loop must be utilized. Reference 19 offers suggestions as to which of the two tracking loop configurations should be used for intermediate values of power apportionment. If the signal is much larger than the thermal noise (which is generally the case in high data rate systems) a squaring loop (or equivalently a Costas loop) should be used provided the high power phase contains more than 73 percent of the total power. References 20-22 offer even further detail on the analysis of these carrier-recovery techniques, while refs. 23 and 24 detail additional carrier-recovery approaches not covered here.
Remote-sensing satellites transmit high-data-rate digitally modulated signals pertaining to the satellite sensor information. Different satellites transmit different data rates in different suppressed-carrier modulation schemes including QPSK/BPSK/UQPSK. It is a simple matter to design the ground stations for receiving these signals with the feed and front-end system broad enough to accommodate the reception of signals anywhere in the assigned spectrum. A separate data-rate-specific demodulator and bit-synchronizer, however, must be used for each satellite payload if a mission-specific design approach is used. This increases the system complexity as well as the cost. A demodulator with multi-mission capabilities, therefore, provides a low cost solution to the problem of receiving multiple high-data-rate signals at different data rates in QPSK/UQPSK/BPSK schemes.25
Various techniques can be used to recover the carrier from BPSK, QPSK, or UQPSK signals with appropriate selection of the loop configuration. However, not all the configurations can be used to receive multiple data rates without requiring any change in the loop configuration/parameters. For example, the remodulation loop can receive only one data rate due to the requirement of the time-alignment between the incoming modulated signal and the demodulated baseband signal before the multiplication of these two signals to remove the modulation.17 The delay introduced by the delay line used to obtain this time-alignment must be changed appropriately each time a different data rate, other than the one for which the delay is set, is to be received. Thus, a remodulation loop cannot be used in a multi-mission, multi-data-rate ground station.
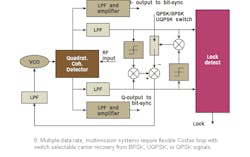
Based on these special requirements of a multi-mission remote-sensing satellite ground station, the following are used for realizing the coherent carrier-recovery process in a multi-mission demodulator: a fourth-order Costas loop that can be switched to a second-order configuration; a multiplication loop that can be switched between fourth-order and squaring functions; and a long PLL carrier-recovery loop.25,26 Figure 9 depicts the Costas loop configuration wherein the input modulated signal (from the AGC amplifier) is split into two paths and mixed with the quadrature LO signal (from the PLL's VCO) to produce the desired I and Q baseband signals.
These signals are amplified in broadband DC-coupled amplifiers and passed to the bit synchronizer for further processing. The samples of the same I and Q data streams are also amplified and filtered in the Costas-arm filters. The arm-filter outputs are fed to the Costas phase detectors, which generate a phase-error estimate through a hard-limited polarity loop. The loop has two operating modes: one as a carrier reference loop for BPSK (or UQPSK) and the other for QPSK carrier regeneration. When BPSK mode is selected, the loop provides second-order nonlinearity characteristics. When QPSK mode is selected, it provides fourth-order nonlinearity characteristics. The corresponding output phase-error estimate is fed to the integrator of a PLL. The integrator output drives the VCO. The VCO's output is fed through a quadrature hybrid to create the LO signals for the I and Q mixers.
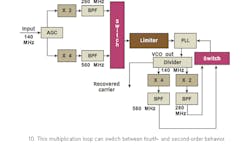
Figure 10 shows a multiplication loop that can switch between second-order behavior for UQPSK/BPSK carrier recovery and fourth-order behavior for QPSK carrier recovery.25,26 The one-sided lowpass arm filters of Fig. 9 are replaced here by the double-sided bandpass filter centered at the (M)IF carrier frequency. The double-sided noise bandwidth of this prefilter is selected for a midrange symbol rate. The noise bandwidth of the prefilter for the second-order loop is chosen for the I-channel data rate of the UQPSK signal. Selection is done between the second-order and fourth-order output into the PLL carrier reference. The VCO output is also simultaneously selected for either ×2 or ×4 multiplication. The VCO output is sent to a power divider and one divider output is taken as the coherent carrier reference.
The Costas and multiplication loop carrier-recovery approaches mentioned earlier suffer from several limitations for handling multiple data rates encountered in a remote-sensing satellite ground station. Wideband pre-filtering prior to the nonlinearity for modulation wipe off has to be done in any carrier-recovery configuration to accommodate the highest data rate modulated signals for minimizing the squaring loss. The excess noise bandwidth in the filter, while receiving the lower data rate modulated signals, however, increases the squaring loss and consequently reduces the output signal to noise ratio severely. The acquisition threshold of the carrier referencing loop vis-à-vis the input C/N ratio increases resulting in reduction in the link margin while receiving the lower data rate modulated signals.
Page Title
It is possible to use a narrow bandpass filter to improve the signal-to-noise ratio at the input of the PLL. However, the pre-PLL bandwidth control is decided by the maximum Doppler offset on the received signal. For some low circular satellite orbits, this may be as high as ±400 kHz. As a result, the pre PLL filter passband response must be flat at least over ±2 MHz resulting in a noise bandwidth much larger than that. The carrier referencing in the above design configurations for a multidata-rate reception system, hence, faces several constraints and uncertainties in exact estimation.
Since there is no solution to these problems in the two carrier-recovery techniques (multiplication and Costas loop methods) for a remote-sensing satellite ground station, a scheme was designed at the National Remote Sensing Agency (Hyderabad, India) by the authors and their colleagues. The scheme incorporates a wider prefilter at the input of the carrier-recovery nonlinearity but also facilitates optimization of the SNR at the input of the carrier referencing PLL by using a narrow bandpass filter.26-30 The scheme provides better lock threshold performance and improved stability with low loop jitter in regenerating the coherent carrier for low input signal-to-noise ratios at different modulation schemes (BPSK, UQPSK, and QPSK) and input data rates.
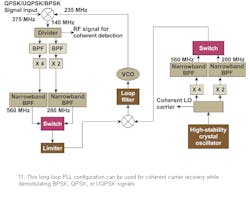
The long-loop PLL configuration was used for coherent carrier recovery in a demodulator (Fig. 11).26
Incoming BPSK, QPSK, or UQPSK signals, at 375 MHz, were mixed with the VCO signal from the carrier referencing PLL to provide an IF signal. The IF signal was passed through a three-way power divider. One output from the divider goes to the coherent detector for I and Q detection while the other two outputs are fed to the corresponding bandpass filters with bandwidths selected optimally for minimum squaring loss for the highest baud rate in each of the QPSK/UQPSK (BPSK) formats.
The filtered signal is then multiplied (through the nonlinearity) to remove the modulation. The ×2 nonlinearity is used for UQPSK signals (in the same processing chain for BPSK) while the ×4 nonlinearity is used for QPSK. The fourth- or second-harmonic component of the IF carrier frequency generated as the result of nonlinear operation is filtered through the corresponding narrowest-possible bandpass filter. The signal at the input of the narrowband bandpass filter always remains centered at a fixed frequency. The output from the narrowband bandpass filter is then phase locked with the 34 or 32 multiplied component of a stable crystal oscillator. The crystal-oscillator frequency is centered at the IF carrier frequency and becomes the coherent carrier reference for data detection after phase locking. The source frequency after multiplication is passed through a bandpass filter with identical characteristics as the one that is in the signal path at the input of the PLL. This ensures the correct phase referencing in the PLL. The PLL tracks the Doppler frequency variations of the input signal by correcting the VCO output frequency accordingly, while maintaining the IF output of the mixer at a constant frequency. The mixer output is power divided, with one portion fed to the coherent detector for data demodulation and the other to the loop. The VCO is swept for initial signal acquisition and is designed for acquiring the signal with a Doppler shift as high as ±500 KHz. As the Doppler effect is compensated prior to the carrier-recovery nonlinearity, the bandwidth control by using a narrow bandpass filter at the input of the carrier referencing PLL, hence becomes possible in this configuration and the S/N at the input of the PLL is maximized to improve the overall lock acquisition threshold of the PLL.
However, care must be taken to ensure that this narrowband bandpass filter is large enough with respect to the loop filter; otherwise, the transfer function of its equivalent lowpass filter will disturb the loop response. In addition, even if this filter is relatively large, its presence can considerably modify the loop operation during acquisition, causing, what is known as a false acquisition. This phenomenon is particularly prevalent when the number of poles is fairly high.31
The technique has provided an improvement of about 3 dB in QPSK and about 6 dB in BPSK mode in the acquisition threshold of carrier referencing PLL over conventional short loop configuration (PLL without pre PLL narrowband filter) for various data rates.26,28
Various design and configuration options have been outlined for the carrier recovery from PSK modulated signals. Not all options are suitable for receiving multiple data rates without requiring changes in the configuration design and circuit parameters. Only the hard-limited Costas loop and the multiplication loop can be configured effectively to receive signals from multiple satellites. However, with fixed I and Q filters, these configurations can accommodate at best a limited range of data rates, typically 40 to 110 Mb/s, due to the effect of squaring and self-noise components from nonlinearities and filtering operations.25 Fortunately, a unique carrier-recovery technique using a long-loop PLL configuration is suitable for receiving data from multiple satellites with different payload characteristics.
ACKNOWLEDGMENTS
The authors wish to express deep gratitude to Dr. K.N. Shankara, Director of the Space Applications Centre, Ahmedabad; Shri A.R. Dasgupta, Deputy Director of SITAA; Shri K. Bandyopadhyay, Group Director of SGSTG/SITAA; and Shri S.S. Valdiya, Head of SEID/SGSTG of SAC, Ahmedabad for their kind encouragement.
REFERENCES
- L.E. Franks, "Carrier and Bit Synchronization in Data Communication—A Tutorial Review," IEEE Transactions on Communications, Vol. COM-28, No. 8, pp. 1107-1120, August 1980.
- J.P. Costas, "Synchronous Communications," Proceedings of the IRE, Vol. 44, pp. 1713-1718, December 1956.
- M.K. Simon and W.C. Lindsey, "Optimum Performance of Suppressed Carrier Receivers with Costas Loop Tracking," IEEE Transactions on Communications, Vol. COM-25, No. 2, pp. 215-227, February 1977.
- W.C. Lindsey, Synchronous Systems in Communication and Control, Prentice-Hall, Englewood Cliffs, NJ, 1972.
- W.C. Lindsey and M.K. Simon, Telecommunication Systems Engineering, Prentice-Hall, Englewood Cliffs, NJ, 1973.
- M.K. Simon, "Tracking Performance of Costas Loops with Hard-Limited In-Phase Channel," IEEE Transactions on Communications, Vol. COM-2.6, No. 4, pp. 420-432, April 1978.
- S. Ritter, "An Optimum Phase Reference Detector for Fully Modulated Phase Shift Keyed Signals," IEEE Transactions on Aerospace and Electronic Systems, Vol. AES-5, No. 4, pp. 627-631, July 1969.
- A.G. Melo and H.J.A. da Silva, "Improved Performance QPSK Demodulator for Digital Satellite Radio," 1997 IEEE International Conference on Communications, Vol. 1 of 3, 8-12, Montreal, Canada, pp. 159-163, 1997.
- J. Mark Steber, "PSK Demodulation Techniques Provide Lowest Probability of Error," Microwave Systems News, pp. 150-176, June 1984.
- Charles R. Cahn, "Improving Frequency Acquisition of a Costas Loop," IEEE Transactions on Communications, Vol. COM-25, No. 12, pp. 1453-1459, December 1977.
- M.K. Simon, "The False-Lock Performance of Costas Loops with Hard-Limited In-Phase Channel," IEEE Transactions on Communications, Vol. COM-26, No. 1, pp. 23-34, January 1978.
- G.L. Hedin, J.K. Holmes, W.C. Lindsey, and K.T. Woo, "Theory of False Lock in Costas Loops," IEEE Transactions on Communications, Vol. COM-26, No. 1, pp. 1-12, January 1978.
- A.H. Makarios and T.C. Tozer, "False-Lock Performance Improvement in Costas Loops," IEEE Transactions on Communications, Vol. COM-30, No. 10, pp. 2285-2288, October 1982.
- R.M. Gagliardi, Introduction to Communications Engineering, Wiley, New York, 1978.
- J.K. Holmes, Coherent Spread Spectrum Systems, Wiley, New York, 1981.
- C.L. Weber, "Demod-Remod Coherent Tracking Receiver for QPSK and SQPSK," IEEE Transactions on Communications, Vol. COM-28, No. 12, pp. 1945-1953, December 1980.
- H. Yamamoto, K. Hirade, and Y. Watanabe, "Carrier Synchronizer for Coherent Detection of High-Speed Four-Phase-Shift-Keyed Signals," IEEE Transactions on Communications, Vol. COM-20, No. 4, pp. 803-807, August 1972.
- F.M. Gardner, Phase Lock Techniques, 2nd edition, Wiley, New York, 1979.
- J.S. Lesh, "Costas Loop Tracking of Unbalanced QPSK Signals," Proceedings of IEEE 1978 International Conference on Communications ICC 77, Vol. 1 of Three Volumes, Toronto, Canada pp. 16.2.1-16.2.5, June 4-7, 1978.
- M.K. Simon, "Two-Channel Costas Loop Tracking Performance for UQPSK Signals with Arbitrary Data Formats," IEEE Transactions on Communications, Vol. COM-29, No. 9, pp. 1275-1289, September 1981.
- W.R. Braun and W.C. Lindsey, "Carrier Synchronization Techniques for Unbalanced QPSK Signals—Part I," IEEE Transactions on Communications, Vol. COM-26, No. 9, pp. 1325-1333, September 1978.
- W.R. Braun and W.C. Lindsey, "Carrier Synchronization Techniques for Unbalanced QPSK Signals—Part II," IEEE Transactions on Communications, Vol. COM-26, No. 9, pp. 1334-1341, September 1978.
- A.N. D' Andrea and F. Russo, "Noise Analysis of a PSK Carrier Recovery DPLL," IEEE Transactions on Communications, Vol. COM-31, No. 2, pp. 190-199, February 1983.
- P.Y. Kam, "Maximum Likelihood Carrier Phase Recovery for Linear Suppressed-Carrier Digital Data Modulations," IEEE Transactions on Communications, Vol. COM-34, No. 6, pp. 522-527, June 1986.
- P.M. Rao, G. Umadevi, and P.K. Jain, "Design of Multifunction Digital Data Demodulator and Bit Synchronizer For Remote Sensing Satellite Data Reception," IETE Technical Review, Vol. 13, Nos. 4 and 5, pp. 233-240, July-Oct, 1996.
- P.K. Jain, Surendra Pal, and V.M. Pandharipande, "Analysis and Implementation of Carrier Recovery Process in a Multimission Remote Sensing Satellite Ground Station," RF Design, pp. 52-64, July 2003.
- P.K. Jain, Surendra Pal, and V.M. Pandharipande, "Real-time Quality Analysis of Digital Remote Sensing Satellite Signals," RF Design, pp. 14-20, March 2003.
- P.M. Rao, P.K. Jain, and C.S. Padmavathi, "Coherent Carrier Regeneration Using a Long Loop PLL Technique," Applied Microwave & Wireless, pp. 28-42, May 1998.
- P.K. Jain, Surendra Pal, and V.M. Pandharipande, "Continuous Measurement and Monitoring of Eb/N0 Ratio Received during a Remote Sensing Satellite-Pass at a Multi-Mission Ground Station," Proceedings of IEEE TENCON-2003 Conference, Vol. 4, pp. 1429-1434, Bangalore, India, October 14-17, 2003.
- P.K. Jain, Surendra Pal, and V.M. Pandharipande, "Performance Analysis of Long Loop PLL in Real Time Measurement of Received Eb/N0 and Carrier Recovery from PSK Modulated Signals of Remote Sensing Satellite," IETE Tech. Review, Vol. 20, No. 5, pp. 407-414, September-October 2003.
- A. Blanchard, Phase-Locked Loops—Application to Coherent Receiver Design, Wiley, New York, 1976.
This file type includes high resolution graphics and schematics when applicable.