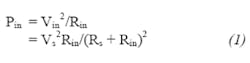High-speed components such as opamps and analog- to-digital converters (ADCs) are now typically available at RF and microwave frequencies for use in 50-Ohm systems. But since they are often at different impedances, parameters such as power gain and noise figure can be misused during a circuit analysis. To better understand the integration of baseband components into high-frequency circuits and systems, it may be helpful to review the concepts of voltage power gain as they apply to two-port networks, and then apply these concepts, along with additive noise models, to show how noise performance can be computed when there is no consistent system impedance.
Consider a general case where there is no consistent system impedance. The power source might be a high-impedance source, the amplifier could be an operational amplifier configured for a finite voltage gain, and the load could be an arbitrary resistance. A modest amount of circuit analysis will reveal the voltage and power gain of the amplifier with specific source and load resistances.
This set of three basic elements can be analyzed by using the method of Thevenin (or Norton) equivalents. The power source can be represented by a simple equivalent circuit (Fig. 1). The amplifier can similarly be modeled by a set of Z parameters as shown in Fig. 1. Assume the amplifier is unilateral. The parameters of this network are the input and output resistances and the Thevenin voltage gain a.
To compute the power gain from source to load, first compute the power absorbed by the input of the amplifier:
Compute the power absorbed by the load by means of
The power gain is then shown by Eq. 2:
To compute the voltage gain, first compute the input voltage, Vin. The input impedance of the amplifier is equal to Rin, so voltage Vin is:
Now compute the voltage at the output of the amplifier:
The voltage gain is then given by Eq. 3:
Usually the amplifier is specified in terms of its available power gain GA, which is defined with the source and load impedances equal to the input and output resistances, Rin and Rout, respectively. Equation 2 can be used to give the Thevenin voltage gain in terms of the available power gain GA. Set the source resistance, Rs equal to Rin, and the load resistance, RL, equal to Rout, and solve for parameter a:
Using this substitution, the power gain and voltage gain can be expressed in terms of GA:
If the input, output, and load resistances are all equal, the insertion power gain reduces to the available power gain. The voltage gain becomes the square root of the available power gain.
It is also useful to know Vs in terms of PAVS. For this purpose, Eq. 1 can be used, with the assumption that the load impedance is equal to Rs:
When the source, load, and port impedances of the cascade are all the same real value (Ro), the traditional power-based method of cascading elements can be used.
This method almost always uses the decibel (dB) as a unit of measure. In the most general terms, the decibel is defined as the logarithm of a ratio. A parameter such as power gain is a ratio, so it can be converted to dB as follows:
A parameter such as power is not a ratio, but it can be expressed in terms of its relation to a reference power level; typically 1 mW is used as the reference level:
Continue to page 2
Page Title
The decibel is fundamentally useful because it makes it possible to add quantities such as gain, power, and noise figure, rather than multiply them. Indeed, the assumption of a fixed system impedance and use of the decibel allows us to simply "snap together" the cascaded elements and compute gains, power levels, and noise figure. To compute the output power to the load, multiply the source power by the two-port power gain:
This can also be done by adding decibel units:
Consider the example shown in Fig. 2. The power available from the source is 5 mW, which is +7 dBm. Using Eq. 8, the load power is +21 dBm. The value of Ro is irrelevant; it is only important that the system impedances be some consistent value.
This method of computing the voltage and power gains of cascaded networks begins to fall apart, however, when the impedances at the interfaces between the source, networks, and load vary from Ro. Typically, an RF engineer will account for this by including the effect of impedance mismatch or voltage standing wave ratio (VSWR) in the cascade analysis. The idea of impedance mismatch deals with how the signal power is transferred from source to load at each interface. When the load impedance is not the complex conjugate of the source impedance, the power absorbed by the load is less than the power available from the source. It is possible to account for these power transfer losses and compute the overall power gain from the source to the ultimate load in this manner. But now the networks no longer simply "snap together" to yield the overall result.
To illustrate this, revisit the example from Fig. 2 with different values for the port impedances as shown in Fig. 3.
The source power and amplifier power gain have not changed. The actual power gain from the source to the load is, however, far from 14 dB. To compute the true power absorbed by the load, start with the specific circuit model parameters. From Eq. 7, PAVS = 5 mW, Rs = 50 Ohms, Vs = 1 VRMS, GA = 14 dB = 5 V/V, Rin = 100 Ohms, Rout = 200 Ohms, and from Eq. 4, a = 10.58 V/V and RL = 1000 Ohms.
Equation 2 can be used to compute the power gain, with Gp = 7.77 mW/ mW = 8.9 dB. This result is very different from the 14 dB result obtained by adding the source power to the amplifier gain in dB. This is because the port impedances are not fixed at some value Ro. The power available from the source is different from the actual power delivered to the amplifier. The available power gain of the amplifier is greater than the actual power gain into the load. This is often the case with elements such as operational amplifiers, which are well defined in terms of their voltage gain. Their input impedances are often far from 50 Ohms, and their outputs are usually low-impedance voltage sources.
The noise characteristics can also be modeled by Thevenin equivalents and Z parameters; see Fig. 4. The source model is simply the equivalent noise voltage, es, of the source resistance in series with a noiseless resistance Rs. To find the equivalent noise voltage, start with the noise power of this source. The noise power is defined as the power that the source resistance would deliver to a matched load:
The noise power ns is the thermal noise of the source resistance. This is equal to kT, where k is Boltzman's constant and T is the source temperature in degrees Kelvin. This substitution can be used to find es in terms of Rs:
Note the actual noise power delivered to the input of the network is not the same as ns if the source resistance is not matched to the input resistance:
Inside the two-port network, the noise voltage ea represents the noise added by the network. If the noise figure of the network is known, it is possible to compute the value of ea. This value will be determined from the noise figure later in this section. To find the total noise power delivered to the load, first combine es and ea at the input of the two-port model. These noise signals are uncorrelated, so they add on an RMS basis:
This noise voltage can now be referred to the Vin node of the two-port network:
The noise voltage that appears at the output terminals of the network is then:
From the noise voltage, it is possible to determine the noise power delivered to the load:
Many amplifiers, however, are specified for noise characteristics in terms of noise figure rather than input noise voltage. Noise figure can be specified with the source impedance set equal to Rin (Fig. 5). Noise figure is defined as the input signal to noise ratio (SNR) divided by the output signal to noise ratio under this set of conditions shown in Fig. 5. The input SNR can be computed as follows:
The output SNR is computed by:
The noise figure is then given by Eq. 13
Continue to page 3
Page Title
Parameter ea can be expressed in terms of noise figure by:
When the source resistance does not equal the input resistance, the effective noise figure will change. In general, then, the effective noise figure is equal to:
Here again, when the source, load, and port impedances of the cascade are all the same real value (Ro), much simpler formulas can be used to cascade elements. If the source noise power is kT, then the following apply:
An example appears in Fig. 6 where the source noise power is 3.98 x 10-21 W/Hz, or -174 dBm/Hz. The power gain of the amplifier is 14 dB and its noise figure is 6 dB. The noise power delivered to the load is, according to Eq 16, equal to -154 dBm/Hz.
Here again, if the network impedances vary from Ro, this method will yield inaccurate results. Refer to Fig. 7, which shows the same example with different values for the port impedances. The source power and amplifier power gain have not changed. The actual noise power delivered to the load is, however, far from -154 dBm/Hz. To compute the true power absorbed by the load, start with the specific circuit model parameters. From Eq. 9, ns = 4.14 x 10-21 W/Hz, Rs = 50 Ohms, es = 0.89 nV√Hz,GA = 14 dB = 5 V/V, Rin = 100 Ohms, Rout = 200 Ohms, and a = 10.58 V/V. From Eq. 4, F = 6 dB = 3.98 mW/mW. From Eq. 14, ea = 2.23 nV/ Hz and RL = 1000 Ohms. Equation 12 can be used to compute the noise power at the load, by Nout = 1.99 x 10-19 W/Hz = -157.0 dBm/Hz.
This is less than one-half the noise power obtained by using Eq. 16. The reason is that the terminal resistances are no longer all equal to one another. Put another way, the effective noise figure of the amplifier is not 6 dB but, from Eq. 15, Feff = 7.33 mW/mW = 8.65 dB.
Note that the noise power delivered to the load can be accurately computed using the effective power gain and noise figure. To do this, first compute the noise power delivered to the network input from Eq. 10, Nin = 3.52 x 10-21 W/Hz = -174.5 dBm/Hz. Add to this the effective power gain plus the effective noise figure, Nout = -174.5 dBm/Hz + 8.9 dB + 8.65 dB = -157.0 dBm/Hz. The method of adding decibels is now valid because the effective power gain and noise figure are used. The effective values are different than the values specified in a 50-Ohm measurement system.
If the port impedances are all the same, 50 Ohms for example, then the "snap together" RF approach is a quick and accurate way of computing voltage, power, and noise throughout the signal chain. In the case of the example shown in Fig. 3, however, this is not true. Although the available power gain of the amplifier is 14 dB, the actual power gain is only 8.9 dB. This is a large error because the port impedances are far from 50 Ohms. Similarly, Fig. 7 shows an example of an amplifier with a nominal noise figure of 6 dB. The effective noise figure of this amplifier with the source and load resistances shown is actually 8.65 dB. Again, the nonstandard port impedances make for a nontrivial calculation of the noise behavior.
Traditional RF methods for computing voltage, power, and noise work well for cascaded 50-Ohm amplifiers and filters. But when it comes to high-speed opamps and ADCs, for example, these methods produce results that are inaccurate. In such cases, a true two-port analysis technique such as the one suggested herein must be used.
Although most high-frequency circuits are based on a characteristic impedance of 50 Ohms, some systems, including cable-television (CATV) video networks, rely on matching components at some other impedance, such as 75 Ohms. Also, a growing trend in characterization and modeling of active devices involves measurements in non-5-Ohm environments. Because of changing source and load impedance conditions, it can be helpful to understand the behavior of an active device or component under different source and load impedances. Traditionally, high-speed, high-frequency components have been analyzed with a vector network analyzer and source and loadpull mechanical impedance tuners. But the emergence of active load-pull technology, where the impedance presented to a device under test (DUT) can be controlled electronically, allows for faster, more automated measurements under different impedance conditions. With improvements in mechanical impedance tuners from such suppliers as Maury Microwave and Focus Microwaves, and advances in active load-pull solutions from innovators like Mesuro Ltd., the options for characterizing baseband devices at non-50-Ohm impedances are no longer limited.