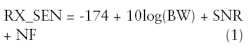Third-generation (3G) cellular networks offer unprecedented functionality and services for consumers, but also a host of challenges for handset designers. To provide the many services available, a mobile handset must work seamlessly across multiple wireless networks, such as wideband codedivision- multiple-access (WCDMA) and GSM/EDGE systems. Ideally, for reduced design cycle time and lower bill-of-material (BOM) costs, a practical transceiver solution should communicate across both networks as a WEDGE (WCDMA + EDGE) device. In the case of high-speed packetaccess capabilities, it would be considered a HEDGE solution.
In designing such a solution, it is important to understand the design specifications for each system and how they impact the transceiver's operation in terms of compatibility across the other systems In practical terms, even if a transceiver has been optimized for use with a particular wireless standard, such as GSM, it must also work with a relatively high performance level with other wireless standards, such as WCDMA.
When specifying multiple WEDGE chipsets, for example, appropriate trade offs can be made to select the best solution for a given application. For the radio-frequency-integratedcircuit (RFIC) design team, the chipset must meet the type approval tests listed in the WCDMA and GSM standards. Each test case in these type approval procedures corresponds to a particular specification in the design of the chipset.
The challenge in building a WEDGE receiver, for example, is because of the differences in requirements for WCDMA and GSM systems. In order to understand the performance requirements of a WEDGE receiver, it is necessary to carefully review the requirements of each wireless communications standard first to discover common ground. Once understood, the requirements of each standard can be readily translated into design specifications for the WEDGE receiver. A direct-conversion receiver will be used for the example analysis.
The requirements for a Global System for Mobile (GSM) Communications handset receiver cover a number of different equipment designations, including GPRS and EDGE. A GSM receiver typically covers four frequency bands at 850, 900, 1800, and 1900 MHz. A GSM receiver must be able to demodulate an input signal at a level of -102 dBm and achieve a bit-error rate (BER) of better than than 10-4. A GSM amplitude modulation (AM) suppression test requires a receiver sensitivity of -99 dBm with a -31-dBm Gaussian minimum-shiftkeying (GMSK) modulated blocker 6 MHz away. This test simulates the receiver operating in the desired channel and being jammed by the other inband channel. The worst-case signal blocker is a -23-dBm unmodulated tone 3 MHz away. This test evaluates the receiver's reciprocal mixing performance. Intermodulation tests are set up with two signals at -49 dBm. One is a single tone 800 kHz away from the carrier while the other is a GMSK-modulated signal 1600 kHz from the carrier. The co-channel interference is -9 dBc. The adjacentchannel interference is specified at +9 dBc while the alternate-channel interference is -41 dBc.
Based on these requirements, the following receiver specifications can be derived: noise figure, input second- order intercept point (IIP2), input third-order intercept point (IIP3), image-rejection ratio (IRR), adjacentchannel rejection, alternate-channel rejection, phase noise, input carrier compression point (ICP), automatic- gain-control (AGC) range, and analog-to-digital-converter (ADC) signal-to-noise ratio (SNR). In working through the list, the noise figure is determined first. For GSM, the channel bandwidth is 170 kHz. In the static case, the SNR requirement is 6 dB, plus a 3-dB fading margin. Thus, the minimal required SNR is 9 dB. The thermal noise floor is -174 dBm/Hz. The receiver (Rx) sensitivity (RX_SEN) can be found by Eq. 1.
The only unknown in this expression is the noise figure, which can be solved as 10.7 dB in the static case. This is the minimum acceptable noisefigure performance needed in a GSM system although, in reality, most GSM receiver chipsets have about a 7 to 8 dB margin.
The IIP2 is determined by means of an AM suppression test, using a receive signal of -99 dBm. Given a 9-dB SNR requirement, the noise floor due to AM interference must be at least -99 dBm - 9 dB = -108 dBm. Because IIP2 is determined with a single tone instead of the standard two-tone test, a 3-dB correction factor is added. The expression for IIP2 is shown in Eq. 2.
The IIP3 can be determined from the receiver's intermodulation requirements. The noise floor due to intermodulation is -108 dBm, just as in the case for IIP2. The expression for IIP3 is shown in Eq. 3.
The IRR can be calculated by determining the equivalent noise introduced by the image signal. With the signal sensitivity at -102 dBm and SNR of 9 dB, the total noise floor is essentially -111 dBm. The budget for IRR is selected so as to not cause a degradation of the noise floor by more than 0.1 dB. So, the total noise floor after image noise is added is -110.9 dBm. The total noise floor is the sum of the thermal noise floor and IRR noise floor. It can be expressed as in Eq. 4, with all terms converted from logarithmic form to linear form.
Using Eq. 4, the noise floor due to the IRR can be solved as -127.3 dBm. With a signal level of -102 dBm, the IRR is 25.3 dB.
Continue to page 2
Page Title
The GSM receiver's SNR is 9 dB, allowing it to easily tolerate co-channel interference of -9 dBc. Since the adjacent channel signal is +9 dBc, it will require the baseband channel select filter to have at least 18 dB rejection. Similarly, it will require at least 50 dB rejection for the alternative channel.
The worst-case blocker at 3 MHz offset dictates the local oscillator's (LO's) phase noise. Assume that the phase noise contributes 50 percent of the total receiver system noise. Thus, the noise floor due to the phase noise can be found from Eq. 5.
Since the blocker level is -23 dBm, the phase noise offset 3 MHz from the carrier must be -163.3 dBm (-23 dBm) = -140.3 dBc/Hz. The noise floor due to each source of interference is calculated first. Then the final specification can be calculated. This approach is fairly effective and has been used throughout this analysis.
The GSM receiver's ADC require ments depend on many factors. Assume that all blocker noises are well below the thermal noise floor. The remaining two major noise contributions are the thermal noise and the ADC noise. Using an approach similar to that for the IRR and assuming 0.01-dB SNR degradation from the ADC,2 the ADC implementation noise can be found from Eq. 6
This calculation of the GSM receiver's ADC implementation noise means that the ADC's noise floor must be 26.3 dB below the thermal noise floor. For a GSM system, the total required ADC SNR equals RX_SNR + ADC implementation_noise + fading margin. For a GSM system, the fading margin is 20 dB. The total ADC SNR required is thus 9 dB + 26.3 dB + 20 dB = 55.3 dB. Each ADC digital bit produces a 6-dB SNR. Therefore, a minimum bit resolution of 10 b is needed for the GSM receiver ADC. This result assumes that no AGC budget is required for the ADC and all other implementation noise sources are below the total noise floor.
The maximum input signal to a GSM receiver, which is specified as -15 dBm, sets the ICP and also sets the required AGC control range. The minimum specified signal level for a GSM receiver is -102 dBm. As a result, the minimum AGC range for the system is -15 dBm - (102 dBm) = 87 dB. By following this approach, the GSM receiver specifications have been derived and are shown in Table 1.1-3
A similar approach can be applied to finding the specifications for the WCDMA receiver,4-8 starting by stating the receiver's requirements as detailed in the wireless standard. In a WCDMA system, the receive band covers 2110 to 2170 MHz. The WCDMA standard requires a receive sensitivity of -117 dBm while meeting the BER requirement of 10-3. The inband modulated blocker is located 15 MHz from the carrier at a power level of -44 dBm. Since WCDMA is a frequency- division-duplex (FDD) system, the blocker from its own transmitter must be considered in this analysis. A WCDMA receiver intermodulation test uses one -46-dBm continuouswave (CW) blocker offset 10 MHz from the carrier of interest and one -46-dBm WCDMA blocker offset 20 MHz from the carrier. The blocker at the adjacent channel is -52 dBm over the full 3.84-MHz WCDMA information bandwidth. The worst-case blocker is a -46-dBm CW signal offset 10 MHz from the desired carrier.
The first step in the analysis is to calculate the WCDMA receiver's noise figure. The performance of a WCDMA receiver is improved by the technology's spreading property. The processing gain (PG) is 25 dB. The required ratio of the bit energy to the noise energy is Eb/I = 7 dB. The thermal noise floor is -174 dBm/Hz. The channel bandwidth is 3.84 MHz. The receiver sensitivity can be expressed by Eq. 7:
The only unknown in this case is the noise figure, which can be solved as 9.1 dB. Since only the thermal noise is being considered so far, the receiver must have a noise figure of no worse than 9.1 dB. As will be shown later, the noise figure specification must be tightened once other interferences are considered. The thermal noise, which depends on the PG and Eb/I, can be found from Eq. 8:
For a WCDMA system, a 3-dB correction factor must be subtracted from the noise floor.5 The IIP2 can then be calculated using Eq. 9:
For the IIP2 at the transmit band, the thermal noise floor is tightened up as 8 dB to accommodate the noise from the transmit band blocker. The calculated noise floor due to the AM blocker can be found to be equal to -105.1 dBm from Eq. 10.
Continue to page 3
Page Title
The -99 dBm in Eq. 10 is the total noise floor (the noise figure minus 108.2 dBm). It is the thermal noise floor within the WCDMA system's 3.84-MHz bandwidth. The noise figure is tightened to 8 dB. A 6-dB correction factor5 is needed to calculate the IIP2 due to transmitter leakage. Assuming a Class-III transmitter (+24 dBm), duplexer isolation of 50 dB, and duplexer insertion loss of 1.5 dB, the transmitter leakage can be assumed to be -24.5 dBm. With this assumption, the IIP2 can be calculated by means of Eq. 11:
Achieving an IIP2 of +50 dBm at the receiver input is a very challenging task. It puts tremendous pressure on the RF front end, especially the mixer. Techniques such as resistive load trimming or bias current trimming in a mixer design are possible solutions to intentionally introduce asymmetry to reduce mismatch.
To calculate the IIP3, the noise floor due to intermodulation must be calculated first. Assuming that the intermodulation is 15 percent (-8 dB) of the total noise budget, the noise floor can be found by means of Eq. 12 and the IIP3 by means of Eq. 13:
For a WCDMA system, the signal level is below the noise floor. The image-rejection specification is derived from the error vector magnitude (EVM) specification. It is typically specified as 25 dB.
The -52 dBm blocker at the adjacent channel sets the minimal adjacentchannel selectivity (ACS) requirement. The receiver is only required to meet a sensitivity level of -103 dBm for this test. With a PG of 25 dB and Eb/I of 7 dB for the WCDMA system, the noise floor due to the adjacent channel blocker can be found from Eq. 14:
The blocker in the adjacent channel must be filtered below the noise floor listed in Eq. 14. Thus, the ACS is -52 dBm - (-85 dBm) = 33 dB.
The ICP for a WCDMA receiver is set by the maximum in-band blocker signal level. It is reported to be -25 dBm.6 With a crest factor of 10 dB for a WCDMA signal, the ICP is set to be -15 dBm. With a minimum input signal of -117 dBm, the total required AGC range is 102 dB.
A blocker signal of -46 dBm at 10 MHz offset from the carrier sets the phase-noise specification for a WCDMA receiver just as in the GSM case. If the phase noise is assumed to be 5 percent (-13 dB) of the total noise budget, then the noise floor due to the phase noise is -99 dBm - 13 dB = -112 dBm. Since the channel bandwidth in a WCDMA system is 3.84 MHz, the phase noise for a WCDMA receiver can be calculated by Eq. 15:
The ADC requirements depend on the carrier-to-noise ratio (CNR), the fading margin, and the implementation noise margin.7,8 The CNR is set to be -7 dB.9 The fading margin is 4 dB for WCDMA. As in the GSM case, the ADC is assumed to degrade the noise floor by 0.01 dB. This requirement is based on the condition that the ADC noise floor must be 26.3 dB lower than the total noise floor of the system, as shown in Eq. 6. The ADC SNR requirement is calculated to be -7 dB + 4 dB + 26.3 dB = 23.3 dB. Thus, an ADC with minimum bit resolution of 4 b is required. This calculation is based on assumptions that all interference signals such as IIP2, IIP3, and phase noise are below the thermal noise floor and no AGC budget has been allocated. With this final calculation, the specifications for the WCDMA receiver are shown in Table 2.
Those results show a noise figure of 8 dB for effective WCDMA operation, with in-band IP3 if -17 dBm and input IP2 of +14 dBm offset 15 MHz from the carrier of interest. The required phase noise is found to be -131.84 dBc/Hz offset 10 MHz from the carrier, which implies a fairly lownoise synthesized signal source for WCDMA operation. The adjacentchannel selectivity (ACS) is based on the WCDMA receiver sensitivity level of -103 dBm as stated in the standard, and filtering the blocker in the adjacent channel to a level below the noise floor, resulting in an ACS of 33 dB.
This report has covered the analysis of both GSM and WCDMA receivers to show the specifications needed for a combined WCDMA and EDGE or WEDGE receiver. Before proceeding with any WEDGE receiver design, a more thorough analysis should be done with simulation software.
Continue to page 4
Page Title
REFERENCES
1. Tyson Tuttle, "Introduction to Wireless Rx Design," ISSCC 2002 Tutorial.
2. B. J. Minnis et al., "Non-complex signal processing in a low-IF Rx for GSM," IEE Proceedings of Circuits, Devices, and Systems, Vol. 149, No. 516, 2002.
3. Rahul Magoon et al., "A Single-Chip Quad-Band (850/900/1800/1900 MHz) Direct Conversion GSM/GPRS RF Transceiver with Integrated VCOs and Fractional-N Synthesizer," IEEE Journal of Solid-State Circuits, Vol. 37, No. 12, 2002.
4. O.K. Jensen et al., "RF Rx Requirements for 3G W-CDMA Mobile Equipment," Microwave Journal, February 2002.
5. Qiuting Huang et al., "A 1.5-V 45-mW Direct-Conversion WCDMA Rx IC in 0.13-m CMOS," IEEE Journal of Solid-State Circuits, Vol. 38, No. 12, Dec. 2003.
6. Andreas Springer et al., "RF System Concepts for Highly Integrated RFICs for W-CDMA Mobile Radio Terminals," IEEE Microwave Theory & Techniques, January 2002.
7. S. K. Reynolds et al., "A direct conversion Rx integrated circuit for WCDMA mobile systems," IBM Journal of Research & Development, Vol. 47, No. 2/3, March/May 2003.
8. Massimo Brandolini et al., "Toward Multistandard Mobile Terminals-Fully Integrated Rx Requirements and Architectures," IEEE Microwave Theory & Techniques, March 2005.
9. QiZheng Gu, RF System Design of Transceivers For Wireless Communications, Springer, New York, 2005.