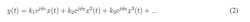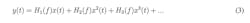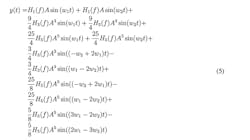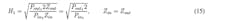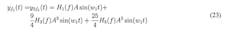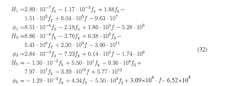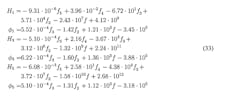Determining Volterra Kernels for Nonlinear RF Power Amplifiers
Download this article in PDF format.
The two methods presented in this article estimate first-, third-, and fifth-order Volterra kernels for an RF power amplifier (PA) using common RF laboratory instruments. In the first method, single measurement readings are employed to determine the kernels, while the second approach utilizes least-squares curve adaptation of measured data. Comparisons between the two methods discussed here and others described in existing publications reveal that these methods are easier to perform.
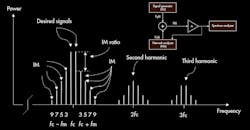
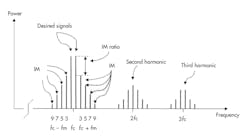
When an amplifier operates in the nonlinear region, it produces unwanted signals, namely harmonics. The second-, third-, and higher-order harmonics are outside of the amplifier’s bandwidth and can thus be filtered out. However, unwanted signals close to the fundamental (intermodulation products) cannot be filtered out and will interfere with amplified input signals and cause nonlinearity (Fig. 1). Furthermore, channel selectivity, detection efficiency, quality, and more importantly, spectral efficiency are impacted, leading to poor wireless-network capacity.1, 2
1. The distortion products in an RF power amplifier are shown.
To reduce the impact of nonlinear effects, a mathematical model is needed to describe and represent these unwanted signals.3 Overcoming these signals can be accomplished through various methods, such as feedback reduction.2
The Volterra series is a polynomial representation of nonlinear systems.4 Similar to the Taylor series, the Volterra series serves as a model for nonlinear behavior. In terms of problem solving, the most difficult and crucial aspect involves determining the coefficients of the power series. If the kernels of an amplifier are determined, the Volterra series can be applied for theoretical analysis and simulation of the amplifier.
The complexity associated with determining the Volterra series’ coefficients led to the lack of interest in this method. Although the Volterra series is a very good representation of broadband systems, few publications exist on this subject.5, 6, 7
There are different types of unwanted signals, such as harmonic and intermodulation (IM) products (Fig. 1, again). The second-, third-, and higher-order harmonic signals can simply be filtered out because they are far away in frequency from the desired signals. However, the IM signals (third-, fifth-, seventh-, and ninth-orders) are located near the desired signals, making it impossible to filter them out. As mentioned, this will lead to a lower system spectral efficiency.6
The main focus of this work is the broadband RF PA, which experiences frequency-dependent nonlinearity. Frequency-independent nonlinearity occurs in a narrowband RF PA.
Nonlinear systems, such as RF amplifiers, have two kinds of nonlinearities: the nonlinearity between the amplitudes of the input and output signals and the nonlinearity between the phases of the input and output signals. These two nonlinearities are divided into two categories: memory-less systems and systems with memory.2
The nonlinearity of the memory-less systems is frequency-independent. In other words, these systems do not have any inductors or capacitors. If we ignore the phase, the mathematical representation of these systems is:4
If we do not ignore the phase, the nonlinearity is represented by a complex power series:
where k1ejφ1, k2ejφ2,… are constants.
In systems with memory, the nonlinearity is frequency-dependent—for example, an RF amplifier. In these systems, nonlinearity is described by the Volterra kernel, which is also called a power series with memory.2, 4, 6
Suppose we have a system with two input signals of different frequencies (we will call them f1 and f2). By using the Volterra series equation, all of the terms that have H2(f), H4(f), H6(f)… are dropped because they are far away from the desired frequency. These terms are simply filtered out, and we have:
This experiment tries to estimate the Volterra kernels H1(f), H3(f), and H5(f) in a frequency band for an RF amplifier. The reason for not tracing higher-order kernels is that, practically speaking, it’s very hard to specify them.
Because the amplifier is band-limited and our interest lies in the IM signals around f1 and f2, we can ignore all other frequency bands except the frequency band around f1 and f2. Note that the band-limited amplifier is not specified for frequencies much larger than f1 and f2. Thus, Equation 4 can simplify to:
We can represent Equation 5 as follows:
where f3 = 2f1 – f2, f4 = 2f2 – f1, f5 = 3f1 – 2f2, f6 = 3f2 − 2f1
and:
where yf1 is part of y(t), which contains only the frequency f1. The expressions containing other frequencies can be obtained in a similar manner.
The Volterra kernels are complex numbers and can be represented in rectangular or exponential form. In this experiment, the exponential form has been chosen, which means six terms should be estimated: H1, φ1, H3, φ3, H5, and φ5.
Methods for Determining the Volterra Kernels
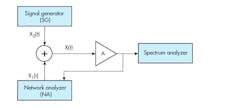
2. This is a principal sketch of the measurement setup.
Figure 2 shows the principle sketch of the circuit diagram used to perform measurements. The amplifier’s input signal is created by adding a signal from the network analyzer (NA), x1(t), and a signal from the signal generator (SG), x2(t). Hence:
which yields:
The input amplitude is:
Method 1
The purpose of this method is to determine points (Pin, Pout) on the input power curve as well as points (Pin, φout) on the phase curve for the frequency, f1. We can then apply these points to estimate kernels. The number of points is determined by the number of kernels that need to be estimated. First, look up a point that can be used to estimate H1(f). Then, look up another point that together with the estimated H1(f) can be applied to estimate H3(f), and so on.
3. Plotted is the output power as a function of the input power at f1. In Area 1, the first-degree nonlinearity dominates. In Area 2, the first- and third-degree nonlinearities dominate. Lastly, the first-, third-, and fifth-degree nonlinearities dominate in Area 3.
First, for the point (Pin1, Pout1) in the graph of Figure 3 in which the amplifier is linear, we estimate H1(f).
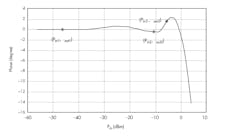
We determine φout1 in Figure 4 via point Pin1.
4. Shown is the angle of the frequency f1 as a function of the input power.
This yields:
and
where A = √Pin1Zin gives the following equation for H1:
Now, for the second points (Pin2, Pout2) and Fout2 in Figures 3 and 4 in which the first- and third-degree nonlinearity dominate, we estimate H2(f).
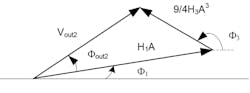
5. This vector analysis describes Equation 17.
By using the vector analysis as shown in Figure 5, we obtain:
Since Vout2, φout2, H1, φ1, and A are known, we calculate H3 and φ3 with the following equations:
Finally, H3 is estimated as:
By the same approach, for the third points (Pin3, Pout3) and φout3 in the curves in Figures 3 and 4, where the first-, third-, and fifth-degree nonlinearity dominate, we estimate H5(f).
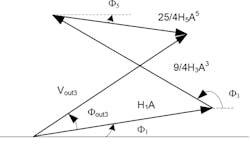
6. Equation 23 is represented by this vector analysis.
Using the vector analysis in Figure 6, we obtain:
where:
Finally, the estimated H5 is:
Method 2
In this method, the data from frequency f1 is used. The method is based on the polynomial adaptation. To this end, we shall try to approximate the values Pout(Pin) and φout(Pin), which is known by the data measurements via the following equation:
where:
and:
Here, the least-squares method for the polynomial adaptation is used. Hence:
This polynomial adaptation yields the values of y1, y3, and y5 in Equation 28. From these values, the kernels, namely H1(f), H3(f), and H5(f), can be easily calculated.4 To determine the accuracy of this approximation, we can substitute the obtained kernel values in Equation 28 and then vary the input amplitude A and calculate yf1 for all values of A. This method is easier to implement than the first method and allows for the possibility of estimating higher grades of the Volterra kernels.
In these two methods, the Volterra kernels have been estimated for one frequency, f1—that is H1(f1), φ1(f1), H3(f1), φ3(f1), H5(f1), and φ5(f1). However, it’s possible to obtain the kernels for a certain bandwidth by estimating the kernels for some frequencies within the bandwidth. With this approach, we have H1(f11), H1(f12) ... H1(f1n), F1(f11) … F1(f1n), H3(f11) ... H3(f1n) and so on. Finally, by doing a polynomial adaptation with these estimated values, we can obtain the kernels. However, it’s required that n be greater than the degree of the adapted polynomial.
Measurements and Results
Measurements are performed on a ZFL-1000H RF PA from Mini-Circuits. The chosen frequency band is 837 to 863 MHz, which is then divided into 10 narrowband frequency channels (the trial values shown in Table 1 are from 1.1 to 1.10). Each channel has a 20-kHz bandwidth. Furthermore, measurements are performed for two broadband frequency ranges, with bandwidths of 3 MHz (850 to 853 MHz) and 5 MHz (847 to 852 MHz), respectively.
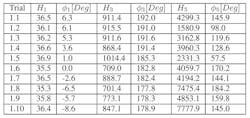
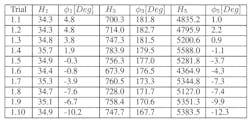
Table 1: Listed are estimated Volterra kernels at different frequencies for f1 using Method 1.
Method 1 Measurements
According to Method 1, to estimate the Volterra kernels H1(f), H3(f), and H5(f), it’s required to determine three points (Pin, Pout) on the power curve and three points (Pin, Fout) on the phase curve for the frequency f1.
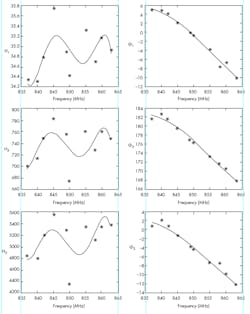
Table 1 shows the estimated Volterra kernels at different frequencies for f1 according to Method 1. Table 1 and Figure 7 show how the different components of the Volterra kernels vary with frequency.
7. Using Method 1, the estimated Volterra kernels are given at different frequencies, as is the frequency dependency of kernels for the bandwidth of 837 to 863 MHz.
We can see that H1 is almost constant—it only varies between 35.3 and 36.9. On the other hand, H3 varies more—somewhere between 700 and 1,100. The greatest variation is seen in H5, which varies between 1,500 and 8,000. The angles φ1 and φ3 are almost linear, whereas φ5 varies strongly. To estimate frequency dependency of the Volterra kernel within the bandwidth of 837 to 863 MHz, the estimated values from Table 1 were adapted in the following equations:
Figure 7 shows the result of these adaptations. We can see that the adaptation of H1, H3, H5, and φ5 is not precise. It’s likely that more precise results could be obtained by spending more time selecting the points. To determine the accuracy of the estimated results, we can compare these results to the broadband measurements.
From Equation 5, it’s possible to determine other frequencies (f3, f4, f5, and f6) when the two-tone frequencies, f1 and f2, are applied to the amplifier. Now, by substituting these frequencies in Equation 32, we can obtain kernel values for these frequencies. Substituting these values in Equation 5 gives us the calculated output. Finally, after all calculations are performed, we obtain the results (Figs. 8 and 9).
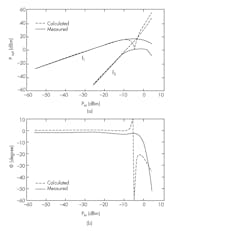
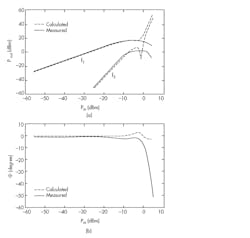
8. In this broadband measurement, f1 = 850 MHz and f3 = 847 MHz. Shown are measured and calculated Pout(Pin) curves at frequencies f1 and f3 (a), and measured and calculated angles of f1 (b).
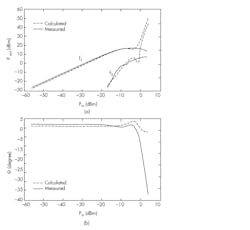
9. In this broadband measurement, f1 = 847 MHz and f3 = 842 MHz. Shown are measured and calculated Pout(Pin) curves at frequencies f1 and f3 (a), and measured and calculated angles of f1 (b).
In both cases, the calculated and measured power curves for f1 and f3 are perfectly matched up to input power levels of −10 dBm (Figs. 8a and 9a, again). Figure 8b reveals that the difference between the calculated and measured angles is about 2 to 3 degrees up to input power levels of −9 dBm. However, at input power levels greater than −9 dBm, the calculated angles deviate significantly from the measured values. For the other measurement, the difference between the calculated and measured angles is very small up to input power levels of −8 dBm (Fig. 9b). However, the difference starts to increase for input power levels beyond −8 dBm.
Method 2 Measurements
Next, 30 narrowband measurements for both the power curve (Pin, Pout) and the phase curve (Pin, φout) were performed. These values are applied to estimate the Volterra kernels, H1(f), H3(f), and H5(f), according to equation (28). Table 2 shows the estimated Volterra kernels.
Table 2: Listed are estimated Volterra kernels at different frequencies for f1 using Method 2.
10. Using Method II, the estimated Volterra kernels are given at different frequencies, as is the frequency dependency of kernels for the bandwidth of 837 to 863 MHz.
As Table 2 and Figure 10 show, H1 is almost constant—it only varies between 34.3 and 35.7. The variation of H3 is larger (between 670 and 790), while the largest variation occurs with H5 (between 4,300 and 5,600). All three angles variations behave almost linearly with the difference between the highest and lowest angles being 15 degrees. To estimate frequency dependency of the Volterra kernel within the bandwidth of 837 to 863 MHz, the estimated values from Table 2 were utilized in the following equations:
Figure 10 shows the result of these adaptations. For the adaptation, the highest polynomial of grade five is applied. Like Method 1, the adaptation did not work precisely. It’s probable that estimating the higher-order Volterra kernels would lead to more precise results. Here, the accuracy of the estimated results is again determined by comparing them to the broadband measurements (Figs. 11 and 12). The power curves show a good estimation for f1 up to input power levels of −2.5 dBm (Figs. 11a and 12a, again). However, at higher input power levels, the calculated values differ.
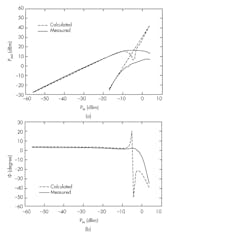
11. In this broadband measurement, f1 = 850 MHz and f3 = 847 MHz. Shown are measured and calculated Pout(Pin) curves at frequencies f1 and f3 (a), and measured and calculated angles of f1 (b).
12. In this broadband measurement, f1 = 847 MHz and f3 = 842 MHz. Shown are measured and calculated Pout(Pin) curves at frequencies f1 and f3 (a), and measured and calculated angles of f1 (b).
The calculated power curve for f3 is precise up to input power levels of −8 dBm. If a difference of up to 5 dB between the calculated and measured power curves for f3 was admissible, the calculated f3 up to an input power level of −2.5 dBm could be acceptable. Figure 11b reveals that the difference between the calculated and measured angles of f1 up to input power levels of +2.5 dBm is as high as 5 degrees. Furthermore, Figure 12b shows similar results for the other case.
Conclusion
This article presented two methods to estimate Volterra kernels by measuring power values in a specific frequency band and drawing power curves to determine the best points to formulate and calculate Volterra kernels. To demonstrate the efficiency and accuracy of the methods discussed, experiments were performed using an RF amplifier, the ZFL-1000H from Mini-Circuits. To assess the effectiveness of these methods, the outputs were calculated through the estimated kernels and the Volterra series for some specific inputs. The results were then compared with the measured outputs.
In Method 1, points (Pin, Pout) and (Pin, φout) were used to estimate the kernel values. The procedure for determining which points to use consist of studying the measured power curves, guessing, and testing.
In Method 2, the polynomial adaptation of measured power and phase curves were performed. Then, from these adaptation results, i.e., the coefficients of the polynomials, the kernel values were estimated. A comparison of these two methods revealed that Method 2 provides better results. In addition, Method 2 is easier and faster to perform.
Further research can be carried out to improve and develop these two methods. In Method 1, by spending more time selecting the points and using these points in relation to the amplifier’s compression point or intercept point, it’s possible to use these points for any other amplifier. In Method 2, it’s possible to estimate the higher-order Volterra kernels by increasing the degree of the adaptation polynomials, which is usually difficult to perform. In other words, the numerical problems may arise in the polynomial adaptation.
Siamack Ghadimi is involved with Research and Development at Infineon.
References
1. S. Ghadimi and T. Larsson, “Bestämning av Volterra-kärnor f¨or HF effekt förstärkare,” Master’s thesis, Lund University, Lund, Sweden, 1995.
2. M. Johansson, “Linearization of wideband RF power amplifiers using modulation feedback,” Ph.D. dissertation, Lund University, Lund, Sweden, Nov. 1995, lUTEDX/(TETE-1012)/1-65.
3. Y. Kuo, “Frequency-domain analysis of weakly nonlinear networks,” Circuits and Systems, vol. 11, no. 4, pp. 2-8, Aug 1997.
4. G. Einarsson, Olinijära system representerade med Volterra serier. Lund, Sweden: Lund University, 1971.
5. J. G. McRory and R. Johnson, “Volterra kernel estimation for mildly nonlinear amplifiers,” Electronics Letters, vol. 29, no. 23, pp. 2007–2008, Nov 1993.
6. T. T. Ha, Solid-State Microwave Amplifier Design. New Jersey: Wiley, 1981.
7. S. Boyd, Y. Tang, and L. Chua, “Measuring volterra kernels,” IEEE Transactions on Circuits and Systems, vol. 30, no. 8, pp. 571–577, Aug 1983.