This file type includes high resolution graphics and schematics.
Millimeter-wave frequency bands are attractive for their wide available bandwidths. There are a number of ways to generate these signals but, for each type of oscillator, it is desirable to be able to tune the source electronically, as well as in a defined and controlled manner. By using a suitable reactive device (such as a varactor diode) for tuning these millimeter-wave oscillators, the relationship between an applied voltage and the resulting frequency can be precisely defined. This can aid the design engineer in achieving the required spectral performance at these higher frequencies.
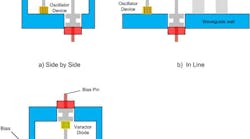
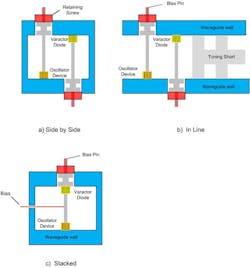
Oscillators developed for use at millimeter-wave frequencies are typically designed around waveguide housings. Electronic tuning of a waveguide-type oscillator can be accomplished in a number of ways, some of which are shown in Fig. 1. Additional information can be found in the technical literature (ref. 1) and in a recent article (ref. 2). The tuning sensitivity of a millimeter-wave varactor-tuned oscillator (VTO) can be estimated by means of relatively simple models, and this article hopes to provide some sights into the tuning relationship. Usually, the approach is to keep the fixed capacity with the varactor diode as large as possible, using the varactor diode to control the resonant frequency to the greatest extent.
1. These three VCO configurations show the circuits (a) side by side, (b) in line, and (c) stacked.
Related Articles
• Get A Handle On Oscillator Phase Noise And Jitter
• YIG Oscillators Fit Surface-Mount Packs
• SAW Oscillator Clocks To 1090 MHz
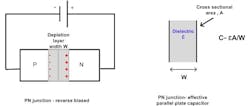
A varactor diode is essentially an active device with positive-negative (PN) junction which has reverse bias applied. This results in a movement of charge carried away from the junction, so that this region is referred to as the depletion layer. The depletion layer has charge on either side of the junction and acts like a parallel-plate capacitor (Fig. 1). The capacitance relationship for a parallel-plate capacitor is C = εA/W, where:
A = the effective cross-sectional area of the device,
ε = the relative dielectric constant of the depletion layer, and
W = the width of the depletion layer.
Application of a voltage results in an increase of the depletion layer width, affectively altering the capacitance (Fig. 2).
2. These drawings show the depletion layer of a varactor diode (left) and how its capacitance can change with applied voltage (right).
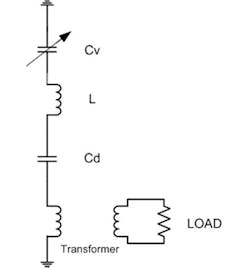
The typical fabrication process for a varactor diode results in a device with a mesa structure. This device can be mounted in a number of different standard and custom housings to simplify handling. The junction capacitance and associated parasitic circuit elements can be included in a simple equivalent circuit (Fig. 3) for modeling and simulation purposes.
3. The drawing (left) represents a packaged diode along with its equivalent circuit (right).
The selection of a suitable semiconductor device for a varactor diode can make an impact on the performance of the diode, although this receives little coverage in the literature. Varactors are true diodes with a clearly defined junction, which can be characterized by means of a particular doping profile; this is effectively captured in the gamma parameter for each varactor diode. The gamma parameter can be placed in two categories: abrupt and hyperabrupt. Quite simply, a varactor diode is effectively a variable reactance which is a function of some applied DC tuning voltage. More detailed models of varactor diodes are available in the literature, which are useful for a specific package or unpackaged devices. To obtain a general understanding of a varactor diode’s behavior, it is a reasonable to ignore packaging and parasitic affects in the first instance, as this allows the designer to appreciate the merits of such devices.
This basic approach leads to the following expression:
Cv + kV –Γ (1)
where:
V = control voltage;
k = a constant;
Cv = varactor capacitance; and
Γ = the gamma or doping profile.
This file type includes high resolution graphics and schematics.
For the basic resonant structure shown in Fig. 4, Cv is the varactor capacitance, Cd is the circuit capacitance, and L is the total inductance of the structure.
4. This simplified resonant circuit includes the key circuit elements.
For the case where the circuit capacitance is much greater than the varactor capacitance, or if Cd << Cv:
F ≈ (L/Cv)0.5 → F = K/(Cv)0.5 (2)
where:
F = the resonant frequency;
L = the circuit inductance; and
K= a constant.
Combining Eqs. 1 and 2 yields an expression between frequency and voltage:
F = K/[k(V)Γ → ≈ VΓ/2
It can be seen that combining eqs. 1 and 2 yields an expression between frequency and voltage.
This very simplistic approach provides a basic relationship between frequency and the applied voltage, with Γ representing a doping constant, equal to 0.5 for an abrupt diode and 1.0 or 1.25 for a hyperabrupt diode:
Γ = 0.5 → F ≈ V0.25
Γ = 1.0 → F ≈ V0.50
Γ = 2.0 → F ≈ V
In reality, it is difficult to achieve a diode capable of Γ = 2.0, although devices with values equal to 1.0 and 1.25 are commercially available. Figure 4 indicates the ideal behavior of frequency with voltage variation for a few varactor doping profiles.
5. Frequency variations can occur due to variations in varactor diode voltage.
A more detailed analysis3 of a varactor’s influence on frequency tuning can be complicated. This is due to the issues of the varactor construction and device to device variation, as can be seen in Fig. 5. Package assembly and parasitic circuit elements can have profound effects at high frequencies in particular the type and shape of the internal bond wires. For this analysis, a number of commercially available packaged varactor diodes were procured and installed into a W-band Gunn oscillator to compare performance levels.
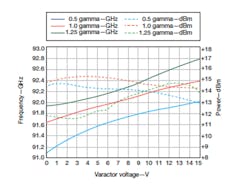
Although the varactor package type was the same in each case, each device package had its own subtle differences in dimensions as well as in internal construction, no doubt with ramifications at the higher frequencies. Difference between sources can occur because of variations in reactance and skin effect due to fringing fields, the lengths of current paths, and various parasitic effects. No serious efforts were made to optimize the circuit, particularly for power. The measured performance is shown in Fig. 6.
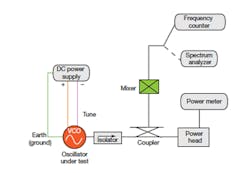
6. This block diagram shows the instruments needed for the VCO test system.
When Figs. 4 and 6 were compared, some good correlation could be seen between the tuning profiles. The gamma parameter impacts the variation of frequency with voltage—hence the tuning sensitivity. This would suggest that the crude model has some benefit in providing some insight into designing and developing a varactor tuned oscillator with a specific tuning sensitivity.
7. These curves show the changes in frequency for different applied varactor voltages.
The crude model and measured data demonstrate that the tuning sensitivity (and thus, linearity) can be influenced significantly by the selection of a suitable varactor diode. This also opens the possibility of tailoring the doping profile of the varactor diode to achieve a specific tuning sensitivity; this could be achieved during the semiconductor fabrication process. However, in practice, linear tuning must take into account circuit and oscillator characteristics as well as the varactor diode.
Saabra Deen, Design Engineer
Osctek Ltd., Harrow, Middlesex, United Kingdom; +44 (0) 2084207043, e-mail: [email protected], www.osctek.com.
References
1. Jack Holzman and D. Robertson, Solid-State Microwave Power Oscillator Design, Artech House, Norwood, 1992, www.artechhouse.com.
2. Saabra Deen, “Designing Compact V/W-Band Gunn Sources, Microwaves & RF, April, 2011, p. 82.
3. Joseph F. White, Semiconductor Control, Artech House, Norwood, 1978, www.artechhouse.com.
4. David M. Pozar, Microwave Engineering, 2nd ed., Wiley, New York, 1998.
5. G.S. Hobson, The Gunn Effect, Clarendon Press, Oxford, England, 1974.
6. J.S. Panesar, private communication.
This file type includes high resolution graphics and schematics.