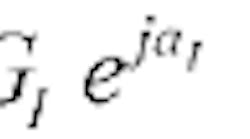Phase modulation is the basis for many modern mobile telecommunications formats, including IS-136 and GSM. Using in-phase (I) and quadrature (Q) signal components, modulation is commonly generated by means of an analog I/Q modulator. Since variations in components and manufacturing processes can easily introduce imbalance in I/Q modulator arms, resulting in poor transmission quality, I/Q imbalance measurements are critical to maintaining good system performance. This report will examine such measurements and highlight why traditional measurements can be misleading, offering an improved, alternative approach which can be applied to existing test processes.
Figure 1 shows a model for data transfer in a digital wireless-communication system. The particular modulation format is not critical here; the important assumption is that the data modulator creates complex signals with I and Q components. The I and Q components can be treated as a complex number, with I being the real part and Q being the imaginary part of the complex number. As a convention, complex quantities will be underlined throughout for clarity.
Since a complex signal cannot be transmitted, it must be converted to a real value and modulated onto a carrier signal. The I/Q modulator provides the means for this. An I/Q modulator consists of a local oscillator (LO) feeding two (I and Q) mixers. The LO signal that feeds the Q mixer is shifted by +p/2 rad. in phase relative to the LO signal that feeds the I mixer. The mixers' outputs are combined to form the complex signal.
Due to differential additional aI and aQ phase shifts along the path leading to the mixer, the phase shift might not be exactly +p/2 rad., however. Due to different gains, GI and GQ , the two mixers may also receive LO signals at different levels, further complicating matters. These errors can be expressed by the complex gains of Eqs. 1 and 2.
Due to leakage, some portion of the LO signal may also appear at the output of the mixers. Such leakage can stem from various sources, which are not discussed here, but it can be represented by additive offsets, OI and OQ, to the in-phase and quadrature-phase input signals, respectively. These errors are traditionally characterized by the measures of Eqs. 3-5. Ideally, Eqs. 3 and 4 should be 0 dB.
In Eq. 5, O is called the "complex origin offset" and is shorthand for the expression in Eq. 6.
In Eq. 5, Ps is the average power of the baseband input signal s(t) . Ideally, this measure should be as low as possible. In practice, this is -30 dB or lower.
The RF channel incorporates all the RF components between the I/Q modulator and I/Q demodulator. As a simple but usable model (especially in manufacturing where the mobile units are connected to test equipment by means of a cable), this signal path is considered to be free of distortion. The signal path is assumed without loss of generality to have 0 dB gain and 0 group delay. As part of the RF signal chain, the I/Q demodulator, which translates a received signal back to complex baseband signals, is also considered to be ideal for modelling purposes. Additional assumptions are that the LO for the I/Q modulator has unit amplitude while the LO for the I/Q demodulator has an amplitude of two units, and that both LOs have a starting phase of 0 when time, t, is 0.
In this model, the received complex baseband signal, r(t) , can be described by Eq. 7. The Re{s(t)} and Im{s(t)} operators return the real (I) and imaginary (Q) components of the baseband input signal, s(t), respectively.
Generally, the aim of an I/Q modulator characterization is to measure gain imbalance, quadrature skew, and LO leakage since these parameters are used in I/Q modulator data sheets, and because manufacturers often provide some adjustable devices (e.g., potentiometers) that are dedicated to reduce these errors. Equation 7 provides a way to determine the imbalances via estimation of the GI , GQ , and O intermediate parameters. Once GI , GQ , and O are obtained, the gain imbalance, quadrature skew, and LO leakage can be calculated with Eqs. 3, 4, and 5.
Equation 7 contains the three unknowns GI , GQ , and O, so three independent equations are needed to solve them. This can be accomplished by capturing three samples of the transmitted complex baseband signal, s(t), and the corresponding three samples of the received complex baseband signal, r(t).
The received complex baseband signal, r(t), is determined directly by sampling the received signal from a device under test (DUT) at the output of the I/Q demodulator. However, the transmitted signal, s(t) , is not readily available. It is synthesized in the measuring device from the received digital data, which can be recovered by demodulating r(t). This synthesized signal is denoted as s'(t).
Unfortunately, all digital modulation formats are designed so that the absolute phase is always irrelevant. This is necessary because the phase at the receiving end is always random. Hence, there is an infinite number of s'(t) that carry the same digital content as the actually transmitted s(t), differing only in phase. They can be rotated into the actually transmitted signal, s(t), by a phase shift, d, shown in Eq. 8.
As a result, the system of equations that is solved is Eq. 9 rather than Eq. 7. The question is whether this phase ambiguity, d, affects the measurement results or not. Substituting Eq. 8 into Eq. 7 and expanding yields Eq. 10.
Comparing this with Eq. 9 reveals the relationship between G'I, G'Q, O' calculated using the synthesized transmitted signal, s'(t) , and the actual GI, GQ, O and shown in Eqs. 11-13.
Based on these results, the relationships between the perceived GainImbalance', QuadratureSkew', LOLeakage', and the actual GainImbalance, QuadratureSkew, LOLeakage are shown in Eqs. 14-16.
Equations 14 and 15 show that the calculated gain imbalance and quadrature skew do differ from their actual values if d != 0, that is, if the synthesized transmitted signal, s'(t), differs in phase from the actual transmitted signal, s(t).
Page Title
To eliminate this phase ambiguity, the phase reference of the actual transmitted signal, s(t), must be entered into the measurement equipment as a reference. Unfortunately, this information is difficult to obtain because it is irrelevant as far as the digital communication is concerned. Therefore, it is rarely standardized and, by the same token, it is not very well documented.
It is possible to determine this phase empirically using an I/Q modulator whose gain imbalance and quadrature skew are some known, but nonzero values. However, different mobile-station models might use different phases. In addition, this phase might change without notice over time.
Worse still, even the assumption that the phase is constant might not be true. It may change randomly or semirandomly burst by burst. This is the worst-case scenario because it implies that the phase is impossible to track and take into account. As a result, the gain imbalance and quadrature skew figures change randomly burst by burst. This makes I/Q tuning difficult and averaging measurement results (to obtain more accurate results) impossible.
Searching for an alternative measure to replace gain imbalance and quadrature skew, it is helpful to look at how traditional I/Q modulator tuning is performed. The I and Q channels are driven with in-phase and quadrature-phase sine waves. Using complex number notation, this signal is simply a complex single-tone signal at +ω frequency in Eq. 17.
Using a spectrum analyzer to monitor the output of the I/Q modulator, a perfect I/Q modulator would only show a tone at Ω + v frequency, where Ω is the LO frequency of the I/Q modulator. An imbalanced I/Q modulator, however, exhibits three tones at the output: the desired component at Ω + v and two spurious components at Ω and Ω − v frequencies (Fig. 2). The Ω component is called LO leakage, which, as defined by Eq. 5, represents the ratio of the spurious signal power at Ω to the desired signal power at Ω + v. The Ω − v component results from both the gain imbalance and the quadrature skew.
Looking at the I/Q imbalance measurements from this perspective, it is interesting that the phase issue is absent. The spectrum analyzer is not synchronized with the signal sources. Each time the spectrum analyzer sweeps through the spectrum; the I/Q modulator is driven by a tone with a different phase, φ. Still, a steady consistent reading is apparent when looking at the power of these tones in the signal analyzer. This suggests that a new measure, called "I/Q imbalance," could be used as the ratio of the spurious signal power at Ω − ω to the desired signal power at Ω + ω, analogously to the LO leakage definition. It is easy to obtain its definition by substituting Eq. 17 into Eq. 7, which, after rearrangement, yields Eq. 18.
Notice that this formula describes the received signal at the output of the I/Q demodulator as seen in Fig. 1. The frequency components Ω + ω, Ω, and Ω − ω at the output of the I/Q modulator are mapped to −ω, 0, and +ω at the output of the I/Q demodulator. With this in mind, the new measure is simply Eq. 19.
What is needed now is a conversion formula that converts the GainImbalance′ and QuadratureSkew′ readings provided by the measurement instruments into meaningful data. This can be obtained from Eq. 21 by using the definitions of gain imbalance and quadrature skew to derive Eq. 22.
One might wonder how this solves the problem of not being able to measure gain imbalance and quadrature skew without knowing the phase reference of the transmitted signal. However, not knowing this phase simply means that the obtained gain imbalance and quadrature skew measures are meaningless if one wants to relate them directly back to the I/Q modulator model of Fig. 1. They can still be used to calculate the I/Q imbalance measure. Since the I/Q imbalance parameter is independent of this phase, these incorrect gain imbalance and quadrature skew parameters yield the same I/Q imbalance measure. So, if the phase of the ideal baseband signal is assumed incorrectly, or worse still, if this phase changes randomly, the I/Q imbalance figure still remains a constant value.
The I/Q imbalance measure defined by Eq. 22 is completely analogous to the image-frequency power measure traditionally used for tuning I/Q modulators. This means that the same tuning procedures developed for this traditional technique can be used with the new I/Q imbalance metric.
The I/Q imbalance metric has the great advantage that it makes no assumption about the test signals driving the I/Q modulator. It can be a sine wave, but equally, it can be a complex modulated signal. It is therefore possible to perform the I/Q modulator tuning procedure while transmitting real data. This avoids the need for a special test mode required by the traditional method.