This file type includes high resolution graphics and schematics when applicable.
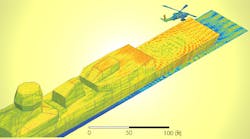
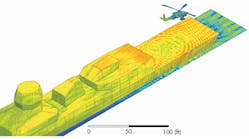
What approaches would you take to electromagnetically (EM) simulate a large and/or complex structure or system? This question commonly faces engineers working on radar, macro-antenna placement, aircraft, or satellites. The dilemma also arises in scenarios where there are design geometries that are complex or tens to hundreds of times the wavelength of the frequencies of interest (Fig. 1).
Until recent advances in computational methods, hardware, and intelligent computing, the answer was to simplify the problem until it could be managed with available technologies.
But this approach is often inadequate for predicting even minor coupling or edge effects. For high-frequency or broadband simulations, the computation time could be enormous, as well.
“As the electrical size (as measured in wavelengths) of an object increases, memory requirements and run time for full-wave techniques—such as method of moments (MoM), finite-difference time domain (FDTD), finite element method (FEM), finite integral technique (FIT), etc.—increase rapidly,” says Matthew Miller, president of Delcross Technologies. “At some point, it is no longer practical to use a full-wave solver. It is at this point that users typically switch to an asymptotic, ray-based solution, such as geometric theory of diffraction (GTD) or physical theory of diffraction (PTD; Fig. 2).”
These techniques combine the physical mechanics of high-frequency or photonic ray/current properties with physics-based descriptions of interaction with conductors and induced currents. PTD (also known as the Physical-Optics solver method) relies on estimating the electric field on a conductor’s surface using ray optics. The approximated field results are then integrated over the surface to derive the resultant scattered field. The areas that are not illuminated by the EM rays are considered to have zero current and effect.
Such PTD methods are effective for large structures that have arbitrary or complex surfaces or structures with poorly reflective surfaces. For example, PTD can be used to analyze large-reflector antenna radiation patterns and radar cross sections of large aerospace or naval structures based upon their scattering performance. Many modern EM-simulation software suites include corrections to the PTD method to account for creeping waves in shadowed regions, current corrections on edges and corners, and plane-wave basis functions. By compensating in this manner, the software suites increase computational efficiency.
A drawback of the PTD method is the exponential growth of computational requirements as the number of reflections multiplies. This factor necessitates the use of less physically accurate methods in those scenarios.
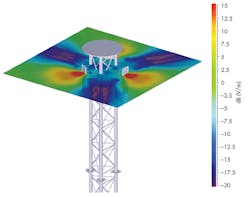
Because PTD relies on induced currents, it acts as a bridge between a full-wave solver (such as FEM or MOM) and a non-wave solver (like GTD). GTD, also known as Geometric Optics/Shooting and Bouncing Rays (SBR), uses both the ray-based optical propagation theory and the theory of reflection and refraction. The latter is used to model metallic and dielectric structures that are 10 times larger than the wavelength of interest (Fig. 3).
With GTD, the contact point for an object’s bouncing ray is calculated for reflection, refraction, and transmission on the material boundaries. This behavior enables the GTD method to respond accurately to multiple layered objects, such as a dielectric-coated metallic surface.
The GTD approach also scales efficiently in response to the resource requirements of complex scattering problems and multiple reflections. Both path and geometric complexity ultimately increase the computational resources needed by the GTD method. To reduce the resource demand, simple primitive shapes will often be used to replace more complex surfaces, such as a rounded cone for the front of an aircraft. When size is the limiting factor computationally, methods like the Uniform Theory of Diffraction (UTD) can be used on simple structures more efficiently than PTD and GTD.
The UTD method uses quasi-optical approximation of near-field EM fields to take advantage of ray diffraction techniques. In doing so, it can estimate the diffraction coefficients of a combination of structure sources. The fields calculated from the phasors, which are generated from the diffraction coefficients, are then combined with incident and reflected fields for a complete field solution. Generally, the UTD method only operates well with structures composed of flat polygons or simple cylinders, where the geometry’s edge dimensions are as long or longer than a wavelength.
A lot of the asymptotic methods fail at smaller and more complex structures. Yet many modern EM-simulation software offerings do feature dual simulation, which allows different components of a structure to be simulated with a combination of full-wave and asymptotic methods. “One strategy is to link between full-wave methods, like FEM or MoM, and asymptotic methods, like PO,” notes Matt Commens, lead product manager for HFSS ANSYS, Inc. “This approach can provide the balance between accuracy and rigor with detailed components in terms of size and scalability for platform analysis.”
As long as it has a solving pattern that is similar to the one used by the solutions, this approach allows fields or currents at the boundaries to transfer continuously from one domain to another. An example of a hybrid approach is simulating a complex antenna structure, such as a 3D feed horn, in close proximity to a large metallic object, such as a reflector dish or fuselage. The full-wave solver would operate in the region around the complex structure. In contrast, the asymptotic method would account for the area in between the structures and across the surface of the larger structure.
Hybrid methods are capable of reducing simulation time and resources. Yet the complexity and sheer size of the structures in a simulation are often beyond common computational resources. Here, clever computation and hardware techniques can be used to increase computational capacity. One of these techniques, known as parallel processing, divides the computational effort of a simulation onto multiple cores. This can be done as a division of frequency steps or as a subdivided segment of meshes, known as Domain Decomposition Method (DDM).
“With modern techniques and hardware, it is not out of the question to solve for the antenna with the platform and even solve for interactions between platforms,” says Commens. “An example of this is a helicopter in close proximity to a ship, where the interaction between antennas is modeled with the finite-element method and domain decomposition method (DDM). A visualization of the surface currents on the helicopter and ship platforms is established by a VHF antenna, which is located on the tail boom of the helicopter.”
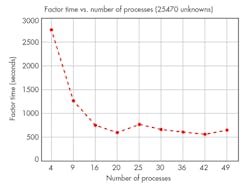
These methods require that the EM simulator be specifically designed for parallel processing to have significant efficiency. Inevitably, parallel processing is less than 100% efficient when it comes to dividing computational resources (Fig. 4).
This file type includes high resolution graphics and schematics when applicable.
Beefing Up Processing
This file type includes high resolution graphics and schematics when applicable.
A constant challenge for EM simulations is that the simple computer can only house a finite amount of random-access memory (RAM), storage space, and processing power. Leveraging the power of multiple computers can thus reduce computation time to a small fraction of what would traditionally be possible. Keep in mind that many solver methods require that RAM be scaled as the problem size scales. Given the minimum wavelength of the problem, distributed/shared memory methods also exist.
This approach divides the memory blocks of a simulation into various nodes within a cluster computing system. For many of these multi-node computing systems, a limiting factor of the simulation is the intercommunication capability between the nodes. Some EM-simulation software suites use techniques that enable a node to run relatively autonomously until a solution is produced and the results are aggregated.
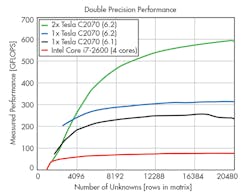
More recently, the highly specialized and core-abundant processing capability of a graphics-processing unit (GPU) also has been used to provide more processing units for an EM simulation. GPUs are traditionally used to compute massive amounts of parallel data in terms of vectors or matrices for the rendering of graphics and video. Compared to CPUs, they contain less control hardware. In fact, the standard GPU contains anywhere from hundreds to thousands of core processors.
The bulk of computations needed for EM simulations are large numbers of simple arithmetical computations to solve for differential, integral, and matrix systems of equations. As a result, GPUs are well suited to the task—so long as the necessary software exists to support the offloading of the simulation computations onto the GPU (Fig. 5). NVidia is piloting such a software infrastructure for its GPUs, called CUDA, which many simulation software companies are embracing.
For all of the numerous solutions and offering now available, extremely massive or complex simulations still present a major challenge. It is unmanageably costly to house the necessary computational resources to simulate such structures with sufficient accuracy. The cloud at least offers an alternative to purchasing, setting up, and maintaining a private local computing station.
These services can allow for either the software and hardware or just hardware offloading of resources to distributed computing resources [often known as high-performance computing (HPC)]. Some of these services come equipped with the software pre-installed, which means that just servicing or licensing fees are needed to use the computational resources on a subscription or per-use basis.
This file type includes high resolution graphics and schematics when applicable.