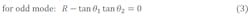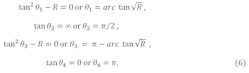Ultrawideband (UWB) communication systems offer great promise for transferring high-speed data, provided that proper filtering can be achieved to prevent interference. Since the Federal Communications Commission (FCC) established the UWB spectrum for commercial use in 2002,1 various UWB system topologies have been developed for use from 3.1 to 10.6 GHz, with a corresponding need for UWB bandpass filters. In late 2003, the first UWB filter was documented, using microstrip ring resonators with loaded open stubs to achieve dual stopbands.2
The use of multiple-mode resonators (MMRs) has supported a new generation of UWB filters. For example, refs. 3 and 4 detail a stepped-impedance MMR with half-wavelength λ/2 low-impedance segments at the center and two identical quarter-wavelength λ/4 high-impedance segments at both sides, which allocated its three resonant modes within the UWB frequency range. Subsequently, an UWB bandpass filter was proposed with nonuniform coplanar-waveguide (CPW) MMR with short-circuited ends.5
Another UWB filter was realized by loading three open stubs in parallel with a conventional MMR resonator in the center and two symmetrical locations, respectively.6 This approach exploits the first four resonant modes of the MMR for relocation within the UWB frequency range while pushing up the fifth resonant mode to create a wider upper stopband. Also, electromagnetic-bandgap (EBG) embedded MMRs were applied to the design of UWB filters for improved upper stopband performance.7 In addition, by attaching three pairs of circular impedance-stepped stubs in parallel to a high-impedance microstrip line, an MMR capable of supporting a wide passband and stopband was developed.8 Similarly, the use of a spiral-shaped loaded multiple-mode resonator also shrinks the size of a wideband bandpass filter circuit while enhancing its bandwidth.9The current author has proposed numerous filter topologies based on folded stepped-impedance resonators (FSIRs) with parallel high-impedance segments to achieve a compact notched UWB bandpass filter and an UWB lowpass filter with wide stopband.10-12
In the present report, a compact UWB bandpass filter structure was developed. It consists of folded multiple-mode resonators coupled to each other and to SIRs using a parallel coupled configuration; the feedlines are tapped off the SIRs. The proposed filter features a wide passband response from 3.1 to 10.6 GHz that meets the FCC’s limits for handheld and indoor UWB communications devices. In addition, it exhibits an extremely wideband stopband with 20-dB rejection extending to U-band frequencies. By using transmission zeros produced by tapped parallel-coupled lines, higher-order resonant modes, due to the harmonic nature of a stepped-impedance MMR resonator, can be sufficiently quelled to create a broad stopband.
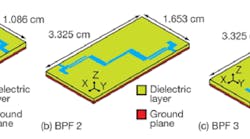
1. These three layouts show the topologies of the three UWB bandpass filters: (a) one-pole BPF 1, (b) two-pole BPF 2, and (c) folded two-pole BPF.
Figures 1(a), (b), and (c) show three UWB filter topologies (named BPF 1, BPF 2, and BPF 3, respectively). The design in Fig. 1(a) uses an MMR which is coupled to SIRs using a parallel coupled configuration. The folded MMR has resonance characteristics similar to those of a stepped-impedance MMR, although the folded MMR contributes to both size reduction and upper-stopband improvement. The filter was designed and fabricated on RT/duroid® 5880 circuit material from Rogers Corp. with relative permittivity (dielectric constant) of 2.20, thickness of 1.52 mm, and loss tangent (dissipation factor) of 0.0009.
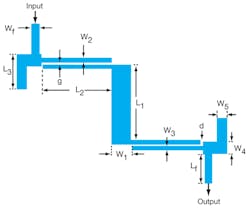
2. This layout shows the structural parameters for the proposed UWB BPF.
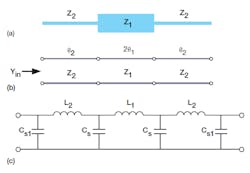
3. This schematic diagram of the stepped-impedance MMR (a) is shown besides its equivalent-circuit model (b) and its LC equivalent-circuit model (c).
Figure 2 illustrates the layout of the proposed UWB BPF with its structural parameters. Figures 3(a), (b), and (c) show the geometry, equivalent-circuit model, and inductive-capacitive (LC) equivalent-circuit model of the basic open-circuited stepped-impedance MMR. It consists of a low-impedance line section in the middle with characteristic impedance Z1 and electrical length θ1, along with two identical high-impedance line sections with characteristic impedance Z2 and electrical length θ2 on both sides. The input admittance (Yin), viewed from the open end, can be derived from Eq. 1:
The resonance condition can be derived from the following:
The fundamental and higher-order-mode resonances occur alternately in the odd and even modes and can be obtained from electrical lengths θ1 and θ2 by the following two transcendental equations:
By choosing θ1 = θ2 = θ and streamlining the design equation, the following can be derived from Eq. 1:
where Rz = Z2/Z1 is the impedance ratio of the stepped-impedance MMR. With the fundamental and higher-order-mode resonances represented by fm1, fm2, fm3, and fm4, with corresponding electrical lengths of θ1, θ2, θ3, and θ4, it is possible to obtain the following using Eqs. 1 and 2:
Thus:
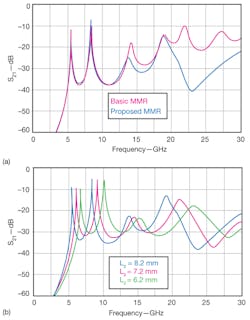
In the filter design, the impedance ratio and first resonant mode are set by means of Rz = 2.05 and fm1 = 5.65 GHz. From Eq. 5, the frequency ratios fm2/ fm1, fm3/ fm1, and fm4/ fm1 can be selected nearly as 1.6, 2.3, and 3.3, respectively. Once Rz is determined, the high-impedance segments of the MMR can be folded to achieve a more compact design. Figure 4(a) shows simulated frequency-response curves for the basic and folded MMRs under weak capacitive coupling. The resonators have similar behavior—with four resonant modes distributed around 5.61, 8.44, 13.57, and 18.85 GHz—validating the theoretical analysis. The folded MMR is capable of yielding transmission zeros at higher frequencies, contributing to good upper-stopband performance.
4. These plots show (a) the simulated S21 responses of the proposed and basic MMRs, and (b) the simulated S21 responses for the proposed MMRs with different values of L2.
Several degrees of freedom exist for adjusting the location of the resonant modes. Figure 4(b) shows the simulated forward-transmission (S21) response of the proposed MMRs with different values of length L2. From Fig. 4(b), as L2 increases, the resonances shift lower in frequency. For tighter coupling between input and output resonators using the proposed MMR designs, the parallel-coupled structure of Fig. 5(a) was used. This feed structure is composed of two FSIRs that are capacitively coupled, and the I/O lines are tapped off the SIRs as shown. Capacitive coupled structures or parallel-coupled lines have been widely evaluated in multistage wideband filters because of their simple design procedure.13 The drawback to this approach is its practical limitations. For wideband filters, the space between the coupled lines must be minimized for tight coupling, and it is difficult to realize such small gap spacing in typical manufacturing processes.
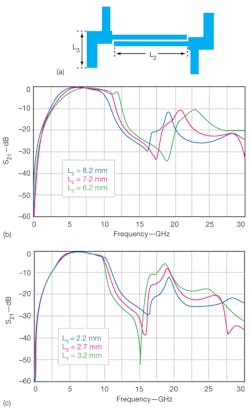
5. The schematic diagram of (a) the proposed coupling structure is shown next to (b) the simulated S21 responses for the proposed coupling structure with different values of L2 and (c) simulated S21 responses for the proposed coupling structure with different values of L3.
The proposed feed structure offers advantages over conventional approaches, including a wider and sharper stopband region. A tapped-line I/O structure is part of this approach. Also, since the first and last portions of the filter have been eliminated, a design with tapped I/O ports can save space on a printed-circuit-board (PCB) design. The position of the tapped-line I/O port is optimized for higher rejection in the stopband. To better understand the impact of different feed parameters on the frequency response of the feed structure, simulated S-parameters were calculated for different dimensions of L2 and L3 as shown in Figs. 5(b) and (c), respectively. One transmission zero is located at about 16.09 GHz, but its location and rejection level can be adjusted by changing the values of L2 and L3.
As can be seen from Fig. 5(b), when L2 decreases from 8.2 to 6.2 mm in 1-mm steps, and the other parameters remain fixed, the coupling transmission zero will move higher in frequency. From Fig. 5(c), it is obvious that by increasing L3 from 2.2 to 3.2 mm in 0.5-mm steps, the coupling zero will decrease in frequency with a deeper rejection level.
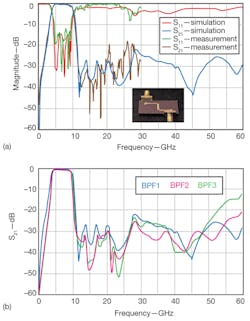
With the above-described features, it is feasible to control the resonant modes of the proposed resonator and transmission zeros of the designed coupling structure by tuning their structural parameters. Figure 6(a) shows full-wave simulated and measured S-parameter for the proposed UWB bandpass filter, where the physical dimensions are Lf = 1 mm, L1 = 6.7 mm, L2 = 8.2 mm, L3 = 2.2 mm, Wf = 1.0 mm, W1 = 1.6 mm, W2 = 0.2 mm, W3 = 0.7 mm, W4 = 1.4 mm, W5 = 1 mm, g = 0.13 mm, and d = 0.1 mm. Obviously, Fig. 6(a) shows that the filter’s 10-dB passband effectively spans 3.1 to 10.6 GHz.
6. These plots show (a) the simulated and measured S-parameter responses with frequency for the proposed filter, accompanied by a photograph of the fabricated filter and (b) a comparison of S-parameter responses for filters BPF 1, BPF 2, and BPF 3.
The new filter topology has several advantages over the conventional MMR-based UWB bandpass filter of ref. 3, including higher passband return loss, a sharper response, and wider stopband. The table compares the current design with a number of previously reported UWB bandpass filters. To improve the out-of-band performance in both the lower and upper stopbands of the current design, another MMR could be coupled with the first MMR via coupled lines, as shown in Figs. 1(b) and (c). Simulated S-parameters for these respective filter designs (BPF 2 and BPF 3) are shown in Fig. 6(b) for comparison with the original design, BPF 1. In a case where compact size is required, BPF 1 is more appropriate. But for an application requiring a sharper response and higher rejection level in the stopband, both BPF 2 and BPF 3 are useful. However, BPF 3 offers a more compact size.
In summary, the new UWB bandpass filter design features a wide upper stopband and low insertion loss throughout the passband of 3.1 to 10.6 GHz, with no more than 0.28-dB loss ripple. The return loss is better than 12.26 dB and the stopband rejection is better than 20 dB. The filter is quite small—approximately 0.79λg × 0.36λg—where λg is the guided wavelength at 6.85 GHz.
Milad Mirzaee, Research Engineer
Department of Electrical and Electronics Engineering, Eslamabad-E-Gharb Branch, Islamic Azad University, Eslamabad-E-Gharb, Iran; e-mail: [email protected].
Bal S. Virdee, Professor of Microwave Communications
London Metropolitan University, Center for Communications Technology, Faculty of Life Sciences and Computing, London, England.
References
1. Federal Communications Commission (FCC), Revision of Part 15 of the FCC’s Rules Regarding Ultra-Wideband Transmission Systems, First Report and Order, ET-Docket 98-153, FCC 02-48, April 2002.
2. H. Ishida and K. Araki, “Design and analysis of UWB bandpass filter,” in Proceedings of the IEEE Topical Conference on Wireless Communications Technologies, October 2003, pp. 457-458.
3. L. Zhu, S. Sun, and W. Menzel, “Ultra-wideband (UWB) Bandpass Filters Using Multiple-mode Resonator,” IEEE Microwave and Wireless Components Letters, Vol. 15, No. 11, November 2005, pp. 796-798.
4. S. Sun and L. Zhu, “Capacitive-Ended Interdigital Coupled Lines for UWB Bandpass Filters with Improved Out-of-Band Performance,” IEEE Microwave and Wireless Components Letters, Vol. 16, No. 8, August 2006, pp. 440-442.
5. J. Gao, L. Zhu, W. Menzel, and F. Bogelsack, “Short-Circuited CPW Multiple-Mode Resonator for Ultra-Wideband (UWB) Bandpass Filter,” IEEE Microwave and Wireless Components Letters, Vol. 16, No. 3, March 2006, pp. 104-106.
6. R. Li and L. Zhu, “Compact UWB Bandpass Filter Using Stub-Loaded Multiple-Mode Resonator,” IEEE Microwave and Wireless Components Letters, Vol. 17, No. 1, January 2007, pp. 40-42.
7. J. Garcia-Garcia, J. Bonache, and F. Martin, “Application of electromagnetic bandgaps to the design of ultra-wide bandpass filters with good out-of-band performance,” IEEE Transactions on Microwave Theory & Techniques, Vol. 54, No. 12, December 2006, pp. 4136–4140.
8. B. Yao, Y. Zhou, Q. Coa, and Y. Chen, “Compact UWB bandpass filter with improved upper-stopband performance,” IEEE Microwave and Wireless Components Letters, Vol. 19, No. 1, January 2009, pp. 27-29.
9. M. Nosrati, and M. Mirzaee, “A compact wideband microstrip bandpass filter using quasi-spiral loaded multiple-mode resonator,” IEEE Microwave and Wireless Components Letters, Vol. 20, No. 11, November 2010, pp. 607-609.
10. M. Mirzaee, “A novel small ultra-wideband bandpass filter including narrow notched band utilizing folded-T-shaped stepped impedance resonator,” Progress in Electromagnetics Research C, Vol. 22, June 2011, pp. 85-96.
11. M. Mirzaee, “UWB Lowpass Filter Features Wide Stopband,” Microwaves & RF, Vol. 51, No. 3, March 2012, pp. 74-78.
12. M. Mirzaee, “SIR Cells Support UWB Lowpass Filter,” Microwaves & RF, Vol. 51, No. 6, June 2012, pp. 77-83.
13. G.L. Matthaei, L. Young, and E.M.T. Jones, Microwave Filters, Impedance-Matching Networks, and Coupling Structures, Artech House, Norwood, MA, 1980.