Download this article as a .PDF
Generating radar signals can be challenging for any test signal generator. Radar technology, which was once primarily used for military applications, is becoming a standard feature in the collision-avoidance systems of an increasing number of commercial vehicles. Testing these systems requires a signal source capable of combinations of carrier frequency, modulation bandwidth, and tightly controlled pulses that can be difficult to produce.
The need to emulate multiple-antenna radar systems based on phased-array antennas—or, more recently, multiple-input, multiple-output (MIMO) antenna architectures—makes it necessary for a radar test signal source to generate multiple signals with tightly controlled timing and phase alignments.
Radar signals have traditionally been produced by means of a baseband signal generator and an RF/microwave modulator. However, with the emergence of high-speed, high-frequency arbitrary waveform generators (AWGs) based on high-speed digital-to-analog converters (DACs), it is now possible to directly generate radar signals with carrier frequencies to 20 GHz (beyond Ku-band frequencies). In contrast to the baseband/modulator approach, the use of an AWG delivers higher signal quality, greater repeatability, and much better cost-effectiveness than traditional radar signal generation options.
Before looking at how AWGs can be applied to radar signal generation requirements, however, it’s helpful to review typical radar and electronic warfare (EW) signal characteristics.
Radar systems are simple in concept, although often complex in function and implementation. They operate by transmitting short pulsed signals to “illuminate” or bounce off a target and then receive the signals that have been reflected by the target. Information from the radar returns can tell a great deal about a target, such as its distance from the radar’s transmit antenna, its relative size or radar cross section (RCS), and even its Doppler motion relative to the transmitted radar system.
Understanding Radar Signals
Carrier frequencies used in radar systems cover most of the usable radio-frequency (RF) spectrum, from the low frequencies used in long range and over-the-horizon (OTH) surveillance radar systems to the shorter millimeter-wave signals used in high-resolution military and civilian radars. Most radar systems operate below Ku-band frequencies (below 18 GHz).
Radar systems operate according to the radar range equation, which can be written in various forms. In one of the most common formats, the maximum detection range of a radar, Rmax, is defined according to
Rmax = {(PtG2λ2σ)/[(4π)3Pmin]}0.25
where
Pt = the transmit power;
Pmin = the minimum detectable signal;
G = the gain of the antenna;
λ = the transmit wavelength; and
σ = the radar cross section (RCS) of the target;
While this depiction of the radar range equation provides only a rough idea (no units of measure) of how the concept of reflected signal frequencies can provide information about an illuminated target, it offers an idea of how the different variables—such as transmit frequency and power and target RCS—contribute to the operation and performance of a radar. The radar range equation implies that the detection range is maximized as power increases, while spatial resolution improves as radar pulses become narrower. Since these two requirements are contradictory, pulse-compression techniques are often used to achieve optimized performance.
Radar signal characteristics can be described by two broad categories: pulsed RF and continuous-wave (CW) signals. In pulsed RF operation, the signal consists of periodic bursts of an RF carrier, which may or may not be modulated in terms of one or more signal characteristics, such as amplitude modulation (AM), frequency modulation (FM), or phase modulation (PM). The rate at which the pulses is generated is referred to as the pulse repetition frequency (PRF), while the period at which the pulses is generated is called the pulse repetition interval (PRI).
In CW radars, the RF signal is continuous and the range of the radar system is established through time markers carried on by a transmitted signal. The use of FM is the typical way to measure distance to target, since the instantaneous frequency detected from an illuminated target is dependent upon distance.
For pulsed RF radars, transmissions may be fixed or variable in frequency, using various frequency-hopping patterns. These patterns are complex by design, meant to be repeating by nature and difficult to predict. The carrier frequency may also change for each transmitted pulse. Some of the reasons that designers vary PRF over time are as follows:
- Echo ambiguity: Unambiguous ranging of targets is limited by the PRI, and targets located beyond that distance can be mistakenly positioned. One way to identify this behavior is to change the timing of consecutive pulses such that their position relative to nearby pulses will change.
- Doppler dilemma: The physics of the Doppler effect produce “blind speeds” for specific target velocities. Changing the PRF can change the location of blind speeds and detect previously unseen targets. Some radar systems switch between a high PRF optimized to obtain blind speeds greater than the expected target velocities and a slower PRF optimized for increased range.
- Protection against jamming: Variable PRI, often combined with complex stagger sequences, allows easier differentiation of signal echoes across radar systems. Some stagger sequences are also designed to confuse jammers based on digital-signal-processing (DSP) techniques.
Pulse compression techniques can increase the range of a radar system by transmitting longer pulses for increased average power. Echo processing at the receiver can deliver much better spatial resolution by “compressing” the pulse through correlation or dispersion processing. The two main pulse compression methodologies are as follows:
- FM chirp, which consists of fast frequency sweeps that can be linear frequency modulation (LFM) or nonlinear frequency modulation (NLFM). NLFM has some advantages compared to LFM in terms of efficient use of bandwidth, signal sensitivity, and receiver noise levels.
- Phase modulation, in which each pulse is composed of a series of shorter pulses where the carrier phase is controlled by a low-autocorrelation binary sequence of symbols. In binary-phase-coding modulation, the carrier phase changes between 0 and 180 deg. Polyphase pulse compression applies the same basic idea of changing phase, but the carrier phase is switched among more than simply two phase states.
Carrier phase coherence is an important issue for certain radar systems. In certain radar systems, such as high-performance coherent moving-target-indication (MTI) radar systems—where the phase of each pulse provides details about the precise position of a moving target—the phase coherence between consecutive pulses must be preserved to ensure precise positioning of the target.
Radar receivers detect target echo signals consisting of multiple superimposed signals returning from the same target. Some of the relative phase differences may be due to different signal reflections, different multipath signal delays, and different Doppler-related signal clutter and frequency shifts. While the transmitted signal may exhibit complex timing and modulation, the reflected signal will be much more complex due to environmental effects.
Generating Radar Signals
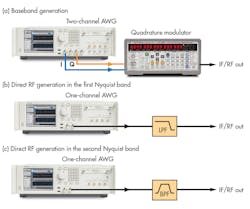
As Fig. 1 shows, AWGs can generate radar signals using three different basic methods: baseband generation, intermediate-frequency (IF) signal generation, and direct RF signal generation. When creating radar signals through baseband generation, an AWG generates a time-domain signal to be applied to an RF modulator. For simple signals, a single-channel AWG output is applied to an amplitude modulator (AM).
For more complex signals with complex forms of digital modulation or fast frequency sweeps (FM chirp), both the amplitude and the phase of the carrier must be instantaneously controlled. In such a case, the easiest and most flexible solution is a quadrature modulator with two baseband signals.
When creating radar signals by means of IF generation, an AWG generates a modulated signal at a relatively low carrier frequency. Often the signal can be applied directly to a signal-processing function block in the receiver or transmitter. In situations involving the final RF/microwave frequency, a frequency upconverter block may be needed to achieve the final required carrier frequency.
When creating radar signals by means of the final method, through direct RF/microwave generation, an AWG generates the modulated carrier at the final RF/microwave frequency. No additional signal-processing blocks aside from the expected filters and amplifiers are required to achieve the required radar signals.
Each radar signal generation approach has benefits and shortcomings. For most baseband and IF signals, an AWG with a sample rate of a few gigasamples per second (GSamples/s) is sufficient to achieve the required output frequencies. However, the modulation bandwidth of the final RF/microwave signal will be limited by the modulator or frequency upconverter.
In addition, wideband quadrature modulation is sensitive in in-phase/quadrature (I/Q) amplitude and phase imbalance or quadrature errors. Accurate alignment after a careful calibration is required to produce signals of sufficient quality using the baseband or IF radar signal generation approach.
Direct signal generation requires an extremely fast AWG with a sample rate at least 2.5 times higher than the maximum frequency component of the signal to be generated. These speeds are now possible with the latest generation of AWGs that can deliver quality signal generation beyond Ku-band frequencies (12 to 18 GHz).
An AWG can generate both undistorted or intentionally distorted signals according to their programming. The use of intentional distortion can compensate for distortion caused by external effects or components (such as connectors, cables, and other components) and can be used, for example, to improve amplitude flatness or group delay of a test setup.
Such compensation takes the form of a pre-emphasis filter to correct the signal-generation system’s overall lowpass frequency response. As high-frequency components are boosted, the low-frequency components of the signal must be attenuated to maintain a peak-to-peak value that fits within the available DAC dynamic range.
An AWG’s maximum sampling rate greatly influences signal quality. It is good practice to set the AWG sampling rate well above the minimum Nyquist requirement for generating a given signal frequency. Such oversampling increases signal quality in various ways, including providing flatter frequency response, greater image rejection, lower quantization noise, and lower pulse-to-pulse jitter. In fact, the main drawback to oversampling is the need for more memory – a reason why long record lengths are important to high-speed AWGs.
Generating test signals that closely resemble radar system signals can provide a tremendous boost when designing a radar system. For example, when one of the subsystems of a radar system is being designed, the remaining parts of the system are often unavailable for testing. By using off-the-shelf, general-purpose test equipment to simulate other subsystems within the full system, the device under test (DUT) can be tested under controlled signal conditions.
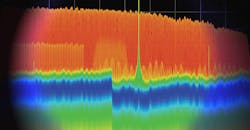
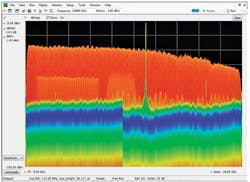
A test signal source capable of generating signals that closely match the signals that will be used by an actual radar system provides the means of characterizing that system under actual operating conditions. A wideband AWG, for example, can be used to simulate a cluttered open-air signal environment, as represented by Fig. 2.
The signal environment includes wide- and narrowband chip signals, narrowband signals, CW signals, and frequency-hopped radar signals, all captured by a real-time spectrum analyzer. Several communication signals and other interferers can also be seen in the same frequency bands as the radar signals.
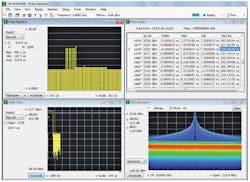
Radar transmitter testing includes extensive evaluation of a wide variety of test signals. In many cases, the evaluation involves hundreds or thousands of pulses that are then analyzed using statistical techniques. As an example, Fig. 3 evaluates the PRI on a set of 2,000 pulses constructed as a staggered PRI CW pulse waveform using a high-speed AWG. The histogram provides a statistical view of the distribution of the PRI measurements, while the pulse table and pulse waveform can be used to view measurements for each pulse.
Direct Carrier Generation
An ideal AWG can generate output signals from DC to within one-half the sampling rate. Given a sufficiently high sampling rate, an AWG can directly generate a modulated RF/microwave test signal. Prior to current-generation AWGs, available AWGs suffered from relatively low sampling rates and poor spurious-free dynamic range (SFDR), which limited the generation of output signals for radar tested to a few GHz.
Direct signal generation with an AWG offers several advantages over traditional baseband/external modulator signal generation approaches. Among them:
- Baseband generation and quadrature modulation are performed mathematically;
- No additional equipment is required;
- A single AWG can generate multiple dissimilar carriers or wideband noise so that more realistic test scenarios can be provided by a single instrument; and
- Direct signal generation can be achieved using a simplified calibration procedure.
Although these advantages are significant, actual implementations of this architecture can reveal some drawbacks as well. One important issue is record length requirements. For a given record length, RL, the maximum time window, TW, that can be implemented is inversely proportional to the sampling frequency, fs, or TW = RL/fs.
Since sampling rates for direct RF generation must be higher than those for baseband signal generation, a given record length translates into a shorter TW for direct RF generation than for baseband signal generation. The RL is crucial for realistic emulation of complex radar systems incorporating staggered pulse sequences, frequency-hopping patterns, or time-varying echo characteristics caused by target movement or antenna vibration.
Generation of wideband signals may require the controlled addition of linear distortion to correct for amplitude flatness problems and phase linearity issues, such as those stemming from coaxial cables and connectors. Applying corrections based only on the amplitude response improves modulation quality performance, although phase response compensation is also required for optimal performance. Direct carrier generation also requires excellent sampling clock jitter performance because this translates directly to phase noise in the generated carriers.
Some applications, such as MIMO radar generation, require multiple test signal channels. The channels must also be synchronized, so they must share the same sampling clock and be time-aligned. Any timing difference among channels or channel-to-channel jitter will result in a reduced-quality radar test signal. When more than one instrument must be synchronized, standardized synchronization methodologies can simplify the alignment tasks while dramatically improving repeatability and reliability.
Continuous signal generation with an AWG is made possible by seamlessly cycling the contents of the waveform memory through the DAC. To obtain useful signals, consistency of the signal around the wrap-around event must be preserved. Timing characteristics of radar signals are especially important for the following reasons:
- PRI: An integer number of PRIs must be stored in the waveform memory. Otherwise abnormal pulse timing (longer or shorter than required) will occur every time the waveform is cycled.
- Carrier phase: For coherent radar emulation, carrier phase must be preserved. This condition can be met if record length and sampling rate are selected so that the resulting time window is an exact multiple of the carrier frequency period.
- Echo consistency: Multipath, filtering effects, and echoes beyond the unambiguous range must propagate from the end of one cycle to the next. The previous effects are seen as the convolution between the transmitted signal and the target system impulse response. Applying circular convolution to a consistent transmitted data set will create an echo emulation signal without any discontinuity or abnormal behavior.
In short, the latest AWGs allow for the direct generation of complex radar signals to carrier signals as high as 20 GHz in frequency. Such performance capabilities are made possible by recent breakthroughs in DAC technology and DAC components. Even the most complex frequency-agile or MIMO radar systems can now be emulated through direct RF/microwave generation—either coupled with deep waveform memory and time alignment between channels within a single signal generator, or else by means of multiple synchronized sources.