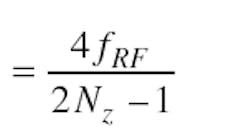High-speed analog-to-digital converters (ADCs) have changed most approaches to receiver front ends. An ADC allows a good portion of the analog signal chain leading from the antenna to be eliminated. Similarly, in an instrumentation system, a high-speed ADC allows signals from a sensor to be quickly digitized with a minimum of analog processing. To demonstrate effective practices in directly digitizing RF signals, the RF subsystem for an instrumentation product used in high-energy physics will be examined. The instrument, which consists of an RF chain and a digitizer, can directly process and sample RF signals to 500 MHz. Although it is only one subsystem, it plays a crucial role for the final system since it defines the limitations of the test instrument.
The RF subsystem has several demanding performance requirements, including high signal-to-noise ratio (SNR) and good linearity. To achieve these requirements, an investigation was launched into digitizer performance limitations imposed by noise. A mathematical model for the system's noise sources was developed in order to predict output SNR and compare this to actual measurements. Figure 1 shows a simplified block diagram of the RF subsystem.
When sampling high-frequency signals, it is necessary to fulfill two criteria in order to avoid aliased components. The first criterion demands that the bandwidth of the signal to be sampled should not exceed one half of the sampling rate, or fs/2. To fulfill the second criterion, the maximum and minimum frequencies of the sampled signal should be within the same Nyquist zone. Equation 1 can be derived by using both criteria:
where:
NZ = the Nyquist zone number, and
fRF = the center frequency of an arbitrary RF input signal.
If the signal with center frequency fRF and bandwidth not exceeding fs/2 lies in the first Nyquist zone (NZ = 1), then a sampling frequency of fS = 4fRF is optimal. But under such conditions, modern ADCs would not allow sampling of signals with center frequencies higher than a few hundreds of MHz. Still, this limitation can be overcome if the Nyquist zone number is properly chosen. As seen from Eq. 1, increasing NZ means that a high-frequency RF signal can be sampled with a relatively low sampling frequency, an approach known as under-sampling. For example, sampling an arbitrary signal with center frequency fRF = 500 MHz, bandwidth of fS/2, and Nyquist zone of NZ = 9 requires a sampling frequency of fS = 117 MHz.
An AD9433 ADC from Analog-Devices (www.analog.com) was selected for the RF subsystem. It is specified with a maximum sampling frequency of 125 MHz and therefore fulfills the need for a high sampling frequency of fS = 117 MHz. Figure 2 shows the spectrum of an arbitrary signal and the frequency translation effect of the under-sampling technique.
A major problem of the under-sampling technique is the additional components that appear outside the signal bandwidth of interest. In order to limit the signal bandwidth to less than fS/2, an anti-aliasing bandpass filter was added to the RF chain. The anti-aliasing filter has an 8-MHz bandwidth, a center frequency of 498 MHz, and passband insertion loss of 3.5 dB. It is a surface-acoustic-wave (SAW) bandpass component with more than 50-dB suppression of signals outside the chosen Nyquist zone. It is located at the input of the RF subsystem to suppress unwanted frequency components that would otherwise be amplified in the RF chain.
One of the functions of the RF signal chain is to keep the amplitude at the input of the ADC constant whenever the input signal is within the specified dynamic range, requiring high gain and programmable gain control. The RF chain developed for the instrumentation product features four amplifiers with gain of about 20 dB. Two variable attenuators with maximum attenuation of 31 dB and 1-dB steps each facilitate programmable gain control.
When designing the RF subsystem, some generic rules were followed. The first amplifier was chosen to be a lownoise amplifier with considerable gain to set the noise figure of the system. Similarly, the last amplifier has the highest third-order intercept point in order to set the dynamic range of the amplifying chain. A lowpass filter is placed between to prevent out-of-band oscillations. At the end of the RF chain, another SAW bandpass filter is used to eliminate unwanted frequency components possibly generated by the RF chain. A 3-dB attenuator in front of each SAW bandpass filter improves the filter's return loss (S11).
Once the topology of the RF chain is set, its basic limitations can be studied. For high-level input signals, nonlinearity is a major problem. The variable attenuators must be properly set to achieve good linearity performance in the RF chain. The ADC's linearity is measured by comparing two signals coming from the same analog source and sampled on the same ADC, but one passed through a 6-dB attenuator before being sampled. Figure 3 shows the ADC's decibels full scale (dBFS) as a function of the input signal power for both signals and the ratio between them. In Fig. 3, it can be seen that the ADC at high power input levels has a nonlinearity of 0.1 dB per 15-dB change of input signal power, which cannot be neglected for a wide dynamic range. Maintaining signals to the ADC at a constant input level would solve the problem. For the RF subsystem, the input level to the ADC was maintained at about -5 dBm, for a tradeoff between RF chain and ADC linearity levels.
Page Title
At low-level input signals, the performance of the system is limited by noise. To study these limitations, a model of major noise sources was developed. The model consists of mathematical equations that describe the behavior of the noise, depending upon a specific parameter for each noise source. There are three major noise sources in the system: the RF chain as a thermal noise source described by the RF chain's noise figure; the ADC as a quantization noise source described with the number of ADC bits; and the clock generator as a phase-noise source described by the clock root-mean-square (RMS) jitter.
The RF chain is mainly a thermal noise source. The SNR at the output of the RF chain is defined as the input SNR reduced by the noise figure of the RF chain. The noise figure of the RF chain is a function of the equivalent noise temperature as seen in Eq. 2:
where:
kB = Boltzman's constant B = the bandwidth of the measured noise,
TO = room temperature at the input of the RF chain, and
G(Pin) = the gain of the RF chain, which is a function of the input signal power, Pin.
The equivalent noise temperature, TeqRF, of the RF chain has to be derived for the topology described above by using equivalent noise temperature and gains for each stage. The noise power at the output of the RF chain is defined by Eq. 3:
The function G(Pin) increases linearly-when the input signal power is decreasing. The noise figure (NF) of the RF chain depends on the input signal power or variable attenuator values, and it varies from 19 dB at low-level input signals to 31 dB at high-level input signals. The RF chain is for an instrumentation device with tight requirements regarding linearity, and such a high noise figure is acceptable due to the relatively high input signal power, which guarantees high SNR at the output of the system.
Besides nonlinearity and aliasing problems, ADCs add quantization noise to the signal. Assuming that the AD9433 has a linear quantization scheme and that the probability distribution of the quantization error is constant, it is possible to derive Eq. 4 to solve for output SNR.
where:
N = the number of bits used (12 b for the AD9433);
Δ= the voltage per single quantization step;
K = the ratio between actual amplitude and full-scale amplitude;
VFS = the full-scale amplitude of the ADC; and e = the random variable of quantization error (in V).
The logarithmic value of Eq. 5 yields the SNR at the output of an ADC.
Ratio K decreases the SNR at the output of the ADC. The value of factor K is defined after the most linear region of the ADC is measured and consequently the input signal power to the ADC is determined. In the case of the AD9433, the SNR is 15 dB lower than full scale. Equation 6 shows the quantization noise power added to the signal by the ADC. The quantization noise power level is not a function of input signal power.
Page Title
For the sampling clock source, the major degrading factor is phase noise. Sampling causes phase-noise characteristics to transform in an exact shape around fRF- 4fS. Comparing white Gaussian flat noise with phase noise, which has a f-1 shape, is simpler when including the concept of jitter. Instead of phase noise, which is a narrowband parameter, sampling clock uncertainty can be expressed in terms of RMS jitter, which is a broadband parameter. Equation 7 shows the connection between phase noise and RMS jitter.
where:
L(f) = the ratio between the phase noise power level and the signal power level at a frequency offset f from carrier fS.
For the crystal-oscillator sampling clock source used in the RF chain, its phase noise can be measured with a spectrum analyzer or pulled from the data sheets for the oscillator. The nearest measured ratio for the case of the oscillator used in the RF chain is -73 dBc/Hz at a offset frequency of 10 Hz, which is also the highest measured ratio. The lowest specified phase noise for the sampling clock source used in the RF chain is -137 dBc/Hz. The RMS jitter as defined in Eq. 7 increases the noise power level over the Nyquist zone when a signal with frequency fRF is sampled. The SNR is defined in Eq. 8.
Equation 8 is a worst-case equation because it supposes that sampling occurs at a zero crossing where the slow rate is at its maximum. The noise level produced by the clock's phase noise is a function of the input power to the ADC, as shown in Eq. 9.
The total theoretical noise power at the output of the mathematical model is the sum of all three noises, as shown in Eq. 10
Figure 4 shows the noise power levels of all noise sources at different input power levels, calculated using Eqs. 2 to 10. The thermal noise contribution to the overall noise increases as the input signal decreases. The lowest thermal noise of the RF chain is defined mainly by the high value of attenuation combined with the first three amplifiers in the amplifying chain. At low input power levels, the noise power level is a linear function of input signal power. Summation of the three noise sources shows that at high-level input signals, the noise level of the RF chain and digitizer is defined mainly by the phase noise and is -122 dBm/Hz (Fig. 4). This is also the theoretical minimum for the noise power at the output of the RF chain and digitizer. At low-level input signals, the sum of the three noise sources is dominated by the thermal noise of the RF chain, which increases the overall noise power level to its highest value, -102 dBm/Hz. Quantization noise does not play a significant role in the modeling of noise sources because it is too low in comparison to thermal noise of the RF chain and the phase noise.
It is worth noting that even if the resolution of the ADC were 10 b instead of 12 b, it would still not influence the noise summation considerably. To prove the reliability of the mathematical model described here, measurements of noise power level at the output of the RF chain and digitizer were performed. Data from 32k samples were acquired using a logic analyzer, and the noise power level was measured at bandwidths defined by the input bandpass SAW filter. Figure 5 shows the Fast Fourier Transform (FFT) of a CW 500-MHz signal with -5 dBm power at the output of the RF chain. The scale of the FFT is set to dBFS in order to calculate the absolute noise power level at the output of the system.
The results of repeating the measurements at different input power levels are shown in Fig. 6, which plots noise power at the output of the system as a function of input power. The modeled results fit measured values within a 2-dB window.
Modern ADCs make it possible to build digital receivers to 500 MHz based on direct sampling of RF signals. The so called under-sampling design approach is replacing mixer-based heterodyne receivers. Measurements shown in this article demonstrate that with proper but simple RF signal chains, many potential limiting factors can be avoided. The noise power level due to sampling clock jitter is the major limiting factor and it defines the SNR of the system for high-level input signals. By proper selection of clock sources, clock distribution circuits, and proper layout design, clock jitter can be minimized to allow the use of the under-sampling technique for digitizing RF signals through 500 MHz.
REFERENCES
- Boris Drakhis, "Calculate Oscillator Jitter by Using Phase-Noise Analysis," Microwaves & RF, February 2001, pp. 109-119.
- Jeffrey H. Reed, Software RadioA Modern Approach to Radio Engineering, Prentice-Hall PTR, Englewood Cliffs, NJ, 2002.
- Joseph Mitola, Object-Oriented Approaches to Wireless Systems Engineering, Wiley, New York, 2000.