Carrier Modifications Make Ultranarrowband Modulation
Download this article as a .PDF
Wireless systems and services occupy bandwidth, which is limited. But not all wireless applications require wide-bandwidth channels. Emerging applications such as sensors for Internet of Things (IoT) functions need just enough bandwidth to move the amount of data generated by the sensor to a communications gateway that is connected to the internet.
For industrial and commercial applications such as these, ultranarrowband (UNB) wireless technology is very attractive as a means of providing a wireless link without occupying a great deal of frequency spectrum. One of the challenges in adopting UNB technology, however, lies in generating the necessary signals—essentially carriers without sidebands.
In modern communications systems, modulated carrier signals occupy fairly wide-bandwidth channels to transfer voice, video, and data. Because of the wide-bandwidth channels, including sidebands, channels must be sufficiently separated in frequency to avoid overlapping sidebands and causes of interference between channels. But UNB-modulated channels, which theoretically have no sidebands and can compress large amounts of data into communications channels as narrow as 1 Hz or less, can be closely spaced while still occupying very little total frequency spectrum.
Of course, UNB-modulated signals must be generated before they can be used in practical applications. For the past 20 years, perhaps a dozen different methods have been proposed for generating UNB signals. In comparing the methods, it becomes apparent that all have a common trait of modifying the carrier signal in some way. As Lee pointed out,1 one goal in the use of any modulation format was to achieve as little distortion as possible on the carrier waveform, since an undistorted continuous-wave (CW) carrier requires 1 Hz or less filter bandwidth to deliver the modulation information.
As an example, assume a carrier signal that is modified by changing frequency and a narrowband filter (with passband of 1 to 2 kHz wide). The modifications to the carrier causes a “breakout” that leaves a hole or space in the signal (missing cycles or portions of cycles) that appears at the output of the filter (Fig. 1). All UNB modulation methods experience such breakouts.2 A carrier signal can be modified by changes in amplitude or phase. In either case, the signal that is being transmitted consists of the fixed-frequency carrier along with some very low-level sin(x)/x sidebands.
The addition of some form of modulation, whether based on changes in amplitude or frequency/phase, is obvious for a waveform where the carrier is being stretched, causing the carrier to be at a lower frequency during the bit change. For a modulation method that uses 90-deg. changes in phase, the carrier cycles will be stretched by 90 and 270 deg., lowering the carrier frequency at those points and causing a breakout at the data-transition edges (Fig. 2). In a case of missing cycles with amplitude modulation (AM), the change in carrier cycles is 360 deg.
For other UNB modulation methods, the carrier signal must have the DC component of the breakout event restored (Fig. 3). A limiter cannot be used for this purpose, and the modulation circuitry must exhibit a nonlinear response in order to achieve the UNB modulation. Restoring the DC component in such as case is difficult for a system that must provide a large dynamic range.
The sin(x)/x level of the system must be proportional to the phase angle of the carrier modification or width of the carrier breakout. Thus, 90 to 270 deg. for the 90-deg. phase method has lower sin(x)/x sidebands than the sidebands resulting from the 360-deg. breakout for a missing carrier cycle.
Carrier breakouts can be used in various ways as part of an approach to producing UNB modulation. Breakouts can be used to mark the presence of a digital one, digital zero, or both, according to the carrier modification method that is chosen. The sin(x)/x sidebands which are the AM that results from the carrier modifications can be removed further by filtering, which has no effect on the phase angles or how the breakouts are used to convey digital information.
For 90-deg. phase modulation of the carrier, data is between carrier modification points (Fig. 4), so a limiter can be used to achieve the modulation since it ignores the amplitude of the carrier modification points.3,4 A 90-deg. phase modulation angle is optimum; for smaller angles, the sin(x)/x sideband shoulders are reduced by as much as 3 dB, but the bit error rate (BER) is worse.
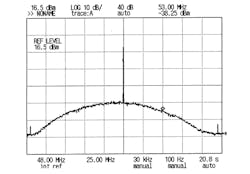
For angles greater than 90 deg., the BER remains the same but the sin(x)/x shoulder reduction is not as great. Figure 5 shows the UNB spectrum for a data rate of 12 Mb/s with a 48-MHz intermediate frequency (IF) and applies to all methods used to create UNB modulation.
Communications channels that employ this carrier breakout approach to transfer data can be located very close in frequency to one another. Testing on UNB channels spaced only 10 kHz apart has shown successful reception of transmitted data, regardless of data rate.5 In these tests, performed with specialized filters, the modulated signal sidebands were not required as part of the transmissions. Such closely spaced UNB-modulated carriers meet most FCC requirements for radiated signals.
The filters used in this testing are known as negative-group-delay filter or zero-group-delay filters.6 If such filters are not used, the modified carrier cycle will be smoothed over (by filters with positive group delay) and lost (along with any data represented). Conventional bandpass filters (BPFs) exhibit positive group delay, which means they integrate and smooth over input signals.
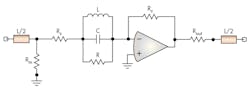
Unfortunately, negative-group-delay filters are not covered in any engineering textbooks, although information on such filters is available on the internet. Some of the types of negative-group-delay filters that have been used to achieve UNB modulation include the Walker shunt filter, the transformer reflected shunt filter, the series emitter filter with feedback,6 and the wavelet filter. A series emitter filter with positive feedback is a quality factor (Q) multiplier circuit where gain is controlled by a discrete resistor.
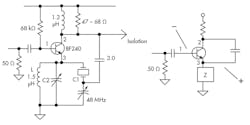
Negative-group-delay filters should more accurately be referred to as zero-group-delay filters. True negative-group-delay operation is not possible, since it implies negative time. Filters with zero group delay are possible, and they can be realized using L and C components or with crystal resonators (Figs. 6 and 7). LC filters are generally not recommended for UNB applications, since they tend to have poor shoulder reduction and broader bandpass characteristics than crystal filters.
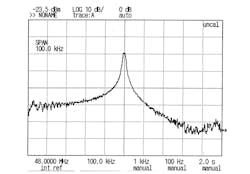
Figure 8 shows the spectrum of a phase-modulated signal following one stage of a zero-group-delay BPF. There are no sidebands and the sin(x)/x pattern is removed, thus there are no contributions to the carrier phase shift or amplitude molestation. Figure 9 is the bandpass response of a crystal filter with zero group delay. The 3-dB bandwidth is about 500 Hz for a 48-MHz intermediate frequency (IF). Any sidebands, such as the sin(x)/x AM pattern, are reduced by approximately 30 to 40 dB.
Error Probability
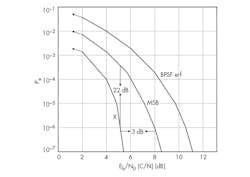
In Fig. 10, the curve on the right shows binary-phase-shift-keying (BPSK) modulation, which is being used here as a reference for comparison. By using UNB modulation, the carrier-to-noise ratio (C/N) is improved by about 3 dB. This dramatic improvement has been measured by a number of researchers, including those at xG Technology and UNBTech. The improvement is shown in the minimum-sideband (MSB) curve, for which the filter bandwidth is assumed to be equal to the data rate (no additional filter bandwidth is needed for removal of sidebands).7
A reduction in noise power is generally beneficial to the performance of any communications system. The noise power, Pn, is given by Pn = kTB, where k is Boltzmann’s constant (1.38 × 10-23 J/K); T is temperature (in ºK); and B is bandwidth (in Hz). Such a reduction is possible if the bandwidth of the negative-group-delay filter is equal to or less than the bit rate.
For example, a communications system transmitting data at 12 Mb/s using binary-phase-shift-keying (BPSK) modulation uses a filter bandwidth of 12 MHz. However, by using MSB or one of the UNB phase-modulation methods described earlier, and the crystal filter of Fig. 7, the resulting noise bandwidth is only about 500 MHz, following the probability of error (Pe) calculations detailed in Eq. 1:
Pe = 0.5erf(X) = 0.5erf(Eb/N0)0.5
= 0.5erf{[(signal power)(noise power)]/[(bit rate)(bandwidth)]} (1)
As Eq. 2 shows, this is a noise-bandwidth reduction of 12,000,000/500 or 24,000:
X = [(signal energy/bit rate)/(noise energy/12,000,000)]0.5 →
[(signal energy/bit rate)/(noise energy/500)]0.5
= (24,000)0.5 = 154.91933 (2)
The error probability decreases as the noise power decreases with decreasing filter bandwidth. The carrier-to-noise (C/N) ratio becomes smaller, moving the curve for X in Fig. 10 toward the left.
In applying Eq. 2, it can be seen that changing from a 12-MHz filter bandwidth to a 500-Hz filter bandwidth results in a dramatic improvement in C/N ratio and an increase in X of almost 155 or 22 dB. This can be seen plotted as the line marked by “X” at the left of the MSB curve in Fig. 10. The Pe has been improved by 22 dB. Also, the C/N ratio required to produce a given bit error rate (BER) is lowered by approximately an additional 3 dB, which represents a significant improvement in the C/N ratio. Alternately, signal power can be reduced by 3 dB (Eq. 1), keeping the C/N ratio and the MSB curve the same, as X varies with the C/N ratio.
UNB methods offer a distinct performance advantage compared to BPSK modulation, which is often used as a reference for digital data communications. UNB provides a 6-dB improvement over the BER performance possible at the theoretical limits of BPSK and 8 dB better than differentially encoded BPSK. In fact, since the data rate, filter frequency, and bandwidth are independent, the data rate can be varied with UNB or frequency modulated (FM) to modulate a UNB signal with audio.
References
1. William C.Y. Lee, Lee’s Essentials of Wireless Communications, McGraw-Hill, New York, 2001.
2. Shikai Zhang, “Assessing Different Ultra Narrowband Formats,” Microwaves & RF, August 2012, p. 78.
3. H.R. Walker, “Experiments in Pulse Communications with Filtered Sidebands,” High Frequency Electronics, September 2010, pp. 64-68, www.highfrequencyelectronics.com.
4. H.R. Walker, “Sidebands are not Necessary,” Microwaves & RF, August 2011, p. 72.
5. Shikai Zhang, “Compressed UNB-OFDM Delivers High Data Rates,” Microwaves & RF, January 2016, p. 48.
6. H.R. Walker, “Making the Most of Ultranarrowband Modulation,” Microwaves & RF, July 2015, p. 56.
7. Shikai Zhang, “UNB Modulation Salvages Spectrum,” Microwaves & RF, posted April 15, 2009.