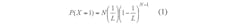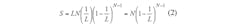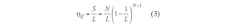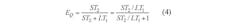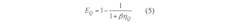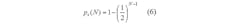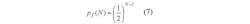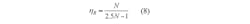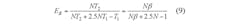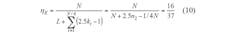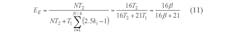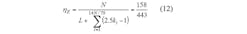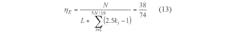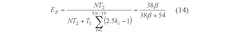Algorithm Aids RFID Anti-Collision Success

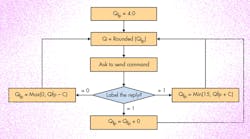
Figure 1 shows the method for the Q algorithm to adjust the frame length. The algorithm defines a floating number, Q_fp, and a constant, C, with typical value of C being 0.1 < C < 0.5. Based on a current slot state, the Q algorithm updates the Q_fp value adaptively, and Q_fp is rounded down to an integer value, Q. When the current slot collision occurs, Q_fp increases C; when the current slot is idle, Q_fp decreases C; and when the current slot successfully identifies a tag, Q_fp remains unchanged, as in the algorithm flow chart of Fig. 1.

Assuming a frame length of L in the Q algorithm, the total number of tag(s) is represented as N and the probability of M tag(s) in a slot is subject to a binomial distribution. The probability of recognition, which is the probability that only one tag exists in a slot, is depicted by Eq. 1:

Since L slot(s) exists in one frame, the number of tag(s) that can be identified in a frame is found by means of Eq. 2:

The throughput rate of the Q algorithm, η_Q, can be found by Eq. 3:

If T₁ represents the time for collision detection of tags, and T₂ is the time required to successfully identify a tag, the recognition efficiency of the Q algorithm, E_Q, can be found by means of Eq. 4:

In the case where β = T₂/T₁, due to η_Q = S/L,

In the Q algorithm, the frame length can be quickly adjusted to an optimum length by modifying the Q value.⁶ Also, E_Q has been greatly promoted in the Q algorithm compared to the RFID dynamic frame slot algorithm (DFSA).⁷  However, to achieve an optimal frame length using the Q algorithm, the Q value must be frequently adjusted, which increases the amount of communication required between reader and tags. Meanwhile, the reader randomly selects values each time, consuming system resources and reducing E_Q. An evaluation of different RFID anti-collision algorithms may serve to help enhance the Q algorithm.

In a binary tree (BT) anti-collision algorithm,^8-11 for example, each tag has a counter and a random number generator that can generate 0 or 1. At the beginning, the counter value of each tag is 0 and the tag card is in the waiting state. When a reader sends a query command, the tag with the counter showing 0 responds. When two tags collide, the one showing 0 is randomly added with 0 or 1. As a result, the tags on collision bits are classified into two sub trees, and the tag which counter does not show 0 is directly added with 1.

If no collision is detected by the reader, the counter values of all tags subtract 1. Whether or not it is 0 is then determined, so as to decide whether the tags are to respond to the reader or continue to wait. Such loop detection continues until all tags are identified. In the event that the random values generated by the tags are always 1 for a given period of time, the tags will remain in a waiting state and not be recognized. Therefore, the BT algorithm is a possible solution for use as an RFID anti-collision algorithm. Where there are few RFID tags, the recognition efficiency of the BT algorithm is not very high. But where the number of tags is large, it has a high recognition speed.^12,13

The BT anti-collision algorithm dictates that when N tags collide, they are grouped by randomly selecting 0 and 1. As shown in Eqs. 6 and 7, the probability of the tags that can be separated is expressed as p_s(N), while the probability of tags that cannot be separated is expressed as p_f(N):^14-17

From these two equations, it can be seen that the larger the number of collided tags, N, the smaller the value of tags that cannot be separated, p_f(N), will be. In the case of N >> 2, the throughput rate, η_B of successfully identified N tahgs can be approximated by Eq. 8:

For the BT approach, the recognition efficiency, E_B, can be found by means of Eq. 9: 

Using the Q algorithm, tags can be quickly classified into different groups, and certain rules must be adopted to adjust the Q values to make the slot counts approximately equal to the number of tags to be identified. In this way, the throughput can reach a maximum rate. But if the collision resolution mechanism of the Q algorithm is ineffective, the recognition time will be extended if the Q value must be reselected.^18,19

Each tag has two counters, Ct1 and Ct2, in the RFID system. Counter Ct1 is used to save the random number selected by the tag, and counter Ct2 is used to back up this random number. It contains a counter (C_r) and queue (s_c) in the reader, with counter C_r (C_r = 2) used to save the Q value and determine whether a slot comes to an end. Queue s_c is used to save the random number selected by the collision slot. The nine related algorithm steps are as follows:

1. In the first step, the reader randomly selects one Q value and sends it to the tag to be identified, saving the value in C_r (C_r = 2^Q.

2. In the second step, after the tag has received one Q value, a value among 0 – 2^Q – 1 is selected randomly, then saved in Ct1; at the same time, this value is backed up in Ct2.

3. Next, the reader sends a query command and the Ct1 = 0 tag responds to it. If there is no tag response to the query command, a free slot is started. When more than one tag responds, there will be a collision slot, Ct1, of the collision tag is set to the maximum value; the Ct2 value is kept in the s_c queue. If only one tag responds, there will be an identification slot, during which the tag will be identified and marked as being in the identification state. 

4. In the fourth step, the reader counts C_r – 1, with the Ct1 of all other tags minus 1.

5. The fifth step is to determine whether C_r is zero. In the case where C_r ≠ 0, shift to step 3. In the case where C_r = 0, the first frame ends. In addition to the recognized tags, the collided tag Ct1 is set to the high position and Ct2 records the value initially randomly selected by each tag. The reader makes judgments based on the proportional relationship of the idle slot, the identification slot, and the collision slot in the frame. If meeting rule R1, the adjustment of Q ← Q – 1 is made, the queue s_c is emptied, and the process begins again with step 1. If rule R2 is not met, move to step 6.

6. In step 6, the reader sends a command, resulting in the tag’s Ct1 = Ct2.

7. The seventh step is to determine whether the reader queue, s_c, is empty. If empty, all tags have successfully identified in the first phase and it withdraws the identification process. If it is not empty, it is “dequeued” to C_r and sent a command to make the tag to be identified Ct1 ← Ct1 – C_r.

8. In the eighth step, the reader sends a query command and the Ct1 = 0 tag responds. If there is no tag response, an idle slot will result and the Ct1 for all tags will be Ct1 – 1 before repeating step 8. If multiple tags respond, a collision slot will result, with the Ct1 = 0 tag having 0 or 1 randomly added; in addition, the remaining tags will have 1 added to Ct1 before repeating step 8. If only one tag responds, there will be a recognition slot. This tag will be identified and marked in the identification state, with Ct1 – 1 assigned for the remaining tags.

9. In the final step, the reader will send a command, and the tag of counter Ct2 = C_r will respond. If multiple tags respond, there will be a collision slot. All tags will have Ct1 – 1, and a Ct1 = 0 tag will be randomly added after 0 or 1 before repeating step 8. If only one tag responds, there will be only a tag left in the collision slot to recognize the tag before going to step 7 to recognize the tag in the next collision slot.

Assuming N tags to be identified in the RFID system, the proportional relationship among N₀, N₁, and N_m can be classified into one of three conditions for analysis of the IAS algorithm. For the first condition, N₀: N₁:N_M = 1: 1: 2/3.

Under this proportional relationship, L = N, there are η₁ = (8/3)N tag(s) identified, and η₂ = (5/8)N tag(s) collided in the (1/4)L = (1/4)N slot to start the recognition segment. Setting the number of tags contained in the ith collision bit as k_i, the total number of tags identified can be expressed as:

η₂ = ∑^N/4_{i = 1}k_i

The total throughput of the IAS algorithm for this first condition can be found by Eq. 10:

The recognition efficiency of the IAS algorithm can be found by Eq. 11:

For the second condition, N₀: N₁: N_M = 2: 1: 7/24. In this proportional relationship, for the case of L = 2N, the tag η₁ = (48/79)N is identified and the tag η₂ = (31/79)N collides in the slot (7/79)L = (14/79)N. It then starts the identification phase of:

η₂ = ∑^(14/79)N_{i = 1}k_i

The total throughput of the IAS algorithm for this second condition can be found by Eq. 12:

For the third condition, N₀: N₁: N_M = 1: 2: 10/3. In this proportional relationship, in the case of L = N/2, the tag η = (6/19)N is identified and the tag η₂ = (13/19)N collides in the slot (10/19)L = (5/19)N. It then starts the identification phase where:

η₂ = ∑^(5/19)N_{i = 1}k_i

Therefore, for the third condition, the total throughput of the IAS algorithm can be found by Eq. 13:

In the event that L = N/2, the recognition efficiency of the IAS algorithm is given by Eq. 14:

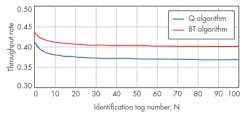
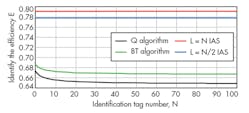
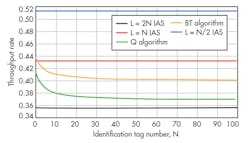
Figure 3 provides a comparison of the recognition efficiencies of the Q, BT, and IAS algorithms at β = 5. It shows that the IAS algorithm is superior to other two algorithms in recognition efficiency. Figure 4 indicates that in case of L = N/2, the IAS algorithm has a higher throughput but, due to β = 5, the time, T₂, required to successfully recognize a tag is five times the time T₁ for collision detection. Hence, the IAS algorithm has higher recognition efficiency in the case when L = N.

RFID systems have drawn upon different algorithms for operation. For example, tags can be quickly classified into different groups by means of the Q algorithm. By adjusting the Q value according to certain rules, and matching the number of slots with the number of tags to be identified, the Q algorithm can achieve high throughput. The BT algorithm is effective for solving the RFID tag collision problem.

By combining the benefits of these two approaches, the IAS algorithm can quickly group tags using the Q algorithm’s mechanisms while also minimizing collisions by means of the BT algorithm. But the IAS algorithm offers superior performance to the Q and BT algorithm approaches in terms of throughput, slot counts to recognize certain numbers of tags, as well as in recognition efficiency.

Acknowledgments

This work was financially supported by the Science Research Fund of Daqing Normal University (12ZR17). The authors would like to thank Daqing Normal University for providing the facilities and resources to perform this research. Also, the authors would like to thank our colleagues at the Department of Physics and Electrical Information Engineering of Daqing Normal University for their excellent collaboration and help during the preparation of this article.

Guihua Yang, Professor

Junchi Ma, Master

Yukai Gao, Master

Baohong Fu, Master

Chunmei Wu, Master

Department of Physics and Electrical Information Engineering, Daqing Normal University, Heilongjiang, 163712, People’s Republic of China