Stability can be difficult to achieve in microwave circuits with gain (nonlinear behavior), such as amplifiers and oscillators. Amplifier designers, for example, have long dreaded the appearance of oscillations in a carefully considered circuit. When that circuit is in monolithic-microwave-integrated-circuit (MMIC) form, a "fix" requires another foundry run.
But help in achieving microwave circuit stability has arrived, by way of the stability analysis (STAN) software developed by AMCAD Engineering (www.amcad-engineering.fr) and sold by Maury Microwave Corp. (www.maurymw.com). The tool, which works with a commercial computer-aided-engineering (CAE) simulation platform—such as the Advanced Design System (ADS) from Agilent Technologies (www.agilent.com) or Microwave Office from AWR (www.awrcorp.com)—is based on a stability analysis technique that can locate and characterize the unwanted oscillations in power amplifiers (PAs) that are evidence of instability. The stability analysis tool helps RF/microwave engineers develop networks that improve circuit stability without sacrificing the performance goals of the original circuit design.
Modeling tools like STAN are supported by device characterization capabilities, as provided by AMCAD and Maury Microwave (www.maurymw.com) with their load-pull test systems. Device stability or instability is often expressed in terms of the Rollett stability factor, K, or the Linville stability factor, μ. Graphically, they are often shown in terms of the distance from the center of a Smith chart to points on an input or output stability circle, representing input or output networks where instabilities may lie. Spurious oscillations arise from feedback loops, and can start with device bias (the linear or small-signal stability of the circuit) or the dynamic power applied to the circuit (the nonlinear or large-signal stability).
It is in a designer’s best interest to understand the nature of these oscillations early in the design process. Various methods are available to analyze the small- and large-signal stability of a microwave circuit. Some of these approaches have been incorporated in commercial CAE simulators for use with simple linear two-port networks, and are not really suitable for multiple-device networks such as amplifiers.1 Some small-signal analyses have been presented in the literature,2,3 but these are difficult to apply to circuits with a large number of active devices. While the stability envelope approach4 has been implemented in a commercial CAE simulator, it can be difficult to determine the origin of an instability and its start-up frequency.
Commercial CAE simulators typically lack the capability to perform large-signal steady-state stability analysis. A number of approaches have been developed for microwave circuits,5-10 but they either lack reliability or are too complex for practical use with current processing hardware. For example, the nonlinear normalized determinant function (NDF) technique6 is time consuming to implement and requires access to the intrinsic nodes of the models for transistors used in an amplifier undergoing analysis. Simplified versions of the NDF approach are easier to apply but may not detect all cases of possible oscillation in a circuit design with multiple active devices. The stability analysis approach proposed by AMCAD is based on a pole-zero identification technique previously developed.11 The method can be applied to DC, small-signal, and large-signal stability analyses using simulations obtained in commercial CAE tools.
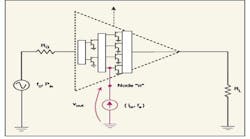
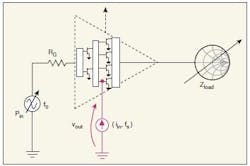
The AMCAD approach calculates a single-input, single-output (SISO) transfer function for a circuit of interest linearized about a given steady state. A simulated frequency response of the linearized circuit, H(jω) is fitted to a rational polynomial transfer function, H∧(s), by means of frequency-domain identification algorithms. If no poles on the right-half plane (RHP) are found in Ĥ(s) for the circuit being analyzed, it is considered stable. Figure 1shows how a circuit is analyzed. A sinusoidal small-signal current, iin, is connected in parallel at a particular circuit node as the excitation source. The voltage, vout, at this node is taken as the output of the system or circuit. The frequency, fs, is then swept and the frequency response is calculated as the impedance seen by the current probe at this particular circuit node:
H(jω) = Z(jω) = (vout)(jω)/iin(jω)
(1)
where H(jω) corresponds to a linearization of the circuit about a DC bias point obtained by sweeping fs in a linear AC simulation. System identification techniques are then applied to H(jω) to obtain Ĥ(s). The linearized circuit is stable if no poles of Ĥ(s) lie on the RHP.
1. This diagram represents a circuit for stability analysis, with a small-signal sinusoidal current source connected at a particular node.
For large-signal stability analysis, the ratio vout(jω)/iin(jω) represents the first term, H0(jω), of the harmonic series that comprises the linear time-variant transfer function resulting from linearizing the system under large-signal conditions. Term H0(jω) can be found by sweeping fs as part of a harmonic-balance (HB), mixer-like simulation in which the large-signal input drive serves as the mixer’s local oscillator (LO) and the small-signal current source at fs is the RF signal to the mixer. The same identification techniques applied for the small-signal case are used to find Ĥ0(s). The poles of Ĥ0(s) are directly related with the Floquet exponents of the linearized system, and thus provide the stability information for the large-signal steady state under study. The resulting pole-zero plots associated with Ĥ0(s) provide useful information about the critical frequencies at which a spurious oscillation can take place.
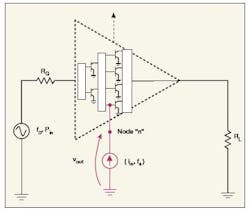
When working with the STAN tool, the first step is to connect a small current source to a node of the circuit under analysis. For simple circuits with a clear feedback structure, such as a single-stage amplifier or oscillator, any node should do. But for a multistage amplifier, one node per stage should be used. A linear or nonlinear simulation is then performed with a commercial CAE simulator of choice to obtain the frequency response of the circuit, H(jω). AMCAD offers simulation templates for both ADS from Agilent Technologies (Fig. 2) and Microwave Office from AWR. Different templates are used depending upon the type of analysis, such as an AC simulation for linear stability analysis or an HB simulation for nonlinear stability analysis. Both types of simulations use a similar methodology and both display H(jω) on a graph. This frequency response is then exported in a text file to be identified in the STAN tool.
2. Stability analysis templates, such as this nonlinear template for ADS 2011, are used to implement the AMCAD stability analysis capability with commercial CAE simulators.
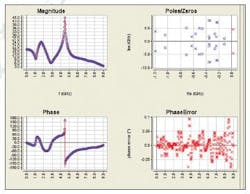
The second step of the stability analysis approach is to identify this frequency response H(jω) to find the transfer function, Ĥ(s), and the associated poles and zeros of that response. The STAN tool makes this possible by starting from a text file exported from a CAE simulator of choice to make the identification and analyze the results. The quality of this data fit is normally done by visual inspection, since the order of the transfer function is a priori unknown; normally an iterative process is used to find the order of the model, which can be quite cumbersome. A specially designed automated algorithm in the STAN tool12 helps speed and simplify this process, enabling the use of pole-zero identification for multivariable large-signal stability analyses that are otherwise impractical with manual quality assessment. The STAN tool features a straightforward graphical user interface (GUI) to further simplify the process (Fig. 3).
3. This is an example of the graphical user interface used with the STAN tool.
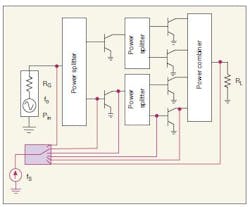
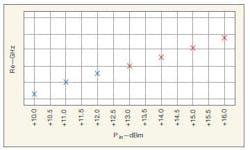
The STAN tool can perform analysis at several nodes (Fig. 4) as well as swept multiparameter analysis (Fig. 5), with simulation templates available for different conditions. The results make it possible to determine the kind of oscillation mode and the location in the circuit.13 As an example of these results, the poles-zeros graph of Fig. 6 shows the evolution of the poles versus input power for a simple amplifier with two transistors in parallel. It shows the input drive level at which oscillation starts in this circuit design.
4. This diagram shows how a multinode stability analysis would be performed on an RF/microwave amplifier.
5. Parametric analysis of an amplifier under study is performed by simulating different load conditions.
6. This plot of poles versus input power shows oscillation starting with +13 dBm input power.
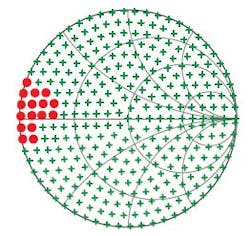
A more complex example is a three-stage LDMOS distributed power amplifier for a software-defined-radio (SDR) application.12 A prototype is stable with a 50-Ω load under nominal operating conditions, but the design had to be evaluated under a wide range of conditions (including with high reflective loads). Large-signal analyses were carried at while varying input power, frequency, and the load impedance. Figure 7 shows areas on the Smith chart leading to instability—results which have been experimentally validated.
7. The green and red represent stable and unstable regions in the ΓL plane for input power of +17.1 dBm at input frequency of 500 MHz.
The STAN tool can also be used for Monte Carlo stability analysis, as was demonstrated with an L-band FET amplifier at 1.2 GHz.14 The prototype had exhibited low-frequency instability associated with the bias circuitry. This instability can be corrected with the inclusion of a gate-bias resistor. The STAN tool was used to determine the value of the resistor for adequate stability margin. Figure 8 shows pole-zero identification results for two different values of stabilization resistance for the L-band amplifier; some instability existed for 44 Ω, while the 70-Ω resistance yielded stable operation for all conditions. By applying Monte-Carlo analysis techniques, the STAN tool is suitable for systematic stabilization of multi-transistors circuits.15
8. These pole-zero maps of the FET amplifier were obtained for the two values of
stabilization resistance shown.
AMCAD Engineering, Batiment Galileo, 20 rue Atlantis, 87068 Limoges, France; +33 (0) 555-040-531, FAX: +33 (0) 555-040-531, www.amcad-engineering.com.
References
1. J.M. Rollet, "Stability and Power-Gain Invariants of Linear Two Ports," IRE Transactions on Circuit Theory, Vol. 9, No. 1, March 1962, pp. 29-32.
2. W. Strubble and A. Platzker, "A Rigorous Yet Simple Method For Determining Stability of Linear N-Port Networks," 15th Gallium Arsenide Integrated Circuits (GaAs IC) Symposium Technical Digest, October 1993, pp. 251-254.
3. M. Ohtomo, "Stability Analysis and Numerical Simulation of Multidevice Amplifiers," IEEE Transactions on Microwave Theory and Techniques, Vol. 41, No. 6/7, June/July 1993, pp. 983-991.
4. T. Narhi and M. Valtonen, "Stability Envelope: New Tool for Generalised Stability Analysis," IEEE MTT-S International Microwave Symposium Digest, Vol. 2, June 1997, pp. 623-626.
5. V. Rizzoli and A. Lipparini, "General Stability Analysis of Periodic Steady-State Regimes in Nonlinear Microwave Circuits," IEEE Transactions on Microwave Theory and Techniques, Vol. 33, No. 1, January 1985, pp. 30-37.
6. S. Mons, et al., "A Unified Approach for the Linear and Nonlinear Stability Analysis of Microwave Circuits Using Commercially Available Tools," IEEE Transactions on Microwave Theory and Techniques, Vol. 47, No. 12, December 1999, pp. 2403-2409.
7. A. Suarez, et al., "Nonlinear Stability Analysis of Microwave Circuits Using Commercial Software," IEEE Electronics Letters, Vol. 34, No. 13, June 1998, pp. 1333-1335.
8. P. Bolcato, et al., "Efficient Algorithm for Steady State Stability Analysis of Large Analog/RF Circuits," IEEE MTT-S International Microwave Symposium Digest, Vol. 1, May 2001, pp. 451-454.
9. G. Leuzzi and F. Di Paolo, "Bifurcation Synthesis by Means of Harmonic Balance and Conversion Matrix," Proceedings of Gallium Arsenide Applications Symposium, October 2003, pp. 521-524.
10. M. Mochizuki, et al., "Nonlinear Analysis of f0/2 Loop Oscillation of High Power Amplifiers," IEEE MTT-S International Microwave Symposium Digest, Vol. 2, May 1995, pp. 709-712.
11. J. Jugo, J. Portilla, A. Anakabe, A. Suarez, and J.M. Collantes, "Closed-loop stability analysis of microwave amplifiers," IEEE Electronics Letters, Vol. 37, February 2001, pp. 226-228.
12. A. Anakabe, et al., "Automatic Pole-Zero Identification for Multivariable Large-Signal Stability Analysis of RF and Microwave Circuits," Proceedings of the 40th European Microwave Conference, September 2010, pp. 477-480.
13. A. Anakabe, J.M. Collantes, J. Portilla, J. Jugo, S. Mons, A. Mallet, and L. Lapierre, "Analysis of Odd-Mode Parametric Oscillations in HBT Multi-Stage Power Amplifiers," European Microwave Week, 11th GaAs Symposium, October 2003, pp. 533-536.
14. J.M. Collantes, N. Otegi, A. Anakabe, N. Ayllon, A. Mallet, G. Soubercaze-Pun, "Monte-Carlo Stability Analysis of Microwave Amplifiers," 12th Annual IEEE Wireless and Microwave Technology Conference (WAMICON), April 2011.
15. N. Ayllon, J.M. Collantes, A. Anakabe, I. Lizarraga, G. Soubercaze-Pun, and S. Forestier "Systematic Approach to the Stabilization of Multitransistor Circuits," IEEE Transactions on Microwave Theory and Techniques, Vol. 59, No. 8, August 2011, pp. 2073-2082.
Collaborating In Quest Of Stability
Maury Microwave Corp. (Ontario, CA) and AMCAD Engineering (Limoges, France) began collaborating in 2010 to blend their knowledge and experience in measurement and modeling device characterization. Maury Microwave and AMCAD—along with their partner, Agilent Technologies—provide numerous measurement solutions. These include active, passive, and hybrid nonlinear harmonic load-pull measurement capabilities, ranging from a few MHz through 110 GHz using Maury’s automated impedance tuners and IVCAD software.
The vector-receiver load-pull capability offered by Maury/AMCAD (sometimes referred to as real-time load-pull capability) is achieved by using low-loss couplers between the tuner and a device under test (DUT), then measuring the calibrated
a- and b-waves from the DUT in real time for each impedance and drive power presented to the DUT. A variety of parameters, including intermodulation parameters and vector parameters such as AM-to-PM distortion, can be calculated from these waves.
Harmonic load-pull measurements can be accomplished by using mechanical tuners (multiple single-frequency tuners joined together with a multiplexer or cascaded serially, or multi-frequency single-box harmonic tuners), active tuning chains (consisting of a magnitude and phase controllable signal generator and amplifier), or a combination of both.