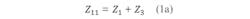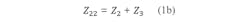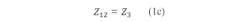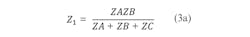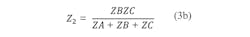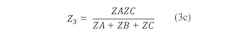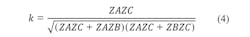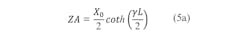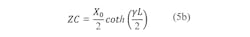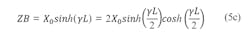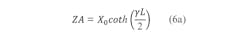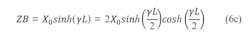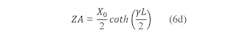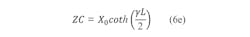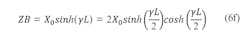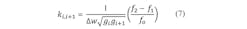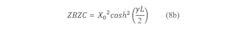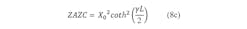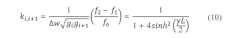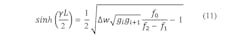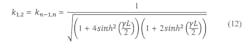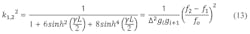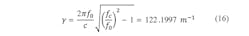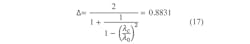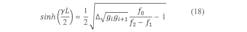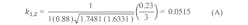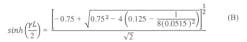Filters are important components in many high-frequency systems, from commercial communications to electronic warfare (EW). A wide range of filters are useful at RF/microwave frequencies, including coaxial, cavity, stripline, microstrip, and waveguide configurations. While they tend to be large, waveguide filters offer high-quality-factor (high-Q) performance with low loss. Evanescent-mode waveguide filters can provide similar high-Q performance as propagating-mode waveguide filters, but in somewhat smaller structures. What follows is a method to design these filters without the need for time-consuming iterative methods.1-4
1. This simple block diagram shows a classical T network.
This file type includes high resolution graphics and schematics.
Figure 1 shows a T-coupled structure used in evanescent-mode waveguide filters, for which the equations can be written as:
For the coupling coefficient (k) between the two loops of the T-coupled structure, Eq. 2 can be applied:
2. This block diagram represents a classical Π network.
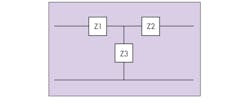
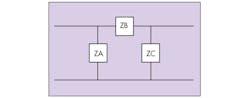
Figure 2 shows a Π-coupled structure. Using a delta-star transformation yields the relationships of Eq. 3:
Substituting the definitions of Eq. 3 into Eq. 2 yields Eq. 4:
This file type includes high resolution graphics and schematics.
Evanescent-Mode Waveguide Length
This file type includes high resolution graphics and schematics.
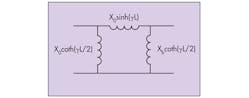
3. This block diagram shows the evanescent-waveguide equivalent circuit.
Figure 3 shows the schematic of an evanescent-mode waveguide length as a Π network. The relationships in Eq. 5 are valid for any of the internal resonators:
where:
X0 = the reactive impedance of the evanescent waveguide filter;
γ = the complex propagation constant in the evanescent waveguide; and
L = the length of the evanescent waveguide resonator.
For the end resonators, the relationships in Eq. 6(a)-6(c) can be used:
Similarly, for the output resonator, Eqs. 6(d-f) can be used:
From Seymour Cohn’s classic work on filters:5
where:
w = 2πf = 1 = the cutoff frequency of the lowpass prototype;
g = the normalized elements of the lowpass prototype; and
ki, i + 1 = the coupling coefficient between sections i and i + 1.
This file type includes high resolution graphics and schematics.
Internal Resonators
This file type includes high resolution graphics and schematics.
For the internal resonators:
From Eqs. 4 and 8, it is possible to obtain Eq. 9:
From Eqs. 9 and 7, the coupling coefficient, ki, i + 1, can be found in Eq. 10:
Finally, by rearranging Eq. 10, length L can be calculated from Eq. 11:
For the first and the last resonators, Eqs. 12-15 provide important insights:
This file type includes high resolution graphics and schematics.
Filter Design Examples
This file type includes high resolution graphics and schematics.
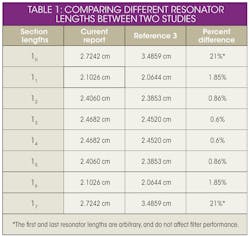
A pair of filter design examples may help to demonstrate the effectiveness of the current, non-iterative design method. An evanescent mode filter can be designed using closed-form Eqs. 11 and 15. To check the results of the current design approach, they are compared in Table 1 with the example presented in ref. 3, which employed a lengthier iterative design approach. Given that the center frequency, fc, is 6.5571 GHz, and the cutoff frequency, f0, is 3 GHz, the ripple for this example lowpass filter is 0.01 dB and the minimum stopband attenuation is 50 dB at 328 GHz. The design employs WR-90 ridged waveguide, with a length, L, of 0.9 in. (2.29 cm) and width, W, of 0.4 in. (1.02 cm), which leads to:
The prototype parameters for this first example lowpass filter include g0 = 1; g1 = 0.7969; g2 = 1.3924; g3 = 1.7481; g4 = 1.6331; g5 = 1.7481; g6 = 1.3924; g7 = 0.7969; and g8 = 1, with differential, Γ, given by Eq. 17:
Solving for the inner resonators yields Eq. 18:
and results in the following values for the inner resonators:
l1 = l6 = 2.1026 cm; l2 = l5 = 2.4060 cm; and l3 = l4 = 2.4682 cm.
To solve for outer resonators, the largest g values are used. Since the outer resonator lengths are arbitrary, the largest g values are chosen to minimize the reflection from the end walls of the filter:
resulting in the following values: l0 = l7 = 2.7242 cm.
This file type includes high resolution graphics and schematics.
Value Comparison
This file type includes high resolution graphics and schematics.
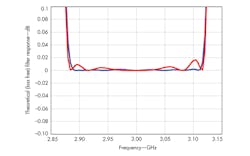
Table 2 compares the resonator values of this first filter example to the example produced in ref. 3. The results of the comparison are also depicted in Fig. 4. As can be seen from the comparison of the two example filters, while the closed-form equations presented in the current report are not quite as accurate as the relations used in ref. 3, they are easier to implement and deliver reasonable results.
4. These graphs represent the iterative method developed by Howard and Lin3 (blue line) and the results of using the closed-form equations from the current report (red line).
For a second comparison of example filters, the example of ref. 2 will be used. It is a five-section Chebyshev filter with 0.01-dB ripple and 1% bandwidth at 4 GHz. The lowpass prototype parameters for this filter design are g0 = 1; g1 = 0.7563; g2 = 1.3049; g3 = 1.5773; g4 = 1.3049; g5 = 0.7563; and g6 = 1. Using Eq. 17, Δ is found to be 0.7716. Using Eq. 18 to find the inner resonators result in the following: l1 = l4 = 3.9964 cm and l2 = l3 = 4.3303 cm.
Equations 13 and 15 are used to find the outer resonator lengths. Since these are arbitrary, the largest g values are chosen to calculate the lengths for the outer resonators. The outer lengths then are l0 = l5 = 4.6432 cm.
As Fig. 5 shows, the results of the interactive method of ref. 2 and the closed-form method of the present report are much closer, as the bandwidth for these example filters is much more narrow (1%). The bandwidth plotted in Fig. 4 is much wider (about 7.5%) and the results between those two methods (the present approach and ref. 3) are more diverse.
5. These graphs offer the iterative method of Craven and Mok2 (blue line) and the results of using the closed-form equations from the current report (red line).
This file type includes high resolution graphics and schematics.
Coaxial Launcher Types
This file type includes high resolution graphics and schematics.
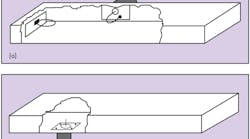
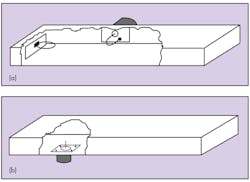
Part of designing an evanescent-mode waveguide filter is to employ effective launchers. Figure 6 illustrates two types of coaxial launchers. Launchers can be coaxial types, propagating waveguide types, and microstrip-to-evanescent waveguide transformers.
6. These diagrams show (a) a magnetic-loop RF launcher and (b) an electric-field-probe RF launcher.
Related Articles • Filtering EMI And RFI Noise • Single CDTA Leads To Multiple Filters • Single Filter Has Many ResponsesThe resistance of an evanescent-mode waveguide filter can be calculated by applying Eq. 35 from ref. 3; it can also be found by experimental methods. To tune the launcher, the probe or the magnetic loop can be moved closer to or further from the first resonator on the filter. An evanescent-mode waveguide filter is a unique type of filter that provides high Q in a relatively small size compared to other types of filters. By using the design methods shown here, reasonable results can be achieved without the long times required for iterative methods.
Dr. John Howard, President
Steve Jalil, Wireless Engineer
Electromagnetic Technologies Industries, Inc., 50 Intervale Rd., Boonton, NJ 07005; (973) 379-1719, FAX: (973) 379-1651.
Acknowledgment
The authors would like to express their thanks to Mr. Sertac Sayin for his helpful comments on the subject.
References
1. John Howard and M. Lavey, “Simplified Method Eases The Design Of Bandpass Filters,” Microwaves & RF, Vol. 39, No, 13, December 2000, pp. 97, 98, 230, 232.
2. G. Craven and C. Mok, “The Design of Evanescent Waveguide Bandpass Filter for a Prescribed Insertion Loss Characteristic,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-19, March 1971.
3. John Howard and W. Lin, “Evanescent Mode Filter: Design and Implementation,” Microwave Journal, Vol. 32, October 1983, pp. 121-136.
4. Richard V. Snyder, “New Applications of Evanescent Mode Waveguide Filter Design,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-25, December 1977.
5. Seymour B. Cohn, “Direct Coupled Resonator Filters,” Proceedings of the IRE, Vol. MTT-5, February 1957, pp. 187-196.
This file type includes high resolution graphics and schematics.