Download this article in PDF format.
Successful operation of in-flight internet and entertainment services requires accurate polarization alignment of the satellite and receive antennas for linearly polarized signals. Typically, the polarization alignment of the satellite and transceiver is accomplished by an electromechanical device that either rotates the antenna feed or other spatially operated devices that rotate the received signal vector. As will be seen, it is possible to provide the same rotational adjustment by means of a solid-state approach, rotating a received signal vector such that the result provides the original signals transmitted with cross-contamination from the other polarization removed.
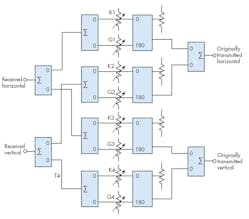
1. This block diagram shows the hybrid construction of an RF vector rotator.
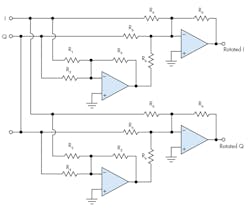
Figure 1 shows a block diagram of the vector rotator circuit, based on a low-frequency operational-amplifier (op-amp) circuit described in an earlier article.1 Whereas the low-frequency op-amp version had the advantage of being frequency-invariant over the usable range of op amps, it was limited in frequency by those same devices. That basic low-frequency version is shown in Figure 2.
2. This is a low-frequency version of the vector rotation circuit.
The proposed hybrid circuit performs the same vector rotation, but is better suited for microwave and millimeter-wave frequencies. The op amps in the original circuit perform the function of summing and subtraction of the scaled in-phase (I) and quadrature (Q) input signals. In the hybrid circuit, the inverting and adding functions are provided by 180-deg. hybrids, and the purely summation function is provided by 0-deg. power combiners. The op-amp circuit used resistors to set the scale factor of the input I and Q vectors, whereas in the hybrid circuit, attenuators set the scale factors.
The theoretical operation of the circuit is based on the vector representation of the received signals represented in eq. 1:
SR = [HTcos(ϕ) – VT sin(ϕ)]xˆH + [HTsin(ϕ) +VTcos(ϕ)]ŷV (1)
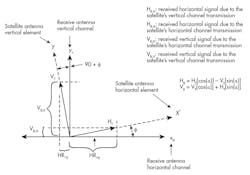
where SR is the received signal; HT is the transmitted horizontal signal; VT is the transmitted vertical signal; xˆH is the received horizontal signal reference axis; ŷV is the received vertical signal reference axis (where xH is the horizontal channel and yV is the vertical channel); and ϕ is the angle of misalignment between the transmit and receive antennas.
3. Satellite antenna misalignment results in cross-channel coupling.
Figure 3 illustrates the relationship between the satellite's antenna reference system and the earth, or in-flight transceiver’s antenna reference system. If you assume that all hybrids have the same insertion loss (−3 dB) for each input to output, and normalize the output amplitude by the overall loss factor, then the output can be written as:
V0 = HT[m1cos(ϕ) + m2sin(ϕ)]
+VT[m2cos(ϕ) – m1sin(ϕ)]
where m1 = k1 – G1 and m2 = k2 – G2.
If m1 = cos(ϕ) and m2 = sin(ϕ), then:
V0 = HT[cos2(ϕ) + sin2(ϕ)] + VT[cos(ϕ)sin(ϕ) – cos(ϕ)sin(ϕ)] → V0 = HT
In a similar derivation for the output of the vertical channel:
V0 = HT[m3cos(ϕ) + m4sin(ϕ)] + VT[m4cos(ϕ) – m3sin(ϕ)]
where m3 = k3 – G3 and m4 = k4 – G4.
If m4 = cos(ϕ) and m3 = –sin(ϕ), then V0 = HT[–sin(ϕ)cos(ϕ) + sin(ϕ)cos(ϕ)] + VT[cos2(ϕ) + sin2(ϕ)] → V0 = VT
Using the preceding determination for m1, m2, m3, and m4 dictates the following relationships:
k1 – G1 = cos(ϕ);
k2 – G2 = sin(ϕ);
k3 – G3 = -sin(ϕ);
k4 – G4 = -cos(ϕ);
These relationships can be realized with the following equations:
k1 = cos2(ϕ); G1 = k1 – cos(ϕ);
k2 = 0.5 + 0.5sin(ϕ); G2 = k2 – sin(ϕ);
G3 = 0.5 + 0.5sin(ϕ); k3 = G3 – sin(ϕ);
k4 = cos2(ϕ); G1 = k1 – cos(ϕ);
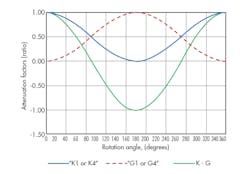
Plots of the k and G values are shown in Figures 4, 5, and 6.
4. Attenuation factors K1 and K4 and G1 and G4 are plotted here.
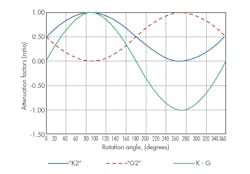
5. Attenuation factors K2 and G2 are plotted as a function of rotation angle.
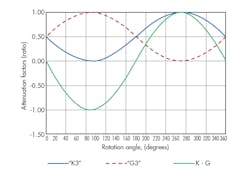
6. Attenuation factors K3 and G3 are plotted as a function of rotation angle.
Detailed derivation along with a spreadsheet model (Fig. 7) that allows for variation of all hybrid losses, phase differences, and interconnecting parameters is available upon request. The spreadsheet model does not lend itself to complicated variations of the components and interconnecting lines, but does allow investigations of real circuit tolerances to the extent of manual effort tolerated by the investigator. An Octave-based program is being developed to make it easy to manipulate the myriad of variables in an actual circuit fabrication.
7. This spreadsheet model of the solid-state vector rotator includes the effects of variations due to hybrid losses, phase differences, and interconnecting parameters.
Reference:
1. R.C. Monzello, "Circuit Provides Frequency-Independent Quadrature Rotation," Microwaves & RF, September 1995.