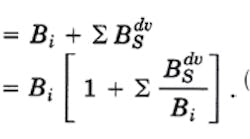Scatterers such as rainfall can impose hard-to-predict effects on the propagation of electromagnetic (EM) waves, often making analysis of the near-field and far-field antenna patterns and performance difficult. In order to provide a more meaningful approach to understanding the effects of scatterers on EM propagation, last month Part 1 of this study explored the influence of distributed scatterers on nearfield antenna EM propagation. Part 2 will now be extended to include a precipitation region containing many raindrops, with precipitation contained between the planes z = z1 and z = z2 and with the elemental volume dv located at plane z.
From last month, the following relationships need tobe re-established:
When no precipitation is present, E3H3 is identical to E1H1. But when precipitation is present, E3 and E1 are related by the effective complex refractive index, m^ ,of the precipitation region:
E3 = E1 exp1> (26)
where z1 z z2. Equation 26 gives the transmitter field (i.e., the field due to antenna 1 in the presence of precipitation) in the elemental volume dv (Fig. 3). Equation 25 can be used to find the wave detected by the receiving antenna due to scattering by raindrops:
where E1 and E2 are the complex scalar amplitudes of field vectors E1 and E2, respectively.
Assuming single scattering and a sufficient number of drops present in the elemental volume, the wave detected at the receiving antenna due to scattering from all raindrops in the precipitation region can be found by integrating Eq. 27:
where vol indicates integration over the precipitation volume, i.e., the region between z = z1 and z = z2. Because the beamwidth of the transmit and receive antennas is very small, the volume integral in Eq. 28 may be written
and Eq. 28 becomes
It is useful at this point to recognize the significance of two equations, Eqs. 9 and 30. It has already been shown that the received wave in the absence of precipitation is given by the relationship for B1 in Eq. 9. And Eq. 30 gives the received EM wave due to scattering from all the raindrops in the precipitation region. The total wave received in the presence of precipitation is
From Eqs. 9 and 30,
Using this in Eq. 31,
Defining a and as the total attenuation (in Nepers) and phase shift (in rads), respectively, due to the precipitation, then
Comparing Eqs. 33 and 34 yields
Parameters m and S(0) can be shown to be related by the simple formula
m = 1 j(2 /k3)NS(0)
Using this relationship in Eq. 35 results in
In naturally occurring rainfall, the raindrops will have a drop size distribution, m , given by
where a is the mean drop radius. If the rate of precipitation is uniform throughout, m will be independent of z and Eq. 36 becomes
The integralcan be written as
where A is the beamwidth cross section of the common volume of propagation of the two antennas.
Continue to next page.
Page Title
Then
SEE EQUATION H
and
for any plane z normal to the direction of propagation. Using Eq. 39 in Eq. 38,
SEE EQUATION I
and
SEE EQUATION 40
SEE EQUATION 41
SEE EQUATION 42
This analysis has included the effects of scatterers in the near-field as well as the far-field regions of the transmit and receive antennas in a communications link. It shows that scatterers such as rain will introduce the same attenuation and phase shift whether in the near-field or far-field regions, and the same depolarization effects.
Editor's Note: This article is based on an article by the author entitled "A General Scattering Theory," first appearing in RCA Review, September 1983.
REFERENCES
1. B. J. Easterbrook and D. Turner, "Prediction of Attenuation by Rainfall in the 10.7-11.7 GHz Communications Band, Proceedings of the IEEE, Vol. 114, 1967, p. 557.
2. L. C. Tillotson, "A Model of a Domestic Satellite Communication System," Bell System Technical Journal, Vol. 47, 1968, p. 2111.
3. D. C. Hogg and T. S. Chu, "The Role of Rain in Satellite Communications," Proceedings of the IEEE, Vol. 63, No. 9, 1975, p. 1308.
4. D. C. Hogg and T. S. Chu, "Propagation of Radio Waves at Frequencies Above 10 GHz," IEE Conference Publication 98, 1973.
5. W. E. Lothalier, "System Considerations for European Communication Satellites," IEEE International Conference o Communication, Philadelphia, PA, 1972, pp. 2-1 to 2-7.
6. J. W. Ryde, "Attenuation of Centimetre Waves by Rain, Hail, and Clouds," Report 8516, General Electric Company Research Labs, Wembley, England, 1944.
7. H. C. Van de Hulst, Light-Scattering by Small Particles, Wiley, New York, 1957, p. 28.
8. R. G. Medhurst, "Rainfall Attenuation of Centimeter Waves: Comparison of Theory and Measurement," IEEE Transactions on Antennas and Propagation, Vol. AP-13, 1965, p. 55.
9. J. W. Mink, "Rain-Attenuation Measurements of Millimeter Waves Over Short Paths," Electron Letters, Vol. 9, No. 10, 1973, p. 198.
10. R. K. Crane, "The Rain Range ExperimentPropagation Through a Simulated Rain Environment," IEEE Transactions on Antennas and Propagation, Vol. AP-22, 1974, p. 321.
11. D. P. Haworth, N. J. McEwan, and P. A. Watson, "Effect of Rain in the Near Field of an Antenna," Electron Letters, Vol. 14, No. 4, 1978, p. 94.
12. J. Van Bladel, Electromagnetic Fields, McGraw-Hill, New York, 1964, p. 254.