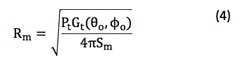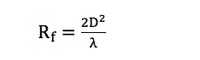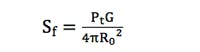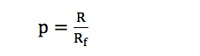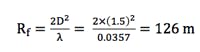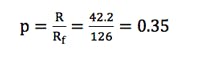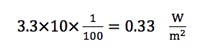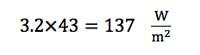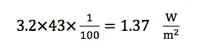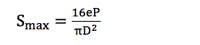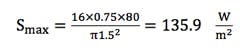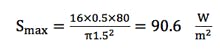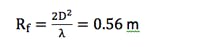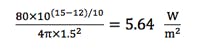Download this article as a .PDF
The electromagnetic (EM) energy radiated from an antenna may exceed the limits of safe human exposure, especially when the safe power levels and field intensities at different frequency bands are specified. Determining whether the safety criteria are satisfied when in a close vicinity of a large parabolic reflector antenna requires the knowledge of the near-field parameters.
In this article, existing methods are used to estimate these parameters, which are then compared with industry standards, such as the Federal Communications Commission’s (FCC) OET Bulletin 65 or Health Canada’s Safety Code 6, to determine the safe distance.2, 3 The results provided are for reference only and the user must measure the field parameters to ensure safety.
Introduction
As a provider of different types of antennas for satellite communications (satcom), Norsat International and many other companies conduct numerous tests to evaluate product performance. In a recent Norsat project, an X-band terminal underwent a Wideband Global Satcom (WGS) certification process. The antenna had to transmit up to 80 W for multiple 24-hour sessions in order to demonstrate its compliance with the MIL-STD-188 164B standard.1 To ensure the protection of the staff and public, Norsat used industry safety standards to determine safe human-exposure levels.
The exposure limits, in both FCC Bulletin 65 and Safety Code 6, are provided in terms of the electric field intensity, magnetic field intensity, and power density. To compute these parameters using simple and conventional methods, the observer must be in the far field of the antenna, which is the region beyond the Fraunhofer distance.
As Norsat staff members would approach the antenna regularly, it was essential to establish the safety rules for the near-field region as well. Hence, the field parameters at positions closer than the Fraunhofer distance had to be determined. In this article, we will focus solely on the power density.
Farrar and Chang provide a series of figures and a guideline for estimating the field parameter in the near-field region.4 However, the shortcoming of this method is that it is only valid on the axis of the boresight of the antenna.
For a given radial distance in the near-field region, Kobayashi provides an estimate of the ratio by which the near-field power and field intensities are reduced versus the offset angle from the boresight axis.5
Using both references, the power and field intensities can be estimated at different distances and offset angles from the boresight in the near-field region. Areas with power considered hazardous by industry standards are cordoned off and access is blocked.
The section below reviews the theory for power-density calculation at far field and presents a summary of the method of estimating the power density in the near field. Later on, we will apply this method to a practical problem and determine the safe distances from the antenna.
Electromagnetic Power Density and Safety Guidelines
The power density, S, radiated from an antenna with a gain of Gt and at distance of R is given by:
provided the distance, R, is greater than the Fraunhofer distance, which defines the far-field region. The Fraunhofer distance is determined by:
where D is the largest dimension of the antenna and λ is the wavelength.
If located in the far-field region, the power density computed by Eq. 1 can be compared to the exposure limits defined by OET Bulletin 65 or Safety Code 6.
Safety in the Far Field
Safety Code 6 defines the exposure limits differently for controlled and uncontrolled environments. The uncontrolled environments have more conservative limits. For an X-band signal in uncontrolled environments, the maximum RMS value of the electric field intensity (Em), the maximum RMS value of the magnetic field intensity (Hm), and the maximum power density (Sm) are as follows:
Em = 61.4 (V/m)
Hm = 0.163 (A/m)
Sm = 10 (W/m2)
OET Bulletin 65 of FCC provides the same exposure limit of 10 W/m2 for power density for X-band signals.
In the far field, it is sufficient to satisfy the power-density criterion since the other two parameters are directly related to the power density and the wave impedance.
Knowing the gain of the antenna and the transmitted power, we can compute the distance at which the power density is Sm. This distance is denoted by Rm and determined by:
Rm computed by Eq. 3 is accepted only if it is larger than Rf. The distance Rm is usually computed for the boresight. However, if the observer is away from the boresight by elevation and azimuth angles of θo and φo, respectively, we then have:
which will result in a smaller distance as the gain, Gt(θo, φo), away from the boresight is significantly smaller than the gain at the boresight for any offset angles significantly larger than half-power beamwidth.
Safety in the Near Field
In the near-field region, some approximations are required to estimate the power density. The National Telecommunications and Information Administration (NTIA), located within the Department of Commerce, has a series of documents in which such approximations and procedures are provided.4, 5
First, we must determine the far-field power density at the boundary of the far-field and Fresnel regions (S0). Then the procedure to estimate the power density in closer distances is mainly divided into three sections:
- Determine the tapering factor of dish illumination, which shows how uniformly the dish is illuminated. A tapering factor of n = 0 means that the feed antenna illuminates the dish uniformly. As n increases, illumination rapidly decreases by moving away from the center of the reflector.
- Determine the correction factor for power density along the boresight in the Fresnel or near-field regions.4
- Determine the correction factor for the off-boresight angle.5
Correction factors depend on the tapering factor of the dish. We apply the correction factors to S0 and estimate the power density at the desired point.
The above items are described in more detailed steps as follows:
1. Determine the tapering factor, n.
- Determine λ/D, where D is the diameter of the dish and λ is the wavelength at the largest frequency.
- Determine the half-power beamwidth from gain patterns, θ.
- Determine the θ/(λ/D), and compare it to the factor in the second column of Table 1 on Page 3-2 of ref. 5. Based on this comparison, choose a tapering n from the first column.
2. Determine the Fraunhofer distance:
3. Determine field power density at Rf:
where G is the numerical value of the gain of the antenna.
4. Determine the normalized distance:
5. Use Figure 4-3(b) in ref. 4 to determine the on-axis power density for p and n = 1. If tapering is different, use the applicable plots in Figures 4-3.
6. Determine the off-axis angle according to the desired observation point.
7. Use Figure 3-10e in ref. 5, assuming n = 1, to determine the correction factor. Apply the correction factor.
Application to an 80-W, 1.5-m Antenna
An 80-W, X-band antenna with a 1.5-m reflector was used in this project. At the largest frequency, 8.4 GHz, the wavelength is 0.0357 m and the diameter of the parabolic reflector antenna is 1.5 m. Using Eq. 2, we determine the Fraunhofer distance:
At this distance, the power density of our terminal is computed by Eq. 1. The computed result is 3.2 W/m2, less than 10 W/m2.
Hence, for all off-boresight angles, if the radial distance from the antenna is 126 m or more, the exposure to EM power will be within the safety limits.
Safety at a Specific Position
Given the geometry of our test location, we were interested in knowing the power density at distance of R = 42.2 m. Since R < Rf and we are in the Fresnel region, it is required to go through the steps defined in the previous section.
At 8.15 GHz, our test frequency, the half-power beamwidth, is about 1.74 degrees, which equals θ = 0.0304 radians and λ = 0.0368 m. Therefore, λ/D = 0.024.
Hence, θ/(λ/D) = 1.24, which is close to the factor 1.27 in column 2 of Table 1 on Page 3-2 in ref. 3. As a a result, n = 1. The tapering factor is assumed to be the same at all frequencies of the transmit band.
The smallest distance that can be considered far field at 8.15 GHz for a 1.5-m dish is about 122 meters. At this distance, the power density of our terminal is:
So the normalized distance is computed by:
The correction factor obtained from Figure 4-3 (b) in ref. 2 at p = 0.35 is about 10. Hence, the power density at this distance, on the boresight axis, is about 3.3 × 10 = 33(W/m2), which is above the safety requirement.
To ensure the safety at this location, we introduce a cone with an apex angle of 20 degrees around the boresight axis. Nobody is allowed to enter the conic section. So at the edge of the cone, the offset angle is 10 degrees. To show that the exposure is within the safety limit at this angle, we use Figure 3-10e in ref. 3. In this figure, the correction factor for angles above 10 degrees is well below −20 dB, which is 1/100 for power density.
Hence, the power density at a radial distance of 42.2 meters and 10 degrees away from the boresight is less than:
which is far less than 10(W/m2) as recommend by ref. 1.
In this case, a 20-degree cone, 10 degrees from boresight, provided a good safety level. This can be verified at a worst-case scenario.
Worst-Case Scenario
Figure 4-3(b) of ref. 4 shows that the highest correction factor of 43 occurs at the normalized distance of about 0.1. Therefore, the maximum on-boresight power density is:
At the edge of the 20-degree cone, the 10-degree offset angle correction factor, as shown by Figure 3-10e, is well below 1/100. Hence, the power density is less than:
which is less than 10(W/m2), as recommend by refs. 2 and 3.
The offset angles usually assume that the radiating antenna is a point-source. To ensure safety, it is recommended that the unsafe region is extended such that it encompasses the 20-degree cone plus a margin of D/2 = 75 cm.
The FCC Approach to the Worst-Case Scenario
In the FCC OET Bulletin 65, the maximum on-boresight near-field power density is approximated by:
where e is the aperture efficiency and is usually between 0.5 and 0.75. Considering an aperture efficiency of 0.75, the maximum power density is:
which is very close to the value computed at the previous section.
However, due to the radome effects, the total efficiency of our antenna is close to 0.5. As a consequence:
Considering the 1/100 factor obtained in the previous section, the power density at an offset angle of 10 degrees will be 1.359 or 0.906(W/m2), which is less than the exposure limit.
Standing Behind the Reflector
The technical staff may have to approach a transmitting antenna in order to conduct regular maintenance. Here we determine the power density at locations behind the reflector, where there is line-of-sight to the feed antenna. It is not possible to use the method described in the previous section because the correction factor for an off-boresight angle of larger than about 30 degrees is expected to be very small; therefore, it is not provided in ref. 5. The power density computed with this method would be negligible.
Here, to estimate the power density behind the antenna, the spillover effect will be considered. The diffraction that occurs at the edge of the reflector is not accounted for.
Assuming that the largest dimension of the feed of the antenna is 10 cm, the Fraunhofer distance at 8.4 GHz is:
Therefore, a person standing almost behind the reflector at a place from where the feed is visible will be at the far field of the feed antenna. As a result, the transmitted power and the gain of the antenna will be needed to compute the power density leaked to the region behind the reflector where the feed is visible. We cannot use the tapering factor discussed in previous section, as it is does not have the desired accuracy for this purpose.
Given that the gain of the feed of the antenna is about 15 dB and the tapering is 12 dB at the edge of the main reflector, then for a person standing about 1.5 m from the feed, behind the antenna and near the edge of reflector, the power density is:
This value is only about 3 dB below the recommended value by Safety Code 6. Hence, a person standing close behind the reflector may choose not to stay for a long time when the antenna is transmitting with full power.
Conclusion
This article provides a step-by-step method for determining the power density of a radiating parabolic reflector antenna in the far- and near-field regions.
We reviewed the safety guidelines in FCC OET Bulletin 65 and Health Canada’s Safety Code 6 for human-exposure limits to EM radiation, as well as the power-density calculation in the far field. In the near-field region, the field was estimated in two major steps. After determining the power density at the Fraunhofer distance, a correction factor was applied to approximate the power density on boresight at the closer distance. A second correction factor was applied to estimate the power density at an offset angle. The correction factors were obtained from refs. 4 and 5.
Comparing the results to the guidelines of Safety Code 6 will enable companies conducting outdoor tests to determine the safe region and block access to the unsafe region to ensure the safety of their staff and other public members.
The methods reviewed are limited to reflector antennas. Dipole, Yagi, or other types of antennas must be treated differently and are out of the scope of this article.
The computed distances, angles, and safety margins are only valid for the described antenna. It is the responsibility of the reader to apply the method discussed in this article to his or her problem of interest.
Disclaimer: The results provided in this article are for reference only; the user must measure the field parameters to ensure proper safety.
References:
1. U.S. Department of Defense, MIL-STD-188 165A, 2012.
2. Federal Communications Commission: Office of Engineering & Technology, Evaluating Compliance with FCC Guidelines for Human Exposure to Radiofrequency Electromagnetic Fields, 1997.
3. Health Canada, Limits of Human Exposure to Radiofrequency Electromagnetic Energy in the Frequency Range from 3 kHz to 300 GHz (Safety Code 6), 2015.
4. A. Farrar and E. Chang, Procedures for Calculating Field Intensities of Antennas, 1987.
5. H. K. Kobayashi, Procedure for Calculating the Power Density of a Parabolic Circular Reflector Antenna, 1990.