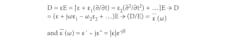Study the Loss of Microstrip on Silicon

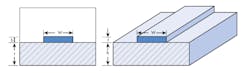
1. The diagram depicts a microstrip transmission line with conductor width w and height h, enclosed in a box not considered as part of the loss analysis.

Figure 1 shows a microstrip transmission line with conductor width w and height h, enclosed in a box not considered as part of the loss analysis. Dielectric constant is the key material parameter involved in quantifying the intrinsic capacitance between conductors. In time-varying electric fields, dielectric loss represented by the substrate material’s loss tangent is taken into consideration. Due to the field distribution in microstrip, the effective dielectric constant, ɛ_eff, has a lower value than the relative permittivity or relative dielectric constant, ε_r, of the substrate material. The effective dielectric constant, ε_eff, can be found by means of

ε_eff = C/C_a = (c/v_p)²

where C is the capacitance of the microstrip on a dielectric material and C_a is the capacitance of the microstrip structure considering vacuum in place of the dielectric.

A general expression for ɛ_eff is

ɛ_eff =  [(ɛ_r + 1)/2] + [(ɛ_r – 1)/2]{(1 + 10(h/W)^−0.5 + 0.041[1 – (W/h)]²}

for W/h >> 1. The equation for effective dielectric constant has been generalized in considering only a perfect dielectric constant (with σ = 0 and ω = 0). The influence of frequency on effective permittivity is shown in Eq. 2:

ε_eff (f) = ε_r − (ε_r − ε_eff)/[1 + G(f/f_t)²]   (2)

where

G = [(Z₀ – 5)/60]^0.5 + 0.004Z₀ and f_t = 15.66(Z₀/h) 

with f_t in GHz, h in mils, and Z₀ in Ω.

At higher frequencies, the value of ɛ_eff approaches the value of ɛ_r for a microstrip substrate, implying that most of the energy propagates through the substrate (and less through the air) at higher frequencies. Considering finite metal thickness, Eq. 2 can be rewritten as Eq. 3:

ε′_eff = ε_eff – [(ε_r – 1)/4.6][(t/h)/(W/h)^0.5]   (3)

where t/h ≤ 0.2; 0.1 ≤ W/h ≤ 20; and ε_r ≤ 16. Figure 2 shows the influence of the substrate passivation layer thickness on the effective permittivity, and how variations increase with frequency. High-resistivity silicon substrates with various oxide thicknesses were used in this analysis.              

2. The passivation layer thickness has a determination of the effective permittivity of silicon substrate.

It is important to note that ε_r for a given material is a complex quantity. Equations 4 and 5 represent the complex value of the dielectric constant:

∇ × H = J = J_D + J_C = jωD + J_C = jω[εʹ – jεʺ – j(σ/ω)]E = jωε^*E   (4)

 ε^*  = [εʹ – jεʺ – j(σ/ω)] (complex dielectric constant)    (5) 

for σ = 0, where

Parameter εʹ is known as ac capacitance of the dielectric material; εʺ is the dielectric loss factor and represents dielectric absorption; and δ is the dielectric loss angle associated with molecular motion and relaxation. This relation assumes matter to be linear, having time lag for atomic particles to respond to frequency variations. Furthermore, it shows that the electric and magnetic fields in the dielectric material are no longer in time phase.

The dielectric loss tangent, tan δ, can be shown to equal

tan δ = εʺ/ εʹ

or

tan δ = (εʺ/ εʹ) + (σ/ωεʹ) for dielectric material with high loss.

Frequency variations in the values of εʹ and εʺ depend upon the characteristics of the dielectric material. In the case of a vacuum, εʺ = 0. In the case of a merely good dielectric material, such as polytetrafluoroethylene (PTFE), εʹ is constant and εʺ exhibits a small, incremental increase with frequency. A lossy dielectric material, such as silicon, has a value of εʹ decaying at higher frequencies and considerably larger value of εʺ decaying at RF. In the case of a silicon dielectric material, a loss tangent of 0.005 at 1 GHz increases to 0.015 at 10 GHz, indicating different phenomena than for insulator material, where the overall permittivity decreases with increasing frequency. Considering ɛ₀ as the dielectric constant of a vacuum and A as the capacitive area of a conductor with metal thickness t, the relative dielectric constant, ε_r , can be written as:

ε_r = ε^*/ε₀ = [εʹ − jεʺ - j(σ/ω)]/ε₀ = εʹ_r  − jεʺ = Ct/ε₀A   (6)

Parameter ε_r is frequency dependent, although the variations with frequency tend to be gradual and often fairly constant over a narrow band of frequencies. Variations of the loss tangent, tan δ, with frequency are more pronounced. The imaginary part of Eq. 6 accounts for the damping of the vibrating dipole moments. As shown in Eq. 4, the induced current density for the linear case (J) can be given as:

J = [σ + jω(εʹ − jεʺ)]E = [(σ + ωεʺ) + jωεʹ]E   (7)

The real part of the first term is known as the dissipative current; it is associated with the power loss of a microstrip substrate. The imaginary part of this current is known as reactive current associated with the stored energy. In the case of a semiconductor, it is assumed that the dissipative current is equal to the reactive current density. Dielectric loss is represented by the loss tangent, tan δ, as shown in Eq. 8:

tan δ = (ωεʺ + σ)/ωεʹ = tan δ_d + tan δ_L   (8)

In general, loss tangent term tan δ_L is considered negligible; the only significant loss contributions come from loss tangent term tan δ_d. Loss tangent term tan δ_d results from the polarization loss associated with the intrinsic substrate characteristics, while tan δ_L is defined as the extrinsic loss resulting from the finite conductivity of the substrate material, which is applicable for silicon substrates. The value of the dielectric constant is affected by various other factors, such as temperature and humidity. Table 1 lists variations in loss with frequency for TFG substrate.⁴

A number of approaches are available for measuring the dielectric constant of a material, including the coaxial line method, the resonant cavity method, the Von-Hipple method, the Heston and Smythe method for liquids, the Surber method for liquids, and Poly’s method for high-loss liquids. For stacked substrates, the total permittivity of the structure (ε_T) can be calculated by means of Eq. 9:

ε_T = t_T[(t₁/ε₁) + (t₂/ε₂) + (t₃/ε₃) + …] ⁻¹   (9)

where t_T is the total stacked thickness; t₁, t₂, and t₃ are the thicknesses of the individual substrate layers; and ɛ₁, ɛ₂, and ɛ₃ are the permittivities of those substrate layers, respectively. The wave impedance, Ẑ, can be found by using Eq. 6 to show the following:

Ẑ = [Z₀/(εʹ)^0.5][(cos δ/2 + jsin δ/2)/(1 + tan² δ)^0.25]

Propagation delays affect the performance of high-speed computer logic and high-bit-rate digital communications circuits and systems, and circuit material permittivity plays a role in circuit propagation delays. Considering homogenous and nonmagnetic dielectric media, the propagation delay time per unit length, t_d, is

τ_d (ns/mm) ~ 3.62(ε_r)^0.5   (10)

In CMOS, the gate length is chosen according to the appropriate associated propagation delay. Silicon substrates are not often used for high-frequency applications due to the significant attenuation at high frequencies. The main losses stem from the substrate and surface mode propagation. The low-resistivity silicon substrates used for CMOS processing are not used for RF circuits, since the parasitic EM signal propagation through the substrate causes considerable noise and crosstalk at RF. Crosstalk increases with frequency as a result of substrate coupling effects. Substrate resistance dominates signal propagation performance at moderate frequencies, while the capacitance/permittivity of silicon substrates plays more of a role at higher frequencies.

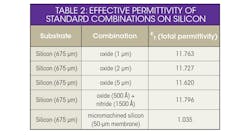
To use silicon substrates at RF and achieve better isolation, crosstalk, and noise suppression, thick oxide layers or isolation structures are usually employed. Silicon-on-insulator (SOI) materials can usually provide good isolation, although with more self-heating effects than standard silicon. Partial SOI materials can be employed, but they require chemical/mechanical polishing. High-resistivity silicon with low doping (using float zone processing) achieves limited isolation at multiple-GHz rates, compromising integration density due to limited junction isolation. In contrast, bulk micromachining allows removal of silicon locally, such as beneath an active device, although this approach leads to fragile device structures and higher radiation losses due to  lower effective permittivity with the removal of silicon material (Table 2).

Working with Silicon                     

CMOS-grade silicon is not considered a good conductor or a good dielectric due to its limited conductivity and resistivity. Through experimentation, however, it was found that silicon material with a thickness of 5 μm above standard grade was sufficiently thick to overcome substrate losses at lower frequencies. The interface above the silicon substrate (typically oxide and nitride layers) is considered as metal-insulator-semiconductor (MIS), as shown in Fig. 3. It supports three modes of propagation: skin-effect mode, dielectric quasi-TEM mode, and slow wave mode. Standard resistivity silicon (ρ ~ 10 to 20 ῼ-cm) supports skin-effect-mode propagation due to its low conductivity.⁵ Higher resistivity silicon ( >1 kῼ-cm) supports quasi-TEM mode propagation, whereas moderate operating frequency and resistivity leads to slow-wave-mode propagation.⁵

3. Micromachining allows the removal of small amounts of silicon beneath active devices for microstrip circuits fabricated on silicon substrates.

Standard resistivity silicon is not suitable for RF applications since the higher operating frequencies result in excessive signal attenuation due to dielectric losses.⁶ Conductor losses are not affected by the substrate resistivity and major loss contributions at RF are from dielectric losses, as well as surface-wave propagation. Free charge carriers cause the main part of the losses in the semiconductor material and, as seen from Eq. 8, the main loss contribution is from the finite conductivity. Employing high resistivity silicon reduces the attenuation, with increase in resistivity by an order of one decreasing attenuation by one-half at C-band frequencies. The functional cutoff frequency for passive circuits is given by:

f_c = 1/(2πρεʺ)

with ρ = 1/(qnµ), where q is the charge concentration, n is the number of half-wavelengths, and µ represents the charge mobility.

The transition frequency of a material, f_c, depends on the resistivity (ρ = 1/σ) which is determined by the doping level of the material. Conductivity is an important semiconductor parameter, depending upon the doping concentration and carrier mobility in contrast to a conductor. Bias also plays an important role in the MIS structure with the introduction of interface losses at the interface between the dielectric (oxide) and the silicon substrate. In addition to substrate losses, losses occur in the depletion, accumulation, and inversion regions.

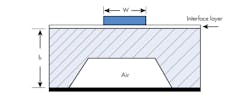
4. This is a depiction of a silicon substrate with an interface layer.

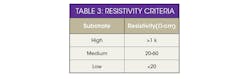
For a silicon substrate, the losses are primarily from the substrate and interface losses occurring between the insulation layer and silicon substrate (Fig. 4). These losses can be minimized by employing a high-quality gate oxide with a high-resistivity silicon substrate. For 10-kΩ-cm resistivity silicon, substrate losses are 0.032 dB/cm, increasing to 32 dB/cm for material with resistivity of 10 ῼ-cm.⁷ Micromachining is generally performed on silicon substrates to minimize losses associated with the substrate. The removal of silicon substrate material by micromachining produces a net decrease in effective permittivity, with a resulting increase in radiation losses (Table 3).

Generally, conductor losses in microstrip are having the major contribution due to skin depth. Skin effect concentrates current near the conductor surface along with edge effects, resulting due to increased resistance. This phenomenon takes place at the frequency at which conductor thickness is higher than the skin depth. The critical frequency at which a conductor makes a transition from electrically thick to electrically thin is

f_crit (Hz) = 4/πμ₀t²   (11)       

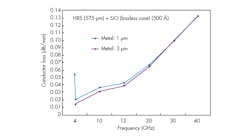
Figure 5 shows the simulated response of the variation of the metallization thickness on the conductor loss on the high resistivity silicon substrate with a 0.5-μm-thick oxide passivation layer. The effect is prominent to 20 GHz but minimized due to skin effect phenomena. This phenomenon also occurs for the transmission lines with width smaller than its thickness, in which the current flows on the sides rather than the top and bottom of the conductor. But in silicon substrate this loss is higher because of the finite metallization thickness due to process constraints.⁸

5. Metallization thickness affects the amount of conductor loss for a silicon substrate.

Compared to standard alumina substrate having attenuation of 5 × 10⁻⁴ (10 GHz), the silicon losses changes with the resistivity considerably. High resistivity silicon substrate (1 k ῼ-cm) is having attenuation of the order of 10⁻³ compared to 10⁻⁴ for silicon with resistivity of 10 kΩ-cm.  Higher-speed devices having pulses with rise time faster than 1 ns, metallization thickness of 10 um makes skin depth comparable with the thickness and cause signal degradation. Conductor attenuation (α_c) can be described as:

α_c = 0.072[(f)^0.5/wZ₀]λ_g (dB)/λ_g

= (8.686/wZ₀)(πfμ/σ)^0.5 (dB)/m   (12)

where f is in GHz.

In terms of quality factor, conductor attenuation is:       

α_c = 8.68βn/Q_u (dB/mm)   (13)

where Q_u = Q_L/(1 – 10^−(IL/20))

where β_n = 2π/l_g and n is the number of half-wavelengths.

The quality factor associated with the attenuation constant, Q_c, can be written as:

Q_c = 27.3/α_c ≈ 0.63h(σf)^0.5 (in GHz)                     

The dielectric attenuation constant attached with the loss can be expressed^{9, 10} as:

α_s = 27.3[ε_r(ε_eff – 1)tan δ]/[ε_eff(ε_r – 1)][(tan δ)/λ_g]  in dB/λ_g   (14)

where

λ_{g =} λ₀/(ε_eff)^0.5                    

The total attenuation can be written as α = α_c + α_s. For silicon, the total attenuation is α = −α_c + α_L +

α_d. The quality factor associated with the attenuation constant, Q_s, can be written¹ as:

Q_s =  27.3/α_s ≈ 1/(tan δ_d + tan δ_L);

1/Q = 1/Qc + 1/Q_S;

Q = (β/2α)([λ₀(α_c + α_s)]/{π[ε_eff (f)]^0.5})

tan δ = tan δ_d + tan δ_L = ε_eff(ε_r – 1)/[Q_sε_r(ε_eff – 1)]

The power radiated from any discontinuity can be modelled as shunt conductance, G_rad :

G_rad = (60π²/Z₀²)(h/λ₀)² ((8/3ε_eff)[1 + (4/5ε_eff) – (1/ε_r)] + …)

The radiation becomes significant at higher frequencies according to the relationship:

fh >2.14(ε_r)^0.25

where f is in GHz and h is in millimeters.

High-resistivity silicon with a 5-μm oxide layer deposited by plasma-enhanced chemical vapor deposition (PECVD) has higher attenuation for microstrip than standard alumina substrates (about 0.06 dB/mm), although somewhat less than the 1 dB/mm attenuation in microstrip lines on standard silicon substrates characterized at X-band frequencies.

Propagation of surface waves in the dielectric material contribute to the overall attenuation in microstrip lines. A dielectric sheet on a ground plane acts as a guiding structure for surface waves.¹¹ The electric field at the bottom surface is considerably high, which leads to the excitation of the substrate mode. The waves may propagate in any direction parallel to the surface. Transverse-magnetic (TM) mode, which is the lowest-order mode with no cutoff frequency, will propagate to DC, but is weakly guided by the surface. Since the propagation coefficients for this surface-wave mode and the normal microstrip quasi-TEM mode are different, coupling between the modes is negligible. At lower frequencies, the majority of energy is transmitted above the substrate so that ɛ_eff ~ 1. At higher frequencies, ɛ_eff for the surface wave increases, resulting in coupling between the modes resulting in comparable phase coefficients. The lowest frequency, f_L, at which coupling to a surface-wave mode may occur, is:

f_L = c arctan(ε_r)/πh[2(ε_r – 1)]^0.5   (15)

To avoid surface-wave propagation, microstrip circuits are operated below f_L. The phenomena is predominant for narrow microstrip lines; for wider microstrip lines, transverse microstrip resonance may occur, which can also be suppressed by the use of narrow longitudinal slots in the metal strip.

Silicon is a low-cost substrate material with potential for RF/microwave microstrip circuits, provided that the loss mechanisms of the circuit structures are fully understood. Substrate permittivity is a complex parameter that has a huge impact on microstrip on silicon loss mechanisms, but it is a parameter that has been thoroughly analyzed, with much information available.

Accurate dielectric properties, including dielectric constant and intrinsic dielectric loss tangent, are essential for designing microwave integrated circuits on silicon. Along with the above, present-day circuits having RFIC and RFCMOS concept on silicon need accurate prediction of the losses associated with the substrate to reduce the turnaround time in multiple iterations.

Kamaljeet Singh, Scientist/Engineer, Systems Engineering Group

A.V. Nirmal, Group Director, Systems Engineering Group

S.V. Sharma, Deputy Director

ISRO Satellite Centre, Bangalore, India

Acknowledgment

The authors gratefully acknowledge the director of ISAC for his support and encouragement.

References

1. S.Y. Liao, Microwave Devices and Circuits, Prentice Hall, Englewood Cliffs, NJ. 

2. David M. Pozar, Microwave Engineering, 2^nd ed., John Wiley & Sons, New York, 1998.

3. T.C. Edwards, Foundations for Microstrip Circuit Design, John Wiley & Sons, New York, 1991.

4. L. Mruthyunja and K.N. Suryanarayana Rao, “Measurement of dielectric constant of aerospace dielectric materials,” Journal of Spacecraft Technology, Vol. 6, No. 2, 1996, pp. 28-31.

5. Kamal Benaissa, J.-Y. Yang, D. Crenshaw, S. Sridhar, et al. “RF CMOS on high resistivity substrates for system-on-chip applications,” IEEE Transactions on Electronic Devices, Vol, 50,  No. 3, March 2003, pp. 567-576.

6. R.-Y. Yang, C.-Y. Hung, Y.-K. Su, M.-H. Weng, and H.-W. Wu, “Loss characteristics of silicon substrate with different resistivities,” Microwave and Optical Technology Letters, Vol. 48, No. 9, September 2006, pp. 1,773-1,776.

7. C. Schollhorn, W. Zhao, M. Morschbach, and E. Kasper, “Attenuation Mechanisms of Aluminum Millimeter-Wave Coplanar Waveguide on Silicon,” IEEE Transactions on Electron Devices, Vol. 50, No. 3, March 2003, pp. 740-746.

8. James C. Rautio, “An investigation of microstrip conductor loss,” IEEE Microwave Magazine, December 2000, pp. 60-67.

9. Ramesh Garg and K. C. Gupta, Computer-Aided Design of Microstrip Circuits, Artech House, Norwood, MA, 1981.

10. Panagiotis Sarafis, Emmanouel Hourdakis, and Androula G. Nassiopoulou, “Dielectric Permittivity of Porous Si for Use as Substrate Material in Si-Integrated RF,” IEEE Transactions on Electronic Devices, Vol, 60, No. 4, April 2013, pp. 1,436-1,443.

11. E.H. Fooks and R.A. Zakarevicius, Microwave Engineering Using Microstrip Circuits, Prentice-Hall, Englewood Cliffs, NJ.