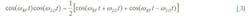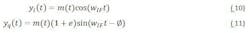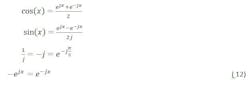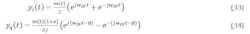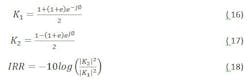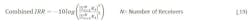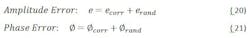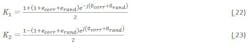Receiver Design Considerations in Digital Beamforming Phased Arrays
Download this article in .PDF format
This file type includes high resolution graphics and schematics when applicable.
Introduction
Digital beamforming phased arrays are becoming an increasingly common antenna product both for defense and commercial applications. The primary technological advancement making this possible is the development of high performance miniaturized and highly integrated receivers. Much literature exists on receiver design as a single entity. This tutorial is intended to summarize the collection of receiver design considerations with emphasis on impact to the digital beam-forming phased array application.
The subject is approached by first describing distributed receiver correlated versus uncorrelated errors that historically have not been considered for systems with a single centralized receiver. This is followed by a detailed evaluation of both a direct conversion receiver and a super-heterodyne receiver. Channel pair cancellation is introduced and is directly related to the ability to form nulls in the antenna pattern. The concluding section contains some additional receiver terms for completeness.
Digital Beamforming Application Overview
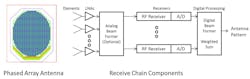
The digital beam-forming concept is shown in Fig. 1. The phased-array antenna is made up of many elements and many receivers. The number of receivers may be less than the number of elements. An “every element” system is defined as having a receiver for every element. In many cases this becomes impractical due to size or power constraints. For these cases, an analog beam-former is used before the receivers. The analog beam-former could be power combining of several elements or a weighted sum of overlapped elements. The receivers convert the RF frequency to a digital output. Processing is performed to compute the antenna pattern and numerous patterns can be processed simultaneously.
Many references exist on digital beam-forming methods and antenna design. The scope of this discussion is to summarize considerations for the receiver design in this application.
Correlated Versus Uncorrelated Error Terms
A digital beam-forming system sums weighted versions of every receiver output to form antenna patterns. A calibration is performed to ensure the desired signals add coherently. A system concern is the effect of receiver errors through the digital beam-forming process.
Consider the sum of two error voltage terms, written as:
Error terms that are uncorrelated (c = 0) reduce by l0logN, where N is the number of receiver channels. Correlated errors (c = 1) add coherently across the array and do not reduce at the system level. If an error term is perfectly matched across all the receivers, the system error will be the same as the individual receiver error. Thus, tracking of correlated and uncorrelated error terms in the system is a primary concern.
As each error term is evaluated, it can be broken down into correlated and uncorrelated components:
Mixer Spurious Components
A mixer is a form of analog multiplication. The intention is to reduce the received RF frequency to a lower frequency by multiplication with an LO. An ideal frequency translation would be:
In receiver design, great care is taken in frequency planning to avoid in-band spurious. For digital beamforming, the frequency planning effort remains, however an additional consideration is ensuring the spurious signals are decorrelated across the array of receivers. A proven method to ensure mixer spurious decorrelate is to add a phase shifter in the LO path and provide a digitally controlled random LO phase across the array.6 Consider the cosine multiplication of a particular harmonic as:
Filtering the harmonic leaves the in-band spur of:
The calibration is on the primary signal when n = m = 1, and the phase shift ɸ is removed. For the mth harmonic the spur is rotated an additional amount m. The method requires phase shift control of a complete 360-deg. range but does not require great phase shift accuracy.
Distributed PLL Considerations
A method to distribute LO frequencies to all the receivers is necessary. This could be a centrallized LO, a distributed LO generated locally at every receiver, or an in-between approach with an LO generated for some number of receivers.
A centralized LO distributed to all the receivers will provide a common reference to all the receivers. However the LO noise will also be a correlated noise source across the array. To achieve the noise benefit of combined receivers the LO noise must be 10logN better than a single receiver where N is the number of elements.
A distributed LO relaxes the noise requirements for the LO generation, but comes with some additional considerations. A reference is still needed and must be distributed to the LO generation circuit—although the reference is typically at a lower frequency, which is easier to distribute. All the distributed LOs maintain their relative phase across the array at the completion of the antenna calibration. If this is not maintained, the calibration to align all the receivers is no longer valid. This requirement can limit the options of implementation methods for distributed LO generation. In theory, a distributed integer N PLL can achieve this, but absolute phase errors need to be specified for the application; if the PLL output is used for any digital clocks, no cycle slips can be tolerated from the PLL.
The Direct Conversion Receiver
Direct conversion receivers, also known as Zero-IF or homodyne receivers, offer significant advantages in implementation for a wideband receiver. Complications in direct conversion receivers are well documented, and include LO leakage, in-band IF harmonics, and the IQ image.
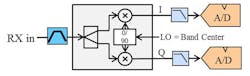
A block diagram of a direct conversion receiver is shown in Fig. 3. The input RF signal is mixed with two LO signals that are identical in frequency, but 90 deg. out of phase. This mixing scheme is called a quadrature demodulator and creates the I/Q channels directly that are then sampled by two A/D converters.
In-Band LO Concerns
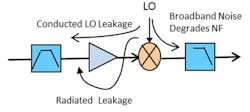
In a direct conversion receiver the LO is in the center of the received band. In any mixing system there are practical isolation limits. Mixers specify the isolation among their ports. There are several conducted and radiated isolation paths of concern for a direct conversion receiver. Each one will be systematically evaluated.
The first concern is LO energy radiated out of the receive antenna. The LO will conduct to the RF port at a level based on the LO power level and the mixer LO to RF isolation. This unwanted energy will continue toward the radiating element based on the S12 of each component. Since the LO is in the operating band, there is no additional filtering to help suppress this signal. In a phased array, power will be radiated back into the air at a sum of the LO leakage from all the receivers. The energy likely will not correlate due to provisions for spur decorrelation; however, it will non-coherently sum to a broad antenna pattern of radiated energy. The concern for this term depends on the system specifications for radiated power during receive.
Some amount of LO energy can will be radiated to the front of the LNA. The severity of this leakage path depends on the circuit layout. This can also result in radiated LO power, but the primary concern for this path is that it can be amplified by the LNA, increased in power and delivered to the mixer similar to any other receive signal. Once in the mixer, this will mix to a DC term at the IF port.
An in-band LO can also degrade the noise figure contribution of the mixer. The LO will have a sideband noise level that needs to be considered. This noise will appear at the RF and IF ports on the mixer attenuated by the LO to RF and IF isolation. This noise can be above thermal noise in many cases and becomes an additional term degrading mixer noise figure.
The leakage paths above are discussed in many of the references. An additional area for phased arrays not widely discussed is conducted leakage degrading channel to channel isolation. Just as the LO can conduct through reverse isolation to the radiating element, the RF from one channel can conduct to other channels through the LO distribution. Filtering available in heterodyne receivers can alleviate this problem but, in a direct conversion phased array, reverse isolation of distribution components should be compatible with channel to channel isolation requirements.
IP2
IP2 can be a dominant concern in direct conversion receivers. The second and third order distortion terms can be modelled as:
The concern with second order distortion is any input signal whether in band or out of band the gets into the mixer will down-convert to DC. This can be seen observing a cos2 identity.
Image Rejection
The IQ image is formed from amplitude and phase errors in the quadrature demodulators and is also well documented. For a phased array, distributed digital beam-forming architecture, the dominant concern with the IQ image is to develop a method that will ensure the image term decorrelates. Decorellation of the IQ image will allow 10logN improvement through beamforming gain in a manner similar to noise terms.
The ideal output of the quadrature demodulator is:
Identities used in the next derivation include:
The term ejWIFt represents the primary signal and the term e-jWIFt represents the image.
The complete baseband signal can now be rewritten as:
The term e-jπ/2 can be ignored as a constant phase shift. The primary signal terms can be assigned K1 and the image signal K2, and the magnitude of the image defined as an image reject ratio(IRR).
Image Reject Ratio as a function of amplitude and phase are are shown in Fig. 5. Practical limitations in the analog circuitry typically limit the image rejection ratio to ~40dB. Digital corrections can be applied and some analyses have claimed image reject ratio improved toward 60 dB.
The above image rejection analysis is not new. The advancement will come in using the analysis to develop a method to ensure IQ image is not correlated across an array of receivers.
Equations 12 and 13 track the error terms of the primary signal and the image in a form that allows coherent addition. Through beam-forming the terms can be coherently added to form a combined image rejection ratio as:
To consider the effect in summing K1 and K2, consider breaking the error terms further into terms that are common (or correlated) across the receivers, and terms that are random across the receivers:
K1 and K2 can now be expanded to:
Through addition of K1 and K2 across many receivers, the random terms will decorrelate and their contribution will approach zero. However, the correlated amplitude or phase error terms will remain and dominate the Combined Image Rejection Ratio.
The error terms begin with analog errors in the quadrature demodulator. If these errors can be made truly random, then a 10logN benefit should be realized through digital beam-forming gain. Through mass production of the RFICs, it seems highly likely the analog errors will be consistent and thus correlated across the receivers. If the assumption of consistency in the RFICs is correct, efforts to improve analog circuitry may yield little benefit in a distributed system.
A digital error correction appears as a viable method to remove the correlated errors. In general a digital correction will improve the IQ image to within SNR limits of the measurements. The calibration limitations are from noise and thus random. Therefore if the output of the digital correction is truly random across the receivers, then a 10logN benefit could be realized in addition to the improvement of a single receiver.
LO Quadrature Generation
A common method for generation of the LO frequencies (the 0- and 90-deg. LO signals to the mixers) is to use a digital frequency divider and tap different nodes within the latch circuits. Digital frequency dividers can be made easily, with very low noise, very broadband, and a high upper frequency limit. The quadrature accuracy is also very good because the nodes tapped are digital and controlled by the clocks to the divider. The concern with this method of quadrature generation is that if the LO is interrupted during the frequency transition, the divider will reset and come up in one of two possible phase states.
This problem requires careful coordination with the LO synthesizer design to ensure all dividers remain in sync, or coordination with the system level calibration to provide a method for a rapid calibration during this situation. The frequency divider method also requires an input at twice the LO frequency and is another consideration for impact in the synthesizer design.
An alternate method is to provide a quadrature phase shifter. This method is analog and does not have any startup concerns; the input frequency is the LO frequency used by the mixers. The compromise with this method could be additional noise and limited broadband accuracy depending on the specific method chosen.
Operation at DC
Many errors result in a DC term. The IP2 term any frequency into the mixer results in DC. LO leakage into the receive path self-mixes with the LO and creates DC. One noise consideration is that flicker noise in the IF chain follows a 1/f curve, causing the overall noise to be higher for any near DC reception. For these reasons many direct-conversion systems implement a DC null. This could be with a capacitive coupled highpass filter, or a control loop to remove the DC bias.
Another concern is any two signals closely spaced and separated by âf in frequency that get to the mixer will mix together to create a baseband signal at âf.
The Super-Heterodyne Receiver
When the disadvantages described for the direct conversion architecture cannot be overcome to meet the system specifications, an alternate method is needed. The superheterodyne receiver mitigates every problem previously discussed with direct conversion. The expense paid is added complexity. There are times, however, when the added complexity is worth the price in order to achieve the performance objectives.
The super-heterodyne receiver dates back to a 1918 invention by Edwin Armstrong.14,15 The term "heterodyning" sounds impressive, but is just the concept of mixing two signals together to create a lower beat frequency. In Armstrong’s concept the incoming RF is mixed with an LO to a lower intermediate frequency (IF). This intermediate frequency is filtered and sent to a detection circuit to extract the modulated information signal. Numerous variations and improvements have been made over the years, and this architecture became the standard for almost all radio and television receivers in the 20th Century.
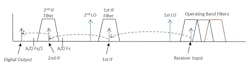
Figure 6 shows a high end super-heterodyne architecture. The variation shown is a dual down-conversion type with many features desirable in a high performance receiver. It is worth considering this implementation, the functions of each component, and the frequency plan impact. Once the approach is understood, components unnecessary in particular receiver design and requirements can be removed.
The RF path starts with a filter bank consisting of overlapped filters covering the operating band. This frequency is mixed to an intermediate frequency and filtered. The intermediate frequency is chosen high enough that image rejection can be provided by the front end RF filters. When the intermediate frequency is too high to sample in the A/D directly an additional down-conversion is added to produce a 2nd intermediate frequency. An antialiasing filter is provided prior to A/D sampling. Gain control is provided at every frequency to allow programmable optimization of gain, noise figure (NF), and the input third order intercept (ITOI).
Additional low pass filters are provided before every mixer to ensure the amplifier harmonics do not dominate the mixer spurious. Low pass filters are provided after every mixer to filter the image helping relax the ultimate broadband rejection of the band-pass filter. Limiting protection is provided prior to the LNA and protection is also provided before the A/D to prevent damage if the final amplifier saturates.
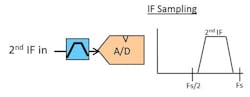
Early in the receiver design the A/D operation is chosen. Sampling in the 2nd Nyquist zone has become popular. The primary benefits are that the 2nd IF harmonics produced either in the mixer or in amplifier non-linearities are out of band and can be filtered. Sampling in a higher Nyquist zone produces a digital downconversion and can be quite useful when frequency planning. The primary compromise of IF sampling is the A/D performance degrades as the input frequency increases. This concern must be balanced with other tradeoffs in the overall receiver design.
Figure 8 shows an example frequency translation diagram. An operating band filter is selected, the input mixes with the 1st LO to produce a signal in the IF filter range. The 1st IF mixes to with the 2nd LO to create the 2nd IF which is sampled and creates the digital output.
A single downconversion could also be considered. Considerations for this option include sample rate required from the data converters balanced with adequate image rejection in the downconversion.
As a general statement, a properly designed superheterodyne receiver will have far superior sensitivity and immunity to interference when compared to a direct conversion receiver. For a phased array digital beam-forming the challenge becomes size, power, and cost constraints when many receivers are needed across the array.
Channel Pair Cancellation Ratio
In modern digital beam-forming antennas, the ability to create nulls in the antenna pattern has increased importance for operation in high interference environments. The depth of the nulls in limited by error terms in the antenna receivers. Channel Pair Cancellation Ratio (CPCR) has been established as the system level performance metric in this area.
CPCR is a measure of how well a common input signal can be cancelled between receivers. It represents how well the receivers can be matched after equalization. CPCR can be defined as an input jamming-to-noise ratio divided by an output jamming-to-noise ratio.
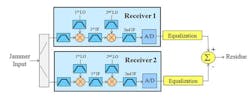
CPCR can be conceptualized as shown in Fig. 9. In this example a dual down conversion receiver is shown. The equalizer is calculated during the calibration process and is intended to match the two receivers. A common RF input signal is injected into both receivers. The 2nd IF signal is digitized by the A/Ds and run through an equalizer. One equalization output is subtracted from the other and a residue remains. This residue left over is due to mismatches in the receivers. The residue relative to the input signal is in effect the CPCR between the two receivers.
9. CPCR residue.
It should be noted that until this point our goal was to ensure all errors were uncorrelated across the array. CPCR has the opposite objective. Correlated errors will cancel; uncorrelated errors will not. Some of the hardware errors limiting CPCR performance are referenced in ref. 8.
Additional Receiver Parameters
Sensitivity
Receiver sensitivity is a system metric given to any receiver. It is generally the minimum signal level detectable with some probability of detection. The value is a function of the receiver noise figure and gain, the modulation bandwidth (and thus the noise bandwidth), the processing gain of the waveform, and the integration gain (if multiple pulses are integrated). During the specification and component parameter allocation stage of the receiver design, the parameters for receiver sensitivity in system should be clearly defined.
Out-of-Band Blocking
Immunity to out of band interference is a critical performance metric for any receiver. Typically one may think of measurable frequencies ending up in band somewhere in the receive chain. An alternate metric proposed in ref. 20 is a measure of compression in the front end of the receiver. Even if the filters reject the interference somewhere in the receive chain, a large interference signal can saturate the receiver front end and alter the receive gain in small amounts of a percentage of a dB. This could seem harmless, but with a pulsed interferer, gain changes in the receiver can result in a measurable modulation on the carrier.
Cascaded Analysis
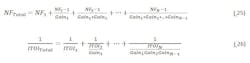
As specifications are flowed to the receiver, cascaded gain, noise figure, ITOI budgets are tracked to the components in the receiver chain. The cascaded noise figure and ITOI equations are included for the sake of completion.
Conclusion
Receiver design in the form of individual receivers is well documented, and has become an established art. The area for further growth and maturity is the effect of numerous receivers summed in an array. This tutorial has compiled a summary of considerations for receiver design and presented considerations when used in a digital beam-forming phased array application.
Peter Delos is lead RF/RFIC engineer for Lockheed Martin Corp.
References
1. Abidi, “Direct-Conversion Radio Transceivers for Digital Communications,” IEEE, 1995.
2. Razavi, “Design Considerations for Direct-Conversion Receivers,” IEEE, 1997.
3. Rudell, “Frequency Translation Techniques for High-Integration High Selectivity Multi-Standard Wireless Communication Systems,” Ph.D. thesis, University of California, Berkeley, 2000.
4. G. Vallant, et al., “Analog IQ Impairments in Zero-IF Radar Receivers: Analysis, Measurements and Digital Compensation,” IEEE, 2012.
5. L.C. Howard, N.K. Simon, and D.J. Rabideau, “Mitigation of Correlated Non-Linearities in Digital Phased Arrays Using Channel-Dependent Phase Shifts,” IEEE Int. Microwave Symp., 2003.
6. L.C. Howard, D.J. Rabideau, “Correlation of Nonlinear Distortion in Digital Phased Arrays: Measurement and Mitigation,” IEEE Int. Microwave Symp., 2002.
7. K.C. Lauritzen, et al. “Impact of Decorrelation Techniques on Sampling Noise in Radio-Frequency Applications,” IEEE Trans. on Inst. and Meas., Vol. 59, No. 9, Sep. 2010.
8. Lauritzen, Krichene, and Talisa, “Hardware Limitations of Receiver Channel Pair Cancellation Ratio,” IEEE Transactions of Aerospace and Electronic Systems, Jan 2012.
9. McClaning, Vito, “Radio Receiver Design,” New York, Noble Publishing, 2000.
10. Cook and Bernfeld, “Radar Signals, An Introductory to Theory and Application,” New York, Academic Press, 1967.
11. Skolnick, “Radar Handbook,” New York, McGraw Hill, 1978.
12. Stimson, “Introduction to Airborne Radar,” SciTech Publishing, 1998.
13. Barton, “Modern Radar System Analysis,” Norwood, MA, Artech House, 1988
14. L. Lessing, Man of High Fidelity: Edwin Howard Armstrong, A Biography, New York: Banton Books, 1969.
15. Microwaves101.com, “Superheterodyne Receivers,” 2012.
16. Microwaves101.com, “Receiver Sensitivity.”
17. K.C. Lauritzen, et al. “High Dynamic Range Receivers for Digital Beamforming Radar Systems,” IEEE, 2007.
18. Henderson, “Mixers in Microwave Systems,” WJ Tech-Note, 1990.
19. Stuetzle, “ Understanding IP2 and IP3 Issues in Direct Conversion Receivers for WCDMA Wide Area Basestations,” Linear Technology Application Note, 2008
20. V. Gregers-Hansen, “Radar Dynamic Range Specification Measurement”, Radar Conference - Surveillance for a Safer World, 2009. RADAR. International, October 2009