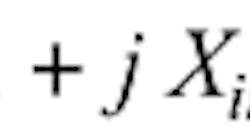Transmission-line transformers (TLTs) provide broadband impedance transformation in a wide variety of RF circuits. When using TLTs, analysis of the frequency response is an important consideration.1,2 Such analyses usually assume that the load and source are impedance matched through the transformer, although this is not always the case.
At times, matching between the primary and secondary impedances of a TLT is either impractical or undesirable. An example of this is the interface circuit between a photodiode and an amplifier used in a particular optical receiver architecture. Based on this example, Guanella and Ruthroff TLTs were analyzed, although TLTs are useful in many applications.
A number of architectures are used for optical receivers.3 This article concerns a special case (Fig. 1) with a broadband 75-Ω power amplifier. The design challenge is to find an interface circuit for optimal system sensitivity without degrading the system bandwidth and amplitude flatness.
From the viewpoint of the RF circuitry, the photodetector can be modeled as a current source with a high source impedance. When the resistors used for the DC bias are taken into account, the photodetector and bias circuit can be modeled as a current source with a source impedance on the order of kiloohms. On the amplifier side, it can be replaced by a load impedance, RL, which is equal to its input impedance, RA. This reduces Fig. 1 to the equivalent circuit shown in Fig. 2. The load and source impedances are chosen as 75 Ω and 2 kΩ, respectively, for the purposes of numerical analysis. TLTs are often selected as the interface in such cases when wide bandwidths are required.
From a power-transfer consideration alone, a stepdown transformer that matches RL (75 Ω) to Rs (2 kΩ) would deliver maximum system responsivity. However, such a high-ratio impedance transformation (26:1) is not only difficult to implement but results in an unacceptable reduction in bandwidth due to the photodiode's parasitic capacitance. As a compromise, a 4:1 TLT can provide enough gain and bandwidth, even though it will result in a condition of mismatched impedances.
A TLT generally has a reactive component and exhibits frequency-dependent operation. Thus, the transformed impedance Zin, seen from the diode side as defined in Fig. 2, can be expressed in general as:
Assuming a lossless transformer, power dissipated in the real part of Zin, denoted as Pin, is equal to that in RL, which in turn is proportional to the system responsivity. A simple circuit calculation shows that:
Thus, through Eq. 1, the issue of frequency dependence of the system responsivity is reduced to finding Zin as a function of frequency.
In a TLT, parasitic effects are greatly suppressed because most stray capacitance is absorbed by the line inductance to form the characteristic impedance of the transmission line. This suppression of parasitic effects is the main reason that TLTs have higher frequency limits than conventional transformers. Although in some applications the ultimate high-frequency limit is set by the residual parasitic effects, this article will consider only the frequency response due to the intrinsic circuit parameters such as the length and characteristic impedance of the transmission line and load and source impedances. As part of this idealized analysis, the TLT is considered lossless and free of parasitic effects. Furthermore, to get an insight on how the frequency dependence arises, two conditions are listed below.1 When these conditions are met, a TLT is considered ideal in that it has a frequency independent response regardless of the circuit parameters.
1. Only odd mode excitation is allowed, i.e. the currents in the conductors making up the transmission line are in opposite directions. High-permeability toroids are employed in many TLTs for this purpose.
2. The transmission line is short compared with the wavelength (say, less than l/8), which leads to a situation in which the voltages at two ends of a transmission line are the same and the currents at each end of an individual conductor are equal.
Validity of the first condition usually sets a low-frequency limit on the ideal TLT, while validity of the second condition sets the high-frequency limit on the ideal TLT.
For two types of TLTs, Guanella and Ruthroff, the analysis is first performed under these ideal conditions and then focused on the non-ideal situation at high frequencies.
Figure 3 shows a Guanella transformer. Essentially, it consists of two pairs of transmission lines that are connected in series at the high-impedance side (the input in this case) and in parallel at the low-impedance side (the output). The assignments of the voltage and current on the transmission lines, Vi and Ii, are only correct for the two ideal conditions mentioned earlier, and under these conditions the following relationships can be easily established:
The series connection at the input leads to Vin = 2Vi and Iin = Ii. The parallel connection at the output leads to Vout = Vi and Iout = 2Ii. Therefore,
Then Rin = 4 Rout, confirming the 4:1 impedance transformation ratio and the frequency independency. When the length of the transmission line becomes relatively long, the second condition is no longer valid and modifications are needed.
In Fig. 3, the input impedance Zin is simply the sum of two serial impedances transformed from the same load through two identical pairs of transmission lines respectively (true only when the first ideal condition holds). These two impedances are obviously identical and designated as ZL'. Because they are identical, an analysis on the impedance transformation through one pair of transmission lines is sufficient.
In this configuration, the current through load ZL is the sum of currents from each pair and therefore is twice that from a single pair. Hence, if a single TLT is used for analysis, the equivalent load should be doubled from the real value of ZL to give the same current and voltage at the load. The pertinent equation for ZL' can be found in any textbook on microwave engineering:
where:
ZL = the load impedance (in Fig. 2),
Zc = the characteristic impedance of the transmission line, and
bl = the phase angle.
From Eq. 2, the frequency dependence of Zin (=2ZL') is solely through the phase angle bl when ZL is purely resistive. Numerical results using Eq. 1 and 2 for several values of Zc and Rs=2 kΩ, RL=75 Ω are shown in Fig. 4. The normalized power P(bl)/P(0) in logarithmic scale is used in the plot, where P(0) is the low frequency limit of P(bl) and given by:
The plot shows that the curve for Zc=2RL=150 Ω is flat, indicating that it is not dependent on frequency. This can be easily concluded by examining Eq. 2. Also, the condition for perfect flatness is independent of the source impedance, Rs.
Page Title
Figure 5 shows the circuit schematic of another popular 4:1 transmission line transformer, the Ruthroff transformer. Unlike the Guanella TLT, which requires two pairs of transmission lines, a 4:1 impedance transformation can be achieved with a single transmission line in the Ruthroff topology. For the case when a balanced-to-balanced (with a center ground tab) impedance transformation is required, however, two parallel pairs of transmission lines are still needed. The single and two-TLT Ruthroff configurations are shown in the inserts in Fig. 6 and 7, respectively. It is evident that an analysis of the single-TLT configuration is sufficient.
Under ideal conditions, voltages and currents at input and output ends are:
and therefore Vin/Iin = 4(Vout/Iout), indicating a 4:1 impedance transformation.
When the transmission line is long, voltages V1 and V2 and currents I1 and I2 are related through:
where V+ and V− are forward and backward traveling waves at port 2, respectively. Solving Eqs. 3 through 6 gives V1 and I1 expressed in terms of V2, I2, and the transmission-line parameters, Zc and bl:
In addition,
Using Eqs. 7 through 11, after some algebra, the input impedance Zin is:
Figures 6 and 7 show plots of numerical results for single and two-TLT configurations, respectively, for Rs = 2 kΩ, RL = 75 Ω, and Zc as a variable. As shown in the insert of Fig. 7, for the two-TLT configuration the actual values for Rs and RL used in Eq. 12 are 1 kΩ and 37.5 Ω, respectively, to account for the fact that Eq. 12 is for the single-TLT configuration. A close comparison of two groups of curves in Figs. 6 and 7 reveals that the curve with a Zc in the single-TLT configuration is identical to that with 2Zc in the two-TLT configuration. In fact, this can be readily seen from Eq. 12, since RL used in the two-TLT configuration is simply one-half that in the single-TLT configuration. This feature is of significance in practical design because a TLT with high Zc is often difficult to realize in practice.
The following can be concluded:
- Even with a limited number of curves plotted in Figs. 4, 6, and 7, one can see that the frequency response curves are greatly affected by the choice of Zc, ZL, and Zs. For the 4:1 Guanella transformer there is a condition (Zc =2ZL) for which the response is completely frequency independent whereas the frequency response of the 4:1 Ruthroff transformer always starts to roll off at certain frequency point.
- It has been assumed that transmission lines are lossless, aslthough in reality they exhibit loss. As shown in Figs. 4, 6, and 7, for both types of TLT when Zc is chosen properly the response curve increases with frequency up to a certain point (around βl=1.5). This feature can be utilized in practice to compensate the loss in the transmission line and can it also provide system gain with an upward slope.
- The frequency response of the Ruthroff transformer monotonically decreases at high frequencies, while the Guanella's response is periodic with frequency.
- For the load and source impedances considered in this article, the Ruthroff transformer with the two-TLT configuration requires the lowest Zc to have an upward response curve. The approach also supports differential operation, but usually requires two parallel toroidal transformers.
ACKNOWLEDGMENT
The authors would like to thank Dr. Derald O. Cummings for introducing some basic concepts and techniques on the subject at the early stage of this project.
REFERENCES
- W. Alan Davis and Krishna K. Agarwal, Radio Frequency Circuit Design, Wiley, New York, 2001.
- Jerry Sevick, Transmission Line Transformers, 4th Ed., Noble Publishing, Norcross, GA, 2001.
- Stephen B. Alexander, Optical Communication Receiver Design, Bellingham, SPIE Optical Engineering Press, San Jose, CA, 1997.