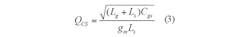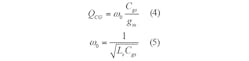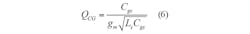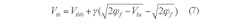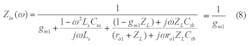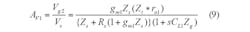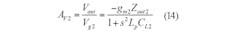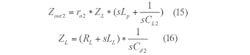CMOS LNA Aids UWB Receivers

A number of UWB LNAs have been developed based on CMOS technology.^2-8 The distributed amplifier (DA) has been one of the more popular architectures for this application. Since DA LNAs provide good wideband input matching, flat gain, and generally high input third-order intercept (IIP3) performance, they are well suited to these UWB applications.^2-4 But DA LNAs consume a great deal of power with relatively low power gain in a large chip area.

Resistive feedback is a good solution for obtaining wide bandwidth and flat power gain.^5-7 However, the use of a resistor in the feedback path reduces the power gain and degrades noise performance. One recent LNA topology of note is the cascode configuration with a Chebyshev input matching filter, which provides good wideband input matching and high power gain⁸; however, the noise figure is degraded by the filter’s insertion loss.

One challenge for UWB LNAs is posed by the linearity requirements, owing to the large numbers of in-band interference sources in that frequency range and the cross-modulation/intermodulation caused by blockers or transmitter leakage in a reconfigurable receiver.⁹ Furthermore, while the transmit frequency (f_T) increases with technology scaling, linearity tends to degrade due to lower supply voltages in use and high-field mobility effects.⁹ This makes wideband linearization important.^10,11

Linearization techniques which optimize overdrive voltage (V_gs - V_th) can be used to obtain peak IIP3. However, the bias voltage range for peak IIP3 is narrow, so that boosting linearity can be sensitive to process variations. The derivative super-position (DS) method^12-14 uses an additional transistor’s nonlinearity to cancel that of the main device; it involves MOS transistors working in triode¹² or in the weak inversion region^13,14.

Therefore, using the DS method, it is difficult to match the transistors working in different regions, resulting in a linearity improvements that are highly sensitive to variations in pressure volume and temperature (PVT). The body biasing technique¹⁵ is suitable for improving linearity performance; unfortunately, it degrades gain and noise performances. In ref. 16, the post-distortion technique was used to improve linearity, with good results.

To achieve good performance for UWB systems, a common-gate (CG) LNA design is proposed. These LNAs offer simple input matching networks with good linearity and low power consumption compared to common-source (CS) LNAs. Because the power gain of a CS LNA tends to be low,¹⁷ a CS amplifier is used in this design as a second stage. The proposed LNA design employs current-reuse and forward body biasing techniques to achieve low power consumption. In addition, shunt-series peaking techniques are used to extend the 3-dB bandwidth, and a post-distortion technique is employed to improve the linearity performance.

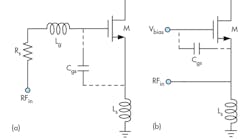
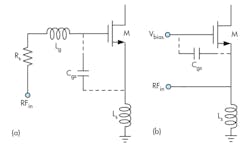
Based on their input matching characteristics, reported CMOS UWB LNA architectures can be divided into two major groups: CS and CG LNAs.¹⁸Figure 1 offers the two general topologies for these amplifier types. Figure 1(a) is a CS LNA that requires at least two inductors (L_g and L_s) for simultaneous noise and input matching (SNIM). Assuming the channel resistance, γ₀, and the gate-drain parasitic capacitance, C_gd, are negligible, the CS LNA’s quality factor (Q) can be derived as:

Substituting Eq. 2 into Eq. 1 yields Eq. 3:

where:

ω₀ = the resonant angular frequency of the input impedance;

g_m = the transconductance of the metal-oxide-semiconductor field-effect transistor (MOSFET);

L_g = the gate inductor;

L_s = the source inductor; and

C_gs = the gate-source parasitic capacitance of the device.

By substituting Eq. 5 into Eq. 4, Q_CG can be expressed by Eq. 6:

Since L_s is intended to block the RF leakage to the ground, the L_s value of a conventional CG LNA is higher than that of a CS LNA, and the Q_cs value is higher than the Q_cg value. Obtaining a wideband input match and absorbing parasitic capacitances with a CG LNA is relatively simple, making this a suitable topology for UWB applications.

where:

V_th0 = the threshold voltage when V_bs = 0;

γ = the body-effect coefficient;

σ_f = the surface potential; and

V_bs = the voltage between the body and the source.

Usually, V_bs ≤ 0, so V_th ≥ V_th0. To reduce V_th, V_bs is set greater than zero so that V_th < V_th0. The typical value of V_th is about 0.5 V. For the proposed LNA design, V_bs = 0.29 V and V_th = 0.43 V.  

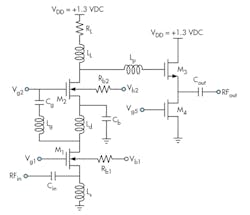
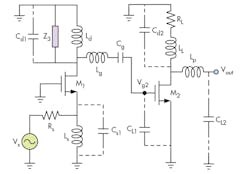
The UWB LNA was designed and simulated in a standard 0.18-μm RF CMOS process. Figure 3 shows a schematic diagram of the proposed LNA, including the output buffer stage (M₄, M₅). The current-reuse configuration can be considered as a two-stage cascade amplifier, where the first stage is the CG amplifier (M₁) and the second stage is the CS amplifier (M₂).

The signal amplified by M₁ is coupled to the gate of M₂ by series resonance (L_g and C_g) while the source of M₂ is bypassed by capacitor C_b. Besides, C_b determines the low-frequency band expansion and gain flatness. The circuit saves power through the reuse of the bias current.

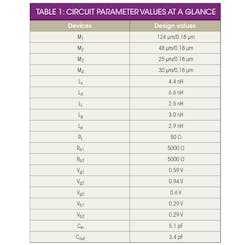
The CG topology LNA exhibits low power gain, so a CS amplifier is included in the second stage. It employs a gain peaking technique which consists of R_L, L_L, M₂, and L_p. To reduce the threshold voltage of the transistor, the forward body biasing is employed. The post-distortion technique is used in the first stage (M₃), reducing the nonlinearity of the main device (M₁). Table 1 summarizes the circuit parameters of the proposed LNA.

RF/microwave components and systems are typically designed for a standard impedance of 50 Ω, so the input stage of the UWB LNA should match to 50 Ω with minimal power reflection.²¹ For simplicity in this analysis, body effects are ignored. Figure 4 shows the CG input stage of the proposed UWB LNA, and the input impedance can be derived by Eq. 8:

where:

C_ta = the total capacitance at node a;

C_tb =  the total capacitance at node b;

C_gs1 = the gate-to-source capacitance;

g_m1 = the transconductance;

r₀₁ = the output resistance of M₁; and

Z_L = the CS stage equivalent load impedance.

As Eq. 8 indicates, the input impedance approximates 1/g_m1 over the frequency band of interest. Transconductance g_m3 << g_m2, where g_m2 and g_m3 are the transconductances of transistor M₂ and M₃, respectively. The input impedance Z_in(ω as seen from resistor R_s of the CG LNA is about the same with or without transistor M₃ present, so that M₃ cannot be considered to significantly affect the input impedance matching.

However, for a wideband input match, Eq. 8 indicates that g_m1 of M₁ in the CG stage should slightly exceed 20 mS. Through simulation, input matching is considered good when g_m1 approaches 26 mS.

The achievable maximum power gain also depends on the output impedance matching. In the proposed LNA, a simple source follower, which consists of M₄ and M₅, is employed to obtain output impedance matching. If the source of M₂ is perfectly grounded by C_b, the equivalent schematic of the proposed LNA can be redrawn in Fig. 5, where the proposed UWB LNA is created by the two-stage amplifier.

The first stage is a CG amplifier and the second stage is a CS amplifier. For simplicity, body effects are not considered. The voltage gain of the first stage, A_V1, can be expressed by Eq. 9:

where:

g_m1 = the transconductance of M₁;

r₀₁ = the channel resistance of M₁;

R_S = the input source resistance (50 Ω);

C_s1 = the source parasitic capacitance caused by C_gs1;

C_d1 = the drain parasitic capacitance caused by C_gd1;

C_L1 = the parasitic load capacitance of the second stage; and

Z₃ = the equivalent impedance of M3.

For simplicity’s sake, the direct-current (DC) blocking capacitors C_in and C_out are ignored in the analysis.

The voltage gain of the second-stage, A_V2, is given by Eq. 14:

g_m2, γ₀₂, and C_L2 are the transconductance of transistor M₂, the channel resistance of M₂, and the total load capacitance at the second-stage output, respectively. Additionally, C_d2 is the calculated parasitic capacitance at the drain of M₂, which is produced by the gate-to-drain parasitic capacitor (C_gd2). The overall circuit frequency response of S₂₁ has a good flatness and a high power gain because of the cascaded first and second stages.

which are produced by source resistor R_s and the channel noise of M₁, M₂, and load resistor R_L. Parameters k, T, γ, and Δf represent Boltzmann’s constant, the absolute temperature (in degrees Kelvin), the thermal noise coefficient (having a value from 1 to 2 in the saturation region of a short channel MOSFET), and the noise bandwidth (in Hz), respectively.

The noise factor of the proposed LNA can be expressed by Eq. 21:

where V_2n,out is the total noise at the output and AV is the total voltage gain.

The total voltage gain AV can be obtained by Eqs. 17 and 21. From Eq. 21, it can be seen that the effects of g_m1 and g_m2 can be seen on achieving a lower noise factor; for low noise and low power consumption, g_m1 should have a low value. But this can also have adverse effects on the total noise factor since low g_m1 leads to low first-stage gain.

Alternately, from Eq. 21, it can be seen that a high g_m2 value is beneficial for low noise factor, although the high value will also increase power dissipation. For best performance, the values of g_m1 and g_m2 should be optimized. Because both transconductance values depend on transistor width (W₁ and W₂, in the proposed LNA design, the optimal values of W₁ and W₂ are 124 and 48 μm, respectively.

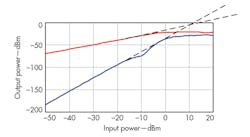
The proposed UWB LNA was designed and simulated with the aid of the Advanced Design System (ADS) software from Agilent Technologies (now Keysight Technologies), using a standard 0.18-μm silicon RF CMOS process. With current reuse and forward body biasing, the supply voltage is only +1.3 VDC and the power consumption is only 3.1 mW.

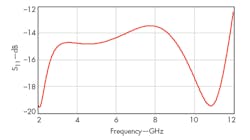
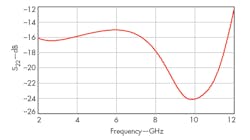
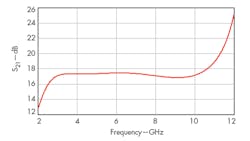
Figure 6 shows simulated input reflection coefficient (S₁₁, which is less than -13 dB from3 to 11 GHz. Figure 7 shows simulated output reflection coefficient (S₂₂), which is less than -14 dB from 3 to 11 GHz. Figure 8 shows voltage gain (S₂₁) for the LNA, which ranges from 16.8 to 18.9 from 3 to 11 GHz. As a result of a shunt-series peaking technique, S₂₁ shows high voltage gain with good flatness.

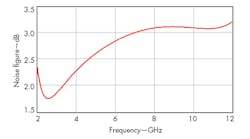
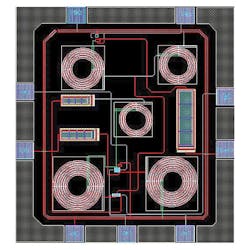
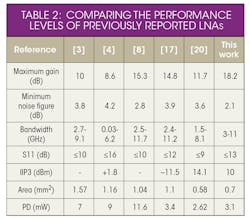
Figure 9 plots the noise figure of the proposed LNA, which ranges from 1.9 to 3.2 dB across 3 to 11 GHz. Figure 10 shows the layout of the proposed LNA, with total chip area of 0.87 × 0.81 mm², including the input and output pads. Table 2 summarizes its performance and compares it with previous work.

Acknowledgment

The authors would like to thank the research platform of the Open Fund Project for access to the coal mine monitoring network based on the wireless sensor networks in the Department of Education of Hunan Province, grant No. 12C0986.

Xu Xia, Professor

Hunan Vocational College of Security Technology, Changsha, 410151, Hunan Province, People’s Republic of China

Fengying Han, Professor

Changsha Aeronautical Vocational and Technical College, Changsha, 410014, Hunan Province, People’s Republic of China